2个回答
1
我想我懂了。
- 找到
x坐标最小的顶点。如果有多个,则选择y坐标最小的顶点。这个过程的时间复杂度是O(n)。 - 在与第一步中找到的顶点相连的 2 条或以上线段中,选择与 x 轴夹角最小的线段,以便按顺时针方向遍历多边形。这个过程的时间复杂度是
O(s),其中s是与起始顶点相连的线段数。 - 保持选择下一个相连的线段,忽略原始多边形中的线段顺序。如果出现交叉,则选择与当前线段逆时针方向夹角最小的线段,以便选择位于多边形外部的线段。这个过程的时间复杂度是
O(n i/2),其中i是每个顶点相连的平均线段数。 - 回到起点后,使用鞋带公式计算面积。在步骤 2 和 3 中遍历多边形时,实际上可以并行计算面积。
这个算法的最坏时间复杂度为 O(n i/2),其中 n 是顶点数,i 是每个顶点连接的平均线段数。当多边形不相交时,最佳情况的复杂度为 O(n)。在我的案例中,多边形很少相交,因此这个过程接近于 O(n)。
- satoshi
1
我认为这可能有效,看起来有点像我们研究过的 Graham 扫描算法。我会给你一票。 - Carlos
0
- 根据给定的点构建线段集
- 对于每个点,测试一条射线是否与这些线段相交了偶数次或奇数次。
- 偶数次相交计数是内部点,将其删除。
- Shoelace算法告诉你剩余形状的面积。
让我想一种不是n^2的方法,因为你要比较n个点和n个线段。
- Carlos
3
是的,谢谢你提供这个方案,这是我能想到的最好的方法,但正如你所说的“O(n²)”,并不理想... - satoshi
@satoshi 请考虑是否有用使用一个点(x,y),其中x和y都比集合中的最小值更低,即在集合的左下角,然后计算到所有点的角度,并进行nlogn排序。我还没有完全想清楚。 - Carlos
嗨@Carlos,是的,我一直在考虑类似于Graham扫描算法用于凸包的东西,但我无法完全适应它来解决我的问题。 - satoshi
网页内容由stack overflow 提供, 点击上面的可以查看英文原文,
原文链接
原文链接
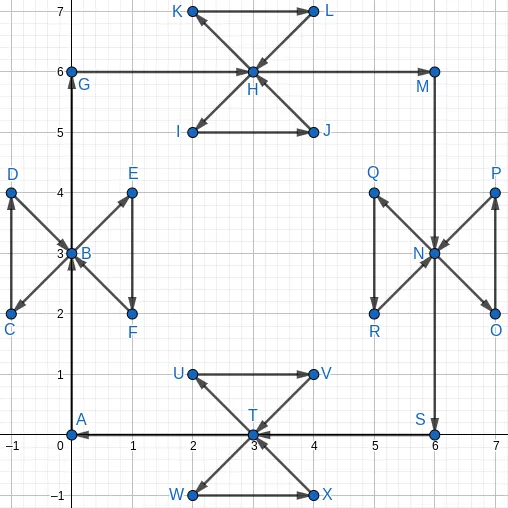
D->B,B->E... 一些顶点有多个入射线段(D&F->B),一些顶点有多个出射线段(B->C&E)。 - Reblochon Masque