问题是由于R的数值精度限制引起的。正如评论者所指出的那样,我计算的n个k值实在太大了(
choose(80,40) = 1.075072e+23)。
我们可以使用对数来尝试将问题保持在R的计算限制内。这是拉马努金方法的实现。不幸的是,近似误差会累积,并且精度下降得更快。概率函数需要添加和减去一系列非常大的数字,以获得介于0和1之间的最终值,并且不能容忍任何不精确性。
0)重写概率函数以分步进行
probability <- function(s, m, n) {
i <- 0:((s-1-n) / m)
c1 <- choose(n, i)
c2 <- choose(s - 1 - i * m, n)
seq <- (-1)^i * (c1 * c2)
m^(-n) * sum(seq)
}
1) 实现log(x!)的近似值
ramanujan <- function(n){
n * log(n) - n + log(n * (1 + 4*n * (1 + 2*n))) / 6 + log(pi) / 2
}
n <- 1:200
diff <- log(factorial(n)) - ramanujan(n)
plot(n, diff)
2) 使用对数逼近重写choose函数。
log_nck <- Vectorize(function(n, k) {
if(n <= k | n < 1 | k < 1) return(log(choose(n,k)))
return((ramanujan(n) - ramanujan(k) - ramanujan(n-k)))
})
n <- seq(10, 100, 10)
k <- seq(5, 50, 5)
c_real <- log(choose(n, k))
c_approx <- log_nck(n, k)
print(c_real)
print(c_approx)
print(c_real - c_approx)
3) 使用对数组合重写概率函数。
new_probability <- function(s, m, n) {
i <- 0:((s-1-n) / m)
c1 <- log_nck(n, i)
c2 <- log_nck(s - 1 - i * m, n)
seq <- (-1)^i * exp(c1 + c2)
return(m^(-n) * sum(seq))
}
最终测试
n <- 1:90
m <- 6
s <- floor(mean(1:m)*n)
p <- mapply(probability, s = s, m = m, n = n)
newp <- mapply(new_probability, s = s, m = m, n = n)
plot(n, p, main = "Original in black, approximation in red")
points(n, newp, col = "red")
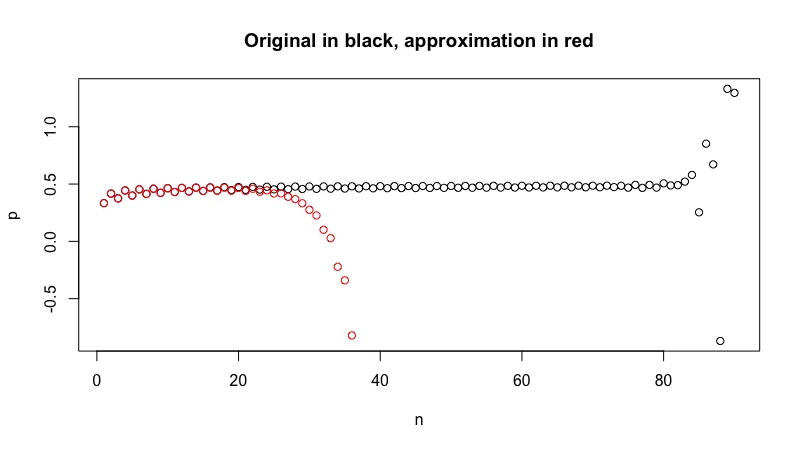
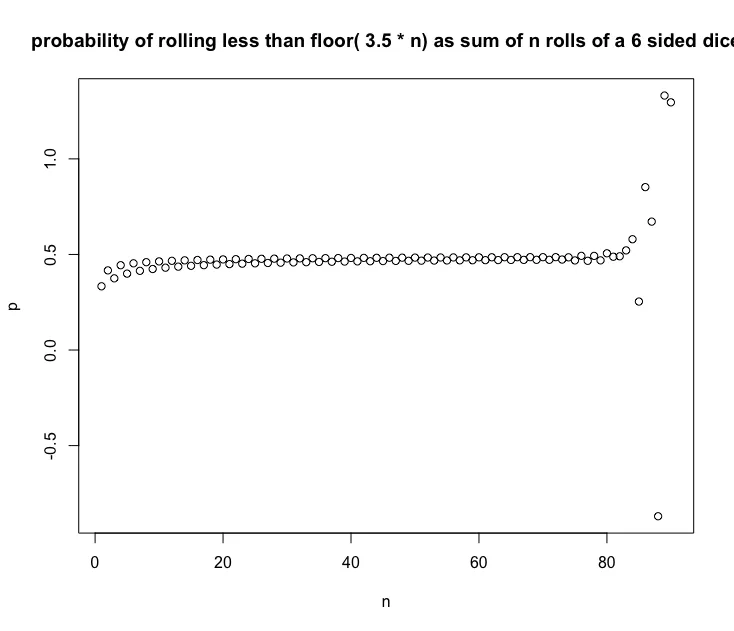
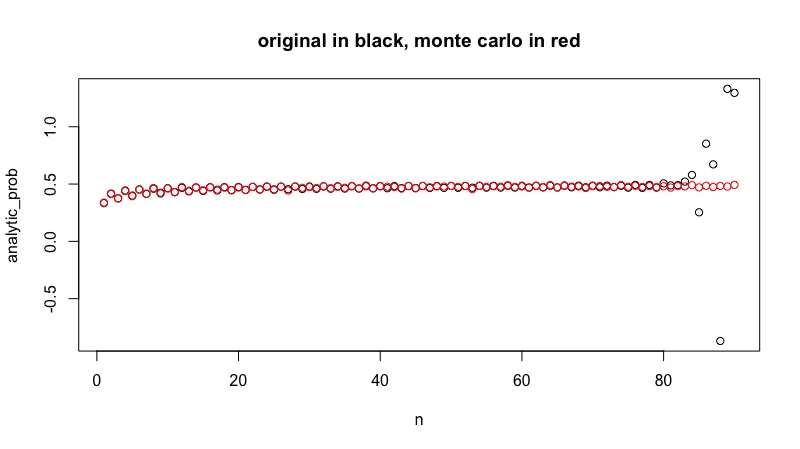

choose(80,40)。你的公式在数值上不稳定。也许尝试在对数尺度上计算会更好。 - MrFlickn很大时,choose会完全失去精度。也许你可以阅读 https://dev59.com/r1kR5IYBdhLWcg3w_CD-#40527881 以获取替代方案。 - ThomasIsCodingbase::choose处理小值的n和k时遇到了问题。我会编辑问题以包含我的进展。 - Lief Esbenshade