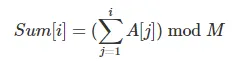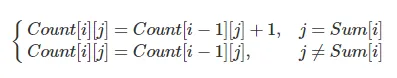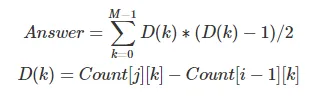高效算法以快速回答子数组查询

Question

前几天我遇到了一个与查询相关的问题，但我无法解决。

给定一个包含N个整数和一个正整数M的数组，您必须回答Q个查询。每个查询都表示为( i , j )，其中i和j是数组的索引。在每个查询中，您必须回答有多少对( r , s )满足以下条件:

1. i <= r <= s <= j
2. 具有指数在[ r , s ]之间的数组元素的总和可被M整除。

限制：

N <= 50,000
Q <= 50,000
M <= 100

我有一个动态规划的解决方案，它对每个查询（r，s）进行预处理，时间复杂度为O（N^2），但速度不够快。是否有更有效率的解决方案？我有一些使用莫队算法或线段树的想法，但是我无法实现。

- Diego Garcia

---

首先对数组进行排序（对数复杂度）。现在子范围（i，j）可以用二分搜索找到。为了计算给定的（i，j），需要预计算范围内模M的所有值以及每个值[0，M)出现的次数。根据每个值的数量，可以轻松地计算可能的配对数。 - Sam Varshavchik

@SamVarshavchik，“（i，j）”是数组的索引，而不是值。 - DAle

Answer 1

1. 计算原始数组的前缀和（假设从1开始）对于每个i = 1..N。
   
   当r < s时，Sum[r]和Sum[s]的等价性意味着索引在[r+1, s]范围内的数组元素之和可被M整除（我们需要在该区间内计算这样的等价性数量）。此步骤的时间复杂度为O(N)。
   
   

2. 预先计算数组Count，对于每个i = 1..N, j = 0..M-1：
   Count[i][j]存储了Sum[len]（其中len <= i）等于j的次数。此步骤的时间复杂度为O(N*M)。
   
   

3. 对于每个查询(i, j)，答案将等于：
   对于每个余数k的可能值，我们找到D(k) - 在区间[i, j]中Sum[len]等于k的次数。然后，我们将结果加上所有可能的D(k)区间边界的配对数量，即D(k)*(D(k)-1)/2。每个查询的时间复杂度为O(M)。
   
   

复杂度：O(N) + O(N*M) + O(Q*M) = O((Q+N)*M)，对于给定的限制条件来说是可以接受的。

- DAle

Answer 2

请注意，对于任何加和为 M 的子数组 (r, s)：

sum(r, s) == sum(i, s) - sum(i, r - 1)

          == (qa * M + ra) - (qb * M + rb)

其中ra和rb均小于M且大于等于0（即通过M取余后的相应余数）。

现在sum(r, s)可被M整除，因此通过M取余的余数为0。因此：

ra == rb

如果我们计算所有子数组 (i, i), (i, i + 1), ... ,(i, j) 对 M 取余后的余数，分别为 r1, r2, ... , rj，然后将所有这些余数的计数存储在大小为 M 的数组 R 中，使得 R[k] 是等于 k 的余数的数量，则：

R[0] == the number of subarrays starting at i that are divisible by M

对于每个 k >= 0 且 k < M，满足 R[k] > 1，我们可以计算 R[k] 选 2：

(R[k] * (R[k] - 1)) / 2

子数组不以i开头且可被M整除。

创建并求和所有这些值可以在每个(r, s)查询中以O(N+M)的时间复杂度得出答案。

- Paul Evans

---

为什么复杂度是 O(Q+M)？可能是 O(Q*M) 吗？ - DAle

@DAle 从 i 到 j 循环计算下一个累加和的余数并更新 R，需要 Q 步。然后需要 M 步循环遍历 R 并在每一步更新总和，时间复杂度为 O(Q+M)。 - Paul Evans

Q 是查询数量。 - DAle

@DAle 啊，你完全正确！已更新答案 - 谢谢。原始问题每个查询的时间复杂度为 O(N^2)，现在变成了 O(N+M)。 - Paul Evans