寻找最大平衡子数组的空间高效算法？

Question

给定一个由0和1组成的数组，找到最大子数组，使得其中的0和1的数量相等。需要在O(n)时间复杂度和O(1)空间复杂度内完成。

我有一个算法可以在O(n)时间复杂度和O(n)空间复杂度内实现。它使用了前缀和数组，并利用了这样一个事实，即如果0和1的数量相同，则子数组的和=sumOfSubarray = lengthOfSubarray/2

#include<iostream>
#define M 15

using namespace std;

void getSum(int arr[],int prefixsum[],int size) {
    int i;
    prefixsum[0]=arr[0]=0;
    prefixsum[1]=arr[1];
    for (i=2;i<=size;i++) {
        prefixsum[i]=prefixsum[i-1]+arr[i];
    }
}

void find(int a[],int &start,int &end) {
    while(start < end) {
        int mid = (start +end )/2;
        if((end-start+1) == 2 * (a[end] - a[start-1]))
                break;
        if((end-start+1) > 2 * (a[end] - a[start-1])) {
            if(a[start]==0 && a[end]==1)
                    start++; else
                    end--;
        } else {
            if(a[start]==1 && a[end]==0)
                    start++; else
                    end--;
        }
    }
}

int main() {
    int size,arr[M],ps[M],start=1,end,width;
    ;
    cin>>size;
    arr[0]=0;
    end=size;
    for (int i=1;i<=size;i++)
            cin>>arr[i];
    getSum(arr,ps,size);
    find(ps,start,end);
    if(start!=end)
            cout<<(start-1)<<" "<<(end-1)<<endl; else cout<<"No soln\n";
    return 0;
}

- vastutsav

---

我想知道如果你把零替换成负一，是否更容易做到这一点。这样子数组的总和就是零。 - Neil

我们可以修改原始数组吗？ - templatetypedef

由于这是一项作业，我们可以假设存在O（1）的存储解决方案吗？ - Paul Rubel

我怀疑这在O(1)空间内是不可能的。 - Tomas

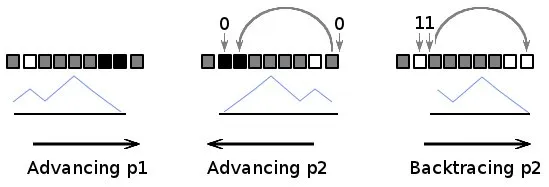
您发布的算法似乎有误。输入大小为4，数组数据为1、1、1、0，您会发现答案是无解的。原因在于if(a[start]==0 && a[end]==1)和if(a[start]==1 && a[end]==0)这两行代码。这里的a指的是前缀和数组；我相信您本意是引用原始数据。事实上，条件a[start]==1 && a[end]==0是不可能的；因为start < end且数组中没有负数元素，所以直到start的前缀和不能大于直到end的前缀和。 - Karthik Viswanathan

Answer 1

现在我的算法时间复杂度为O(n)，空间复杂度为O(Dn)，其中Dn是列表中的总不平衡量。

这个解决方案不会修改列表。

设D为列表中发现的1和0的差异。

首先，让我们线性地遍历列表并计算D，以查看它是如何工作的：

我将使用这个列表作为示例：l=1100111100001110

Element   D
null      0
1         1
1         2   <-
0         1
0         0
1         1
1         2
1         3
1         4
0         3
0         2
0         1
0         0
1         1
1         2
1         3
0         2   <-

找到最长平衡子数组等同于找到D中距离最远的2个相等元素。（在这个例子中，标有箭头的2个2。） 最长平衡子数组位于元素第一次出现+1和最后一次出现之间。（第一个箭头+1和最后一个箭头：00111100001110）

注意：

最长的子数组始终位于D中的两个元素之间，这些元素位于[0，Dn]之间，其中Dn是D的最后一个元素。(在前面的示例中，Dn = 2) Dn是列表中1和0之间的总不平衡度。(如果Dn为负，则为[Dn，0])

在此示例中，这意味着我不需要“查看”3或4。

证明：

让Dn > 0。

如果存在由P（P > Dn）限定的子数组。由于0 < Dn < P，在到达第一个等于P的D元素之前，我们会遇到一个等于Dn的元素。因此，由于列表的最后一个元素等于Dn，所以由Dns限定的最长子数组比由Ps限定的最长子数组更长。因此，我们不需要查看Ps

出于同样的原因，P不能小于0

Dn <0的情况下证明相同

现在我们来处理D，D不是随机的，相邻元素之间的差值始终为1或-1。而且D和初始列表之间有一个简单的双射关系。因此，我有两种解决方案：

• 第一种方法是跟踪0到Dn之间每个元素在D中的第一次和最后一次出现。
• 第二种方法是将列表转换为D，然后对D进行操作。

---

第一种解决方案

暂时我找不到比第一种更好的方法：

首先计算Dn（在O（n）内）。 Dn = 2

其次，不要创建D，而是创建一个字典，其中键是D的值（在[0和Dn]之间），每个键的值都是一对（a，b），其中a是键的第一次出现，b是最后一次出现。

Element   D DICTIONNARY
null      0 {0:(0,0)}
1         1 {0:(0,0) 1:(1,1)}
1         2 {0:(0,0) 1:(1,1) 2:(2,2)}
0         1 {0:(0,0) 1:(1,3) 2:(2,2)}
0         0 {0:(0,4) 1:(1,3) 2:(2,2)}
1         1 {0:(0,4) 1:(1,5) 2:(2,2)}
1         2 {0:(0,4) 1:(1,5) 2:(2,6)}
1         3 { 0:(0,4) 1:(1,5) 2:(2,6)}
1         4 {0:(0,4) 1:(1,5) 2:(2,6)}  
0         3{0:(0,4) 1:(1,5) 2:(2,6) }
0         2 {0:(0,4) 1:(1,5) 2:(2,9) }
0         1 {0:(0,4) 1:(1,10) 2:(2,9) } 
0         0 {0:(0,11) 1:(1,10) 2:(2,9) } 
1         1 {0:(0,11) 1:(1,12) 2:(2,9) } 
1         2 {0:(0,11) 1:(1,12) 2:(2,13)}
1         3 {0:(0,11) 1:(1,12) 2:(2,13)} 
0         2 {0:(0,11) 1:(1,12) 2:(2,15)} 

你选择了差异最大的元素：2:(2,15)，并且是l[3:15]=00111100001110（其中l=1100111100001110）。

时间复杂度：两次遍历，第一次计算Dn，第二次构建字典。在字典中查找最大值。总共为O(n)。

空间复杂度：D中的当前元素为O(1)，字典为O(Dn)。因为备注原因，我不将3和4加入字典中。

平均情况下，复杂度为O(n)时间和O(Dn)空间（Dn << n）。

我想这种方法可能有更好的方式而不是使用字典。

欢迎任何建议。

希望对你有所帮助。

---

第二种解决方案（只是一个想法而不是真正的解决方案）

第二种方法是将您的列表转换为D。（因为从D返回列表很容易，所以可以这样做）。 (O(n)时间和O(1)空间，因为我在原地转换列表，尽管它可能不是“有效”的O(1))

然后从D中找到两个相等的元素，它们之间的距离最远。

它看起来像是查找链表中最长循环的算法，Richard Brent algorithm 的修改版本可能会返回最长循环，但我不知道如何做，它需要O(n)时间和O(1)空间。

一旦找到最长循环，回到第一个列表并打印它。

该算法的时间复杂度为O(n)，空间复杂度为O(1)。

- Ricky Bobby

---

如果您需要转换列表，则它不是O(1)空间。 - Tomas

@Tomas T. 为什么这样？如果我就是在原地修改它怎么办？无论如何，我的第二种解决方案只是个想法，因为我还没有一个算法来查找链表中最长的循环。目前只有第一个能够运作，在O(n)的时间和O(M)的空间内，其中M << n并且是列表中最大的不平衡值。 - Ricky Bobby

我认为修改输入是不允许的，即转换输入列表不是O(1)空间。 - Tomas

我认为修改输入是允许的，但只能在输入空间内进行。当你用n次log n替换一个1位条目（或者使用任何你想要的常数，比如8位字符，都无所谓），并将其替换为最大可能的数字...，那么所需的空间就是O(n log n)。 - flolo

@flolo，你说得对，但在这种情况下，我甚至不能使用列表中任何元素的索引:D...无论如何（再次），我的第二个解决方案并不完整，我知道这一点，我只是写了它，因为它可能会指导某人找到正确的解决方案。但第一个解决方案有效，并且需要O(n)时间和O(M)空间（如果考虑到你的评论，则需要O(M*ln(M))）（其中M是最大不平衡度，在平均情况下M<<n）。 - Ricky Bobby

Answer 2

不同的方法，但仍是O(n)的时间和内存。从Neil的建议开始，将0视为-1。

符号说明：A [0，...，N-1] - 大小为N的数组，f（0）= 0，f（x）= A[x-1] + f（x-1） - 一个函数

如果您绘制f，您会发现，您要查找的是使f(m)= f(n)，其中m = n-2k，其中k为正自然数的点。更准确地说，只有对于x，使A[x]!= A[x + 1]（以及数组中的最后一个元素），您必须检查是否已经出现了f(x)。不幸的是，现在我看不到比拥有数组B [- N + 1 ... N-1]更好的改进，在其中存储此类信息。

为了完成我的想法： B [x] = -1 初始值，当p = min k：f（k）= x 时， B [x] = p 。算法是（请仔细检查，因为我非常累）：

fx = 0
B = new array[-N+1, …, N-1]
maxlen = 0
B[0]=0
for i=1…N-1 :
    fx = fx + A[i-1]
    if B[fx]==-1 :
        B[fx]=i
    else if ((i==N-1) or (A[i-1]!=A[i])) and (maxlen < i-B[fx]):
        We found that A[B[fx], …, i] is best than what we found so far
        maxlen = i-B[fx]

---

编辑：两个床上想法（=躺在床上想出来的 :P）：

1） 你可以通过子数组长度二分搜索结果，这将得到O(n log n)时间和O(1)内存算法。让我们使用函数g(x)=x - x mod 2（因为总和为0的子数组总是偶数长度）。首先检查整个数组是否总和为0。如果是--我们完成了，否则继续。现在我们将0假定为起点（我们知道有这样长度的子数组并且具有“总和为零属性”），将g(N-1)作为终点（我们知道没有这样的子数组）。让我们执行

    a = 0
    b = g(N-1)
    while a<b : 
        c = g((a+b)/2)
        check if there is such subarray in O(n) time
        if yes:
            a = c
        if no:
            b = c
    return the result: a (length of maximum subarray)

检查长度为L的子数组是否具有“零和”属性很简单:

    a = 0
    b = L
    fa = fb = 0
    for i=0…L-1:
        fb = fb + A[i]
    while (fa != fb) and (b<N) :
        fa = fa + A[a]
        fb = fb + A[b]
        a = a + 1
        b = b + 1
    if b==N:
        not found
    found, starts at a and stops at b

2) …你能修改输入数组吗？如果可以，且O(1)内存确切意味着你不使用额外的空间（除了常数个元素），那么只需将前缀表值存储在输入数组中即可，不再使用更多的空间（除了一些变量）:D

再次检查我的算法，因为我很累可能会出现差一错误。

- kgadek

Answer 3

像Neil一样，我发现考虑字母表{±1}而不是{0,1}很有用。不失一般性地假设+1的数量至少与-1相同。下面的算法由“A.F.”提出，它使用O(sqrt(n log n))位并在O(n)时间内运行。 注意：此解决方案没有作弊，因为它假设输入是可修改的和/或具有浪费的位。截至本编辑时，这个解决方案是发布的唯一一个既是O(n)时间又是o(n)空间的解决方案。 一个更简单的版本，使用O(n)位，流式传输前缀和数组并标记每个值的第一次出现。然后向后扫描，在考虑高度为0到sum(arr)之间的每个高度时，找到该高度下的最大子数组。一些思考揭示了最佳解在其中（记住假设）。在Python中实现如下：

sum = 0
min_so_far = 0
max_so_far = 0
is_first = [True] * (1 + len(arr))
for i, x in enumerate(arr):
    sum += x
    if sum < min_so_far:
        min_so_far = sum
    elif sum > max_so_far:
        max_so_far = sum
    else:
        is_first[1 + i] = False

sum_i = 0
i = 0
while sum_i != sum:
    sum_i += arr[i]
    i += 1
sum_j = sum
j = len(arr)
longest = j - i
for h in xrange(sum - 1, -1, -1):
    while sum_i != h or not is_first[i]:
        i -= 1
        sum_i -= arr[i]
    while sum_j != h:
        j -= 1
        sum_j -= arr[j]
    longest = max(longest, j - i)

将英文翻译成中文：

将空间降低的技巧在于注意到我们按顺序扫描is_first，尽管相对于其构造是倒序的。由于循环变量适合O(log n)位，因此我们将计算每个O(√(n log n))步骤后的循环变量的检查点，而不是is_first。这是O(n/√(n log n)) = O(√(n/log n))个检查点，总共需要O(√(n log n))位。通过从检查点重新启动循环，我们按需计算每个O(√(n log n))位的is_first部分。

（附言：可能是我导致了问题陈述要求O(1)的空间复杂度。如果是我像费马一样建议我有一个比我想象的难得多的问题的解决方案，我真诚地道歉。）

- the guy formerly known as d

Answer 4

如果您的算法确实在所有情况下都有效（请参见我对您的问题的评论，指出其中一些更正），请注意前缀数组是实现您恒定内存目标的唯一障碍。

检查“find”函数会发现，该数组可以用两个整数替换，从而消除对输入长度的依赖并解决您的问题。考虑以下内容：

- 您在“find”函数中仅依赖于前缀数组中的两个值。这些值是“a [start-1]”和“a [end]”。是的，“start”和“end”会改变，但这是否值得使用数组？ - 查看循环的进展。最后，“start”增加或“end”减少“仅一个”。 - 考虑上述语句，如果您将“a [start-1]”的值替换为整数，您将如何更新它的值？换句话说，在每个更改“start”的转换中，您可以做些什么来相应地更新整数以反映“a [start-1]”的新值？ - 这个过程可以重复进行“a [end]”吗？ - 如果实际上“a [start-1]”和“a [end]”的值可以用两个整数反映，那么整个前缀数组不再有任何作用了吗？因此，它不能被删除？

没有前缀数组的需求，所有存储依赖于输入长度的算法都将使用恒定的内存量来实现其目标，从而使其时间复杂度为O（n），空间复杂度为O（1）。

基于上述见解，我希望您自己解决这个问题，因为这是作业。尽管如此，我已经包含了下面的解决方案供参考：

#include <iostream>
using namespace std;

void find( int *data, int &start, int &end )
{
    // reflects the prefix sum until start - 1
    int sumStart = 0;

    // reflects the prefix sum until end
    int sumEnd = 0;
    for( int i = start; i <= end; i++ )
        sumEnd += data[i];

    while( start < end )
    {
        int length = end - start + 1;
        int sum = 2 * ( sumEnd - sumStart );

        if( sum == length )
            break;
        else if( sum < length )
        {
            // sum needs to increase; get rid of the lower endpoint
            if( data[ start ] == 0 && data[ end ] == 1 )
            {
                // sumStart must be updated to reflect the new prefix sum
                sumStart += data[ start ];
                start++;
            }
            else
            {
                // sumEnd must be updated to reflect the new prefix sum
                sumEnd -= data[ end ];
                end--;
            }
        }
        else
        {
            // sum needs to decrease; get rid of the higher endpoint
            if( data[ start ] == 1 && data[ end ] == 0 )
            {
                // sumStart must be updated to reflect the new prefix sum
                sumStart += data[ start ];
                start++;
            }
            else
            {
                // sumEnd must be updated to reflect the new prefix sum
                sumEnd -= data[ end ];
                end--;
            }
        }
    }
}

int main() {
    int length;
    cin >> length;

    // get the data
    int data[length];
    for( int i = 0; i < length; i++ )
        cin >> data[i];

    // solve and print the solution
    int start = 0, end = length - 1;
    find( data, start, end );

    if( start == end )
        puts( "No soln" );
    else
        printf( "%d %d\n", start, end );

    return 0;
}

- Karthik Viswanathan

Answer 5

这个算法的时间复杂度为O(n)，空间复杂度为O(1)。它可以修改源数组，但会还原所有信息，因此无法处理const类型数组。如果这个谜题有多个解决方案，该算法将选择最接近数组开头的解决方案。或者可以修改该算法以提供所有解决方案。

算法

变量：

• p1 - 子数组起始位置
• p2 - 子数组结束位置

• d - 子数组中1和0的差异

  1. 计算 d，如果 d==0，则停止。如果 d<0，则反转数组，并在找到平衡子数组后再次反转。
  2. 当 d > 0 时，前进 p2：如果数组元素为1，则只需将 p2 和 d 都减少1。否则，p2 应通过形式为 11*0 的子数组，其中 * 是某个平衡子数组。为了使回溯成为可能，11*0? 被更改为 0?*00（其中 ? 是子数组旁边的值）。然后将 d 减1。
  3. 存储 p1 和 p2。
  4. 回溯 p2：如果数组元素为1，则只需将 p2 增加1。否则，我们发现了第2步更改的元素。恢复更改并通过形式为 11*0 的子数组。
  5. 前进 p1：如果数组元素为1，则只需将 p1 增加1。否则，p1 应通过形式为 0*11 的子数组。
  6. 如果 p2 - p1 改善，则存储 p1 和 p2。
  7. 如果 p2 在数组末尾，则停止。否则继续进行第4步。

它是如何工作的

算法遍历输入数组中平衡子数组的所有可能位置。对于每个子数组位置，p1和p2尽可能远离彼此，提供局部最长的子数组。在所有这些子数组之间选择具有最大长度的子数组。

为了确定p1的下一个最佳位置，它被推进到第一个平衡1和0之间差异增加1的位置。（步骤5）。

为了确定p2的下一个最佳位置，它被推进到最后一个平衡1和0之间差异增加1的位置。为了实现这一点，步骤2检测从数组末尾开始的所有这样的位置，并以这样的方式修改数组，使得可以通过线性搜索遍历这些位置。（步骤4）。

在执行第2步时，可能会遇到两种情况。简单情况是当找到值为“1”时，指针p2只需向前移动到下一个值，无需特殊处理。但是当找到值为“0”时，平衡方向出现错误，需要通过多个位来寻找正确的平衡。所有这些位对算法没有任何意义，在那里停止p2将给出一个平衡子数组，该数组太短，或者一个不平衡的子数组。因此，p2应通过形式为11*0（从右向左，*表示任何平衡的子数组）的子数组。没有机会以相反的方向走同样的路线。但是可以临时使用11*0模式中的一些位来实现回溯。如果我们将第一个“1”更改为“0”，将第二个“1”更改为最右侧“0”的旁边值，并清除最右侧“0”旁边的值：11*0？ -> 0？*00，那么我们就有了在回程途中（首先）注意到模式的可能性，因为它以“0”开头，以及（第二）找到下一个适合p2的好位置的可能性。

C++代码：

#include <cstddef>
#include <bitset>

static const size_t N = 270;

void findLargestBalanced(std::bitset<N>& a, size_t& p1s, size_t& p2s)
{
    // Step 1
    size_t p1 = 0;
    size_t p2 = N;
    int d = 2 * a.count() - N;
    bool flip = false;

    if (d == 0) {
        p1s = 0;
        p2s = N;
        return;
    }

    if (d < 0) {
        flip = true;
        d = -d;
        a.flip();
    }

    // Step 2
    bool next = true;
    while (d > 0) {
        if (p2 < N) {
            next = a[p2];
        }

        --d;
        --p2;

        if (a[p2] == false) {
            if (p2+1 < N) {
                a[p2+1] = false;
            }

            int dd = 2;
            while (dd > 0) {
                dd += (a[--p2]? -1: 1);
            }

            a[p2+1] = next;
            a[p2] = false;
        }
    }

    // Step 3
    p2s = p2;
    p1s = p1;

    do {
        // Step 4
        if (a[p2] == false) {
            a[p2++] = true;
            bool nextToRestore = a[p2];
            a[p2++] = true;

            int dd = 2;
            while (dd > 0 && p2 < N) {
                dd += (a[p2++]? 1: -1);
            }

            if (dd == 0) {
                a[--p2] = nextToRestore;
            }
        }
        else {
            ++p2;
        }

        // Step 5
        if (a[p1++] == false) {
            int dd = 2;
            while (dd > 0) {
                dd += (a[p1++]? -1: 1);
            }
        }

        // Step 6
        if (p2 - p1 > p2s - p1s) {
            p2s = p2;
            p1s = p1;
        }
    } while (p2 < N);

    if (flip) {
        a.flip();
    }
}

- Evgeny Kluev

---

我是不是理解错了，还是你的代码在以下示例中失败了？1100111100001110 1000110100011 应该分别产生(2,15) (3,12)。此外，我已经反复阅读了您的描述十几次，但我无法理解它。能否用不那么算法详细的方式描述一下主要思想？特别是第二步很混乱。据我所知，您会更改原始数组以创建110或000模式，这些模式表示(*)之间数组的某些特定属性？看起来不是一个好主意。 - Dmitri K

@wf34：很可能你没有考虑到这段代码片段中使用的位集使用从右到左的索引。此外，它报告的结果是半开区间，典型的C ++风格。只是一个主要概念？ - 这篇名为“它是如何工作的”的帖子的一部分，恰好是为了解释一个主要概念。第2步很混乱 - 对此感到抱歉，但如果说明中有什么不清楚的地方，您可以阅读代码。 - Evgeny Kluev

Answer 6

我有一个算法在O(n)时间和O(1)空间内运行。

它利用了简单的“缩小然后扩展”的技巧。代码中有注释。

public static void longestSubArrayWithSameZerosAndOnes() {
    // You are given an array of 1's and 0's only.
    // Find the longest subarray which contains equal number of 1's and 0's
    int[] A = new int[] {1, 0, 1, 1, 1, 0, 0,0,1};
    int num0 = 0, num1 = 0;

    // First, calculate how many 0s and 1s in the array
    for(int i = 0; i < A.length; i++) {
        if(A[i] == 0) {
            num0++;
        }
        else {
            num1++;
        }
    }
    if(num0 == 0 || num1 == 0) {
        System.out.println("The length of the sub-array is 0");
        return;
    }

    // Second, check the array to find a continuous "block" that has
    // the same number of 0s and 1s, starting from the HEAD and the
    // TAIL of the array, and moving the 2 "pointer" (HEAD and TAIL)
    // towards the CENTER of the array
    int start = 0, end = A.length - 1;
    while(num0 != num1 && start < end) {
        if(num1 > num0) {
            if(A[start] == 1) {
                num1--; start++;
            }
            else if(A[end] == 1) {
                num1--; end--;
            }
            else {
                num0--; start++;
                num0--; end--;
            }
        }
        else if(num1 < num0) {
            if(A[start] == 0) {
                num0--; start++;
            }
            else if(A[end] == 0) {
                num0--; end--;
            }
            else {
                num1--; start++;
                num1--; end--;
            }
        }
    }
    if(num0 == 0 || num1 == 0) {
        start = end;
        end++;
    }

    // Third, expand the continuous "block" just found at step #2 by
    // moving "HEAD" to head of the array and "TAIL" to the end of
    // the array, while still keeping the "block" balanced(containing
    // the same number of 0s and 1s
    while(0 < start && end < A.length - 1) {
        if(A[start - 1] == 0 && A[end + 1] == 0 || A[start - 1] == 1 && A[end + 1] == 1) {
            break;
        }
        start--;
        end++;
    }
    System.out.println("The length of the sub-array is " + (end - start + 1) + ", starting from #" + start + " to #" + end);

}

- Lianqi Li

Answer 7

这里有一个 ActionScript 的解决方案，看起来像是 O(n) 级别的缩放。虽然可能更像是 O(n log n)。但它绝对只使用了 O(1) 的内存。

警告 我没有检查它的完整性。我可能会漏掉一些情况。

protected function findLongest(array:Array, start:int = 0, end:int = -1):int {
    if (end < start) {
        end = array.length-1;
    }

    var startDiff:int = 0;
    var endDiff:int = 0;
    var diff:int = 0;
    var length:int = end-start;
    for (var i:int = 0; i <= length; i++) {
        if (array[i+start] == '1') {
            startDiff++;
        } else {
            startDiff--;
        }

        if (array[end-i] == '1') {
            endDiff++;
        } else {
            endDiff--;
        }

        //We can stop when there's no chance of equalizing anymore.
        if (Math.abs(startDiff) > length - i) {
            diff = endDiff;
            start = end - i;
            break;
        } else if (Math.abs(endDiff) > length - i) {
            diff = startDiff;
            end = i+start;
            break;
        }
    }

    var bit:String = diff > 0 ? '1': '0';
    var diffAdjustment:int = diff > 0 ? -1: 1;

    //Strip off the bad vars off the ends.
    while (diff != 0 && array[start] == bit) {
        start++;
        diff += diffAdjustment;
    }

    while(diff != 0 && array[end] == bit) {
        end--;
        diff += diffAdjustment;
    }

    //If we have equalized end. Otherwise recurse within the sub-array.
    if (diff == 0)
        return end-start+1;
    else
        return findLongest(array, start, end);      

}

- Jacob Eggers

---

递归需要栈-如果栈大小不是O(1)，那么你就没有O(1)的空间解决方案。 - Tomas

Answer 8

将数组中的所有元素相加，然后 diff = (array.length - sum)，它是 0 和 1 数量的差异。

1. 如果 diff 等于 array.length/2，则最大子串为数组本身。
2. 如果 diff 小于 array.length/2 则 1 的数量比 0 多。
3. 如果 diff 大于 array.length/2，则 0 的数量比 1 多。

对于情况 2 和 3，初始化两个指针，开始和结束分别指向数组的开头和结尾。如果我们有更多的 1，则根据 array[start] = 1 或 array[end] = 1 移动指针（start++ 或 end--），并相应地更新 sum。在每一步检查是否满足 sum = (end - start) / 2。如果这个条件成立，那么 start 和 end 就代表了最大子串的边界。

在这里，我们需要对数组进行两次遍历，一次计算 sum，一次移动指针。我们只需存储 sum 和两个索引值，因此使用的空间是恒定的。

如果有人想要写一些伪代码，欢迎参与 :)

- Oceanic

---

你能更准确地解释如何移动指针吗？我不明白你是如何决定移动哪个指针的。 也许你可以给出一个数组的例子（例如001000111011000001000之类的）。实际上，你使用了一种贪心算法，我不相信它在一般情况下都有效。 - kgadek

@kgadek，你应该努力减少差异。如果是情况（2），则测试任一侧是否为“1”（如果两侧都是，则选择一侧，比如左侧），并增加该侧的值；如果两侧都不是“1”，则选择一侧（比如左侧）并增加该侧的值。对于情况（3），行为相反。 - Mark Elliot

@Ricky：你需要始终选择一个方向，比如在你的情况下 0011 和 1100 都是有效的解决方案，选择左边将会增加左指针以得到 1100，选择右边则会得到 0011。 - Mark Elliot

жҜ”Oceanicе’ҢMarkжүҖжҡ—зӨәзҡ„иҰҒжӣҙеҠ еӨҚжқӮгҖӮдҪ еҸҜд»ҘиҪ»жҳ“жүҫеҮәе®ғдёҚйҖӮз”Ёзҡ„дҫӢеӯҗгҖӮ - Nitin Garg

@Mark：对于00011111111100，我该如何选择左侧或右侧？ - Ricky Bobby

-1. 1) 你的解决方案不起作用。2) 在你的第一段中，差分公式显然是错误的，应该是diff = 2 * sum - length。 - Tomas

Answer 9

我认为不存在时间复杂度为O(1)的算法，理由如下。假设你需要遍历每一位，这就需要一个计数器，其空间复杂度为O(log n)。有人可能会说n本身是问题实例的一部分，那么对于长度为k的二进制字符串，输入长度为k+2-log k。无论如何，你都需要一个额外的变量，以便在数组中进行索引，这已经使它不再是O(1)了。

通常情况下，你不会遇到这个问题，因为对于大小为n的问题，你会有n个大小为log k的数字作为输入，总共为nlog k。在这种情况下，长度为log k的变量只是O(1)。但是在这里，我们的log k只有1。因此，我们只能引入一个帮助变量，其长度是恒定的（我指的是真正的恒定，无论n有多大，它都必须受限）。

这里一个问题是问题描述变得明显了。在计算机理论中，你必须非常小心地选择编码方式。例如，如果你切换到一元编码，NP问题就可以变成多项式问题（因为此时输入大小比n元（n>1）编码要大得多）。

关于输入的n仅具有大小2-log n，我们必须小心。当你在这种情况下谈论O(n)时，实际上是一个O(2^n)的算法（这不是我们需要讨论的重点，因为人们可以争论n本身是否是描述的一部分）。

- flolo

---

虽然我理解你的意思，但是如果你假设机器是transdichotomous（大多数机器都是这样），那么你可以假设每个机器字可以容纳Omega(log n)位。在这种情况下，你可以使用O(1) 机器字来保存问题的大小。 - templatetypedef

@templatetypedef: 我不确定您想要表达什么意思。没错，您可以使用允许您在O(1)中表示问题的RAM模型。但这并没有说明什么。当您现在想要O（1）空间时，几乎总是可以实现的。我会说，已经呈现的每个算法都具有能力，即当您输入一个固定大小的问题时，答案可以在恒定（即O(1)）的空间中计算。顺便说一句，如果我考虑一下，输入适合于O(1)机器字也不太正确——例如n=256将意味着8位字，但您不能在一个8位字中存储256个元素（位）。 - flolo

Answer 10

线性时间，常数空间。如果我漏掉了任何错误，请告诉我。
在Python3中进行了测试。

def longestBalancedSubarray(A):
    lo,hi = 0,len(A)-1
    ones = sum(A);zeros = len(A) - ones
    while lo < hi:
        if ones == zeros: break
        else:
            if ones > zeros:
                if A[lo] == 1: lo+=1; ones-=1
                elif A[hi] == 1: hi+=1; ones-=1
                else: lo+=1; zeros -=1
            else:
                if A[lo] == 0: lo+=1; zeros-=1
                elif A[hi] == 0: hi+=1; zeros-=1
                else: lo+=1; ones -=1
    return(A[lo:hi+1])

- rnbguy