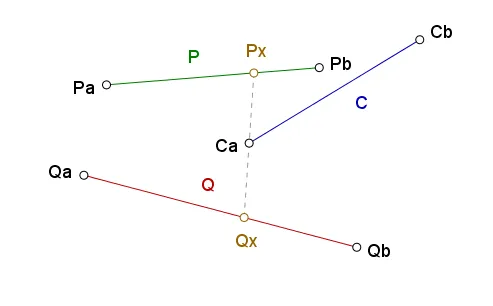
Px = P(t1) = Pa · (1 - t1) + Pb · t1
Qx = Q(t2) = Qa · (1 - t2) + Qb · t2
将"How do you detect where two line segments intersect?"中的方程式用于计算:
t(t1, t2) = (Ca - Px) ⨯ (Cb - Ca) / (Qx - Px) ⨯ (Cb - Ca)
u(t1, t2) = (Ca - Px) ⨯ (Qx - Px) / (Qx - Px) ⨯ (Cb - Ca)
(⨯ = 叉积)
这两个值必须在0和1之间,才能使线段相交。 t是沿着线Px Qx的位置,u是沿着C线的位置。如果您展开公式,它们将是两个线性或二次函数的商。
由于您只需要将t和u与零和一进行比较,因此它们可以稍微简化:
t(t1, t2) = 0
当且仅当 (Ca - Px) ⨯ (Cb - Ca) / (Qx - Px) ⨯ (Cb - Ca) = 0 且 (Ca - Px) ⨯ (Cb - Ca) = 0,其中Qx ≠ Px
和
t(t1, t2) = 1
当且仅当 (Ca - Px) ⨯ (Cb - Ca) / (Qx - Px) ⨯ (Cb - Ca) = 1 且 (Ca - Px) ⨯ (Cb - Ca) - (Qx - Px) ⨯ (Cb - Ca) = 0 且 (Ca - Qx) ⨯ (Cb - Ca) = 0,其中Qx ≠ Px
和
u(t1, t2) = 0
当且仅当 (Ca - Px) ⨯ (Qx - Px) / (Qx - Px) ⨯ (Cb - Ca) = 0 且 (Ca - Px) ⨯ (Qx - Px) = 0,其中Qx ≠ Px
u(t1, t2) = 1
(Ca - Px) ⨯ (Qx - Px) / (Qx - Px) ⨯ (Cb - Ca) = 1
(Ca - Px) ⨯ (Qx - Px) - (Qx - Px) ⨯ (Cb - Ca) = 0
(Ca - Px) ⨯ (Qx - Px) + (Cb - Ca) ⨯ (Qx - Px) = 0
(Cb - Px) ⨯ (Qx - Px) = 0, Qx ≠ Px
这里有四个约束条件(或者说八个,具体看你如何计算):
- 0 ≤ t1 ≤ 1
- 0 ≤ t2 ≤ 1
- 0 ≤ t(t1, t2) ≤ 1
- 0 ≤ u(t1, t2) ≤ 1
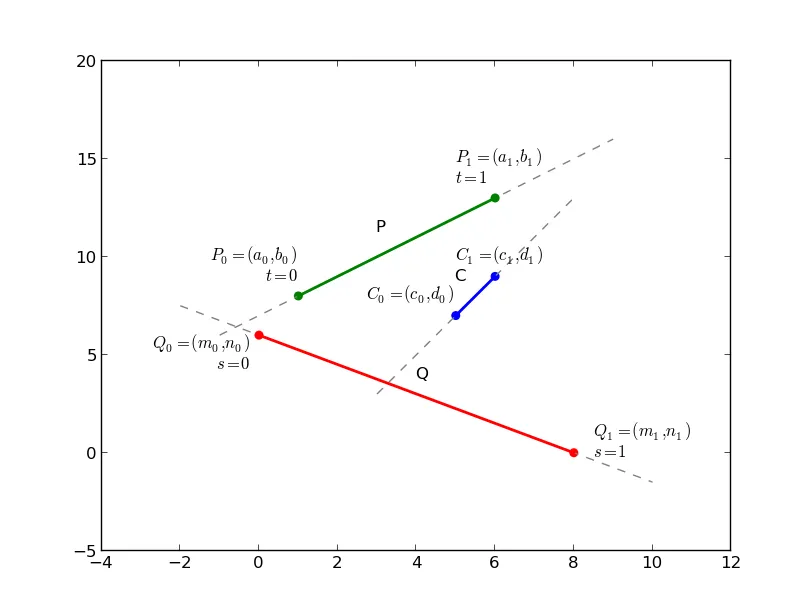
你有四个受约束的变量,每个变量都有两个边界。这样一来,在(t1, t2)空间中就会形成八种情况,每种情况代表着一个曲线或线段。
这些约束条件将形成一个在(t1, t2)空间中允许的值域。你需要沿着该区域的边缘寻找最小化Px和Qx之间距离的点。只要线段P和Q不相交,最小值总是位于外部边界上。但是在某些情况下,可能没有有效的解决方案。
为了找到最小值(t1, t2),你需要评估所有候选点:
- 内部最小值; 线P和Q相交的点。(1个点)
- 边界最小值; 沿任何边界曲线的最小值。(8个点)
- 交点最小值; 任意两个边界曲线相交的点。(24个点)
对于每个点,您需要检查它是否符合所有其他约束条件,并选择生成 Px 和 Qx 最小距离的点。
要找到内部最小点,请解决 Px = Py 的方程,得出 t1,t2。如果此点落在其他边界内,则直线相交并通过 C 线。(非常不可能)
要找到边界最小点,您需要查看曲线沿斜率。这可以通过解决以下问题找到:
{
∇f(t1, t2) ⨯ ∇G(t1, t2) = 0,
G(t1, t2) = k
}
其中 ∇ 是Nabla运算符(函数的一阶导数向量),G(t1, t2) = k 是边界条件,例如 t(t1, t2) = 1。
要找到交点最小值,您需要使两条曲线相等,并解决 t1,t2 的方程。
一种组织方法是计算每个约束曲线的多项式系数,并编写一个检查交点的函数。
(A1 + A2·t1 + A3·t12 + A4·t2 + A5·t1·t2 + A6·t22) / (A7 + A8·t1 + A9·t2)
 我们可以通过
我们可以通过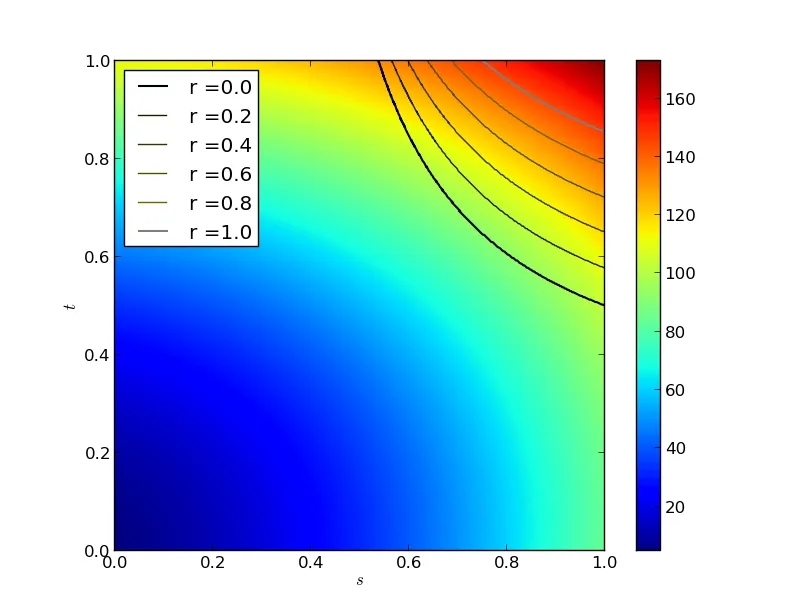 对于我们图中的特殊情况,随着的增加,等高线也会增加,其中和的等高线形成可行区域的边界。绘图中的底色是的值。更一般地说,具有额外约束条件的可行区域(即可能是问题的解的值)是位于框之间的和等高线之间的点。当然,可能没有等高线与框相交,此时要么整个框都是可行的,要么就没有解。与以前一样,除非和在可行区域内相交,否则最小值将出现在边界上。
对于我们图中的特殊情况,随着的增加,等高线也会增加,其中和的等高线形成可行区域的边界。绘图中的底色是的值。更一般地说,具有额外约束条件的可行区域(即可能是问题的解的值)是位于框之间的和等高线之间的点。当然,可能没有等高线与框相交,此时要么整个框都是可行的,要么就没有解。与以前一样,除非和在可行区域内相交,否则最小值将出现在边界上。
Ca,即两条线段(在上图中向左)的交点最近的点吗?因此,从所有通过Ca的线中找到与段内的2条线相交的交点,并将长度PxQx最小化。 - John Alexiou