Julia - 复数变量的优化

Question

我正在尝试解决一个简单的优化问题，我们希望将一个复数域的厄米矩阵作为变量（主题是量子力学）。

using Convex  #load the optimization solvers
using SCS

# define pauli-y+ projector
# by construction a positive operator valued hermitian matrix
y_plus = [1,im]/sqrt(2)
My0 = y_plus*y_plus'

# define the variable; a 2x2 density matrix
rho = Variable(2, 2)
problem.constraints += [rho == rho']     # hermitian
problem.constraints += [trace(rho) == 1] # unit trace
problem.constraints += [rho in :SDP]     # positive definite


# define the objective
problem = maximize(trace(rho*My0))

# solve
solve!(problem,SCSSolver(verbose=false))

problem.optval

问题是，当涉及到

时，Julia/JuMP/Convex.jl全部会出现错误。

maximize(trace(rho*My0))

由于 rho*My0 的迹原则上可以是复数，但是我们应该确保在给定 rho 和 My0 的约束条件下，rho*My0 是实数。

如何解决这些问题？可能有一个简单的解决方案。最坏的情况下，我们可能需要拆分实部和虚部。

- Willem Hekman

---

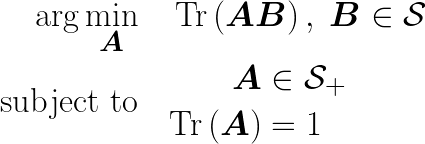
鉴于为代码夏季项目申请者添加复杂支持是一个开放的项目，你正处于支持行为的边缘。你可以尝试类似于maximize(trace(convert(Array{Float64}, rho*My0)))或者maximize(trace(real(rho*My0)))这样的方法，但我会对其是否有效感到惊讶。 - undefined

为什么不直接最大化abs(trace(rho*My0)))呢？如果迹是实数，那就一样了。 - undefined

@DanGetz，如果最大值是负数怎么办？abs()难道不意味着会得到最小值吗？在这种情况下，My0和rho都是半正定矩阵，因此它们的乘积的迹总是正的（https://math.stackexchange.com/questions/888677），所以在这种情况下这将起作用。但在这些条件下并不适用于任意两个矩阵。 - undefined

此外，我认为它不符合DCP的条件。 - undefined

Answer 1

你可以将问题写成以下形式： $$ \begin{align*} \arg \min_{\boldsymbol{A}} \quad & \operatorname{Tr} \left( \boldsymbol{A} \boldsymbol{B} \right), ; \boldsymbol{B} \in \mathcal{S} \ \text{subject to} \quad & \begin{aligned} \boldsymbol{A} & \in \mathcal{S}_{+} \ \operatorname{Tr} \left( \boldsymbol{A} \right ) & = 1 \end{aligned} \end{align*} $$

集合是对称正半定矩阵的集合。

这些问题是等价的，因为你可以始终使用 $\boldsymbol{B} = -\boldsymbol{M}$，根据你上面的问题。

投影步骤有3个：

1. 投影到对称矩阵集合。
2. 投影到正半定矩阵集合。
3. 投影到迹为单位的矩阵集合。

由于每个集合的投影都是已知的，我们可以很容易地解决这个问题。
然而，由于要投影到的集合不是一个子空间，我们不能简单地迭代地进行投影，我们必须使用投影的求解器（参见凸集交点的正交投影）。

在我看来，有3个选择：

投影梯度下降法 对目标函数进行梯度步骤，然后通过凸集交点上的正交投影方法来解决投影问题。

3项ADMM 将SPSD投影合并为一个单一函数。然后使用3项ADMM（其中一个投影需要内部迭代）。您可以使用PD3O或经典的3个运算符ADMM（参见三个运算符分裂方案及其优化应用）。特别是对于这种情况，可以参考凸二次半定规划和扩展的三块ADMM的三个运算符分裂视角。

4项ADMM 我还没有找到一篇论文来证明这种情况下的收敛性保证。但是值得一试。

我在Julia中实现了投影梯度下降法（1）和PD3O来解决这个问题。

参考解决方案是使用Convex.jl库。 在@WillemHekman的情况下，矩阵$ \boldsymbol{B} $是一个半正定矩阵。因此，迹$ \opertaorname{Tr}\left( \boldsymbol{A} \boldsymbol{B} \right) $保证是非负的（参见2个半正定矩阵相乘的非负性）。 这意味着我可以最小化目标函数的abs()，而不仅仅是实际值。这意味着它适用于复数矩阵。

该实现不依赖于此，并且可以解决任意方阵$ \boldsymbol{B} $的问题。

Julia代码可在我的StackOverflow Q35813091 GitHub存储库中找到（查看StackOverflow\Q35813091文件夹）。

备注：这个答案的动机是一个独立于通用凸优化求解器（如Convex.jl和JuMP.jl）的求解器。

- Royi