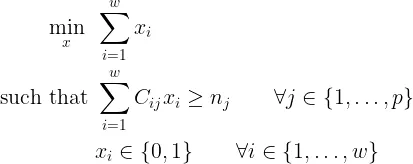第1部分(另见下面的第2部分)
您的任务看起来像是NP完全问题的
Set Cover Problem,因此解决时间呈指数级增长。
我决定(并在C++中实现)自己的解决方案,可能在一种情况下次指数级 - 如果许多仓库子集产生相同数量的产品。换句话说,如果所有仓库子集的指数大小(即2 ^ NumWarehouses)远大于所有仓库子集产生的所有产品计数的所有可能组合的集合。在像您这样的在线竞赛的大多数测试中,这种情况经常发生。如果发生这种情况,那么我的解决方案将在CPU和RAM方面都是亚指数级的。
我使用了
Dynamic Programming方法。整个算法可以描述如下:
我们创建一个映射,将每种产品的数量向量作为键,并指向一个三元组:a)前面取到当前产品数量的仓库集合,这是为了恢复精确选择的仓库;b)需要取的最小仓库数量;c)之前取到达此最小仓库数量的仓库。该集合初始化为单个键-0产品向量(0, 0,...,0)。
通过循环遍历所有仓库并执行3.-4.。
迭代映射中的所有当前产品数量(向量)并执行4。
对于迭代的产品向量(在映射中),我们添加迭代仓库的产品数量。这两个向量的总和是映射中的新键,在该键指向的值内,我们将索引添加到集合中,该集合表示已使用的仓库,同时将所需的最小仓库数量和之前使用的仓库设置为-1(未初始化)。
对于映射的每个键,使用递归函数找到所需的最小仓库数量,并找到实现此最小值的先前仓库。如果要给定键迭代Set中的所有仓库,并找到它们的最小值,则可以轻松地完成此操作,然后当前键的最小值将是所有最小值加1的最小值。
遍历映射中所有大于或等于(作为向量)订购产品数量的键。所有这些键都会给出解决方案,但只有其中一些会给出最小解决方案,保存给出所有最小解决方案的键。如果映射中的所有键都小于当前订购向量,则没有可能的解决方案,我们可以使用错误完成程序。
有了最小键,我们将所有已使用的仓库的路径恢复到达到此最小值。这很容易,因为对于映射中的每个键,我们保留最小仓库数量和应该取的先前仓库以实现此最小值。通过“上一个”仓库跳转,我们恢复所需仓库的整个路径。最后输出此找到的最小解决方案。
如上所述,该算法的内存和时间复杂度等于所有仓库子集中可以形成的不同向量乘积的数量。这可能是次指数级的(如果我们很幸运)或者不是次指数级的(如果我们不幸)。
下面是实现上述算法的完整C++代码(由我从头开始实现):
在线尝试!
#include <cstdint>
#include <vector>
#include <tuple>
#include <map>
#include <set>
#include <unordered_map>
#include <functional>
#include <stdexcept>
#include <iostream>
#include <algorithm>
#define ASSERT(cond) { if (!(cond)) throw std::runtime_error("Assertion (" #cond ") failed at line " + std::to_string(__LINE__) + "!"); }
#define LN { std::cout << "LN " << __LINE__ << std::endl; }
using u16 = uint16_t;
using u32 = uint32_t;
using u64 = uint64_t;
int main() {
std::vector<std::vector<u32>> warehouses_products = {
{2, 5, 0},
{1, 4, 4},
{3, 1, 4},
};
std::vector<u32> order_products = {5, 4, 1};
size_t const nwares = warehouses_products.size(),
nprods = warehouses_products.at(0).size();
ASSERT(order_products.size() == nprods);
std::map<std::vector<u32>, std::tuple<std::set<u16>, u16, u16>> d =
{{std::vector<u32>(nprods), {{}, 0, u16(-1)}}};
for (u16 iware = 0; iware < nwares; ++iware) {
auto const & wprods = warehouses_products[iware];
ASSERT(wprods.size() == nprods);
auto dc = d;
for (auto const & [k, _]: d) {
auto prods = k;
for (size_t i = 0; i < wprods.size(); ++i)
prods[i] += wprods[i];
dc.insert({prods, {{}, u16(-1), u16(-1)}});
std::get<0>(dc[prods]).insert(iware);
}
d = dc;
}
std::function<u16(std::vector<u32> const &)> FindMin =
[&](auto const & prods) {
auto & [a, b, c] = d.at(prods);
if (b != u16(-1))
return b;
u16 minv = u16(-1), minw = u16(-1);
for (auto iware: a) {
auto const & wprods = warehouses_products[iware];
auto cprods = prods;
for (size_t i = 0; i < wprods.size(); ++i)
cprods[i] -= wprods[i];
auto const fmin = FindMin(cprods) + 1;
if (fmin < minv) {
minv = fmin;
minw = iware;
}
}
ASSERT(minv != u16(-1) && minw != u16(-1));
b = minv;
c = minw;
return b;
};
for (auto const & [k, v]: d)
FindMin(k);
std::vector<u32> minp;
u16 minv = u16(-1);
for (auto const & [k, v]: d) {
bool matched = true;
for (size_t i = 0; i < nprods; ++i)
if (order_products[i] > k[i]) {
matched = false;
break;
}
if (!matched)
continue;
if (std::get<1>(v) < minv) {
minv = std::get<1>(v);
minp = k;
}
}
if (minp.empty()) {
std::cout << "Can't buy all products!" << std::endl;
return 0;
}
std::vector<u16> answer;
while (minp != std::vector<u32>(nprods)) {
auto const & [a, b, c] = d.at(minp);
answer.push_back(c);
auto const & wprods = warehouses_products[c];
for (size_t i = 0; i < wprods.size(); ++i)
minp[i] -= wprods[i];
}
std::sort(answer.begin(), answer.end());
std::cout << "WareHouses: ";
for (auto iware: answer)
std::cout << iware << ", ";
std::cout << std::endl;
}
Input:
WareHouses Products:
{2, 5, 0},
{1, 4, 4},
{3, 1, 4},
Ordered Products:
{5, 4, 1}
输出:
WareHouses: 0, 2,
第二部分:
我还实施了完全不同的解决方案。
现在它基于回溯,使用递归函数。
尽管这种解决方案在最坏情况下是指数级的,但经过一点时间后,它会给出接近最优解的解决方案。因此,您只需运行此程序,只要您能承担得起,无论它到目前为止找到了什么,都输出作为近似解决方案。
算法如下:
假设我们还需要购买一些产品。让我们按照尚未采取的所有仓库的所有产品总量的降序对其进行排序。
在循环中,我们从排序后的降序列表中取出每个下一个仓库,但我们只取此排序列表中的前limit(这是固定的给定值)个元素。通过这种方式,我们按照相关性的顺序贪婪地选择仓库,按照剩余待购买产品的数量的顺序。
在仓库被占用后,我们会递归进入当前函数,在其中再次形成一个排序的仓库列表,并取另一个最相关的仓库,换句话说跳转到此算法的1。
在每个函数调用时,如果我们购买了所有产品并且采取的仓库数量小于当前最小值,则输出此解决方案并更新最小值。
因此,上述算法从非常贪婪的行为开始,然后变得越来越慢,同时变得不那么贪婪,更像暴力方法。而且非常好的解决方案已经在第一秒钟出现。
例如,下面我创建了40个随机仓库,每个仓库有40个随机产品数量。这个相当大的任务在第一秒内可能以最优解得到解决。我的意思是,接下来的几分钟运行不会给出更好的解决方案。
在网上尝试!
#include <cstdint>
#include <iomanip>
#include <iostream>
#include <random>
#include <vector>
#include <functional>
#include <chrono>
#include <cmath>
using u8 = uint8_t;
using u16 = uint16_t;
using u32 = uint32_t;
using i32 = int32_t;
double Time() {
static auto const gtb = std::chrono::high_resolution_clock::now();
return std::chrono::duration_cast<std::chrono::duration<double>>(
std::chrono::high_resolution_clock::now() - gtb).count();
}
void Solve(auto const & wps, auto const & ops) {
size_t const nwares = wps.size(), nprods = ops.size(), max_depth = 1000;
std::vector<u32> prods_left = ops;
std::vector<std::vector<u16>> sorted_wares_all(max_depth);
std::vector<std::vector<u32>> prods_copy_all(max_depth);
std::vector<u16> path;
std::vector<u8> used(nwares);
size_t min_wares = size_t(-1);
auto ProdGrow = [&](auto const & prods){
size_t grow = 0;
for (size_t i = 0; i < nprods; ++i)
grow += std::min(prods_left[i], prods[i]);
return grow;
};
std::function<void(size_t, size_t, size_t)> Rec = [&](size_t depth, size_t off, size_t lim){
size_t prods_need = 0;
for (auto e: prods_left)
prods_need += e;
if (prods_need == 0) {
if (path.size() < min_wares) {
min_wares = path.size();
std::cout << std::endl << "Time " << std::setw(4) << std::llround(Time())
<< " sec, Cnt " << std::setw(3) << path.size() << ": ";
auto cpath = path;
std::sort(cpath.begin(), cpath.end());
for (auto e: cpath)
std::cout << e << ", ";
std::cout << std::endl << std::flush;
}
return;
}
auto & sorted_wares = sorted_wares_all.at(depth);
auto & prods_copy = prods_copy_all.at(depth);
sorted_wares.clear();
for (u16 i = off; i < nwares; ++i)
if (!used[i])
sorted_wares.push_back(i);
std::sort(sorted_wares.begin(), sorted_wares.end(),
[&](auto a, auto b){
return ProdGrow(wps[a]) > ProdGrow(wps[b]);
});
sorted_wares.resize(std::min(lim, sorted_wares.size()));
for (size_t i = 0; i < sorted_wares.size(); ++i) {
u16 const iware = sorted_wares[i];
auto const & wprods = wps[iware];
prods_copy = prods_left;
for (size_t j = 0; j < nprods; ++j)
prods_left[j] -= std::min(prods_left[j], wprods[j]);
path.push_back(iware);
used[iware] = 1;
Rec(depth + 1, iware + 1, lim);
used[iware] = 0;
path.pop_back();
prods_left = prods_copy;
}
for (auto e: sorted_wares)
used[e] = 0;
};
for (size_t lim = 1; lim <= nwares; ++lim) {
std::cout << "Limit " << lim << ", " << std::flush;
Rec(0, 0, lim);
}
}
int main() {
size_t const nwares = 40, nprods = 40;
std::mt19937_64 rng{std::random_device{}()};
std::vector<std::vector<u32>> wps(nwares);
for (size_t i = 0; i < nwares; ++i) {
wps[i].resize(nprods);
for (size_t j = 0; j < nprods; ++j)
wps[i][j] = rng() % 90 + 10;
}
std::vector<u32> ops;
for (size_t i = 0; i < nprods; ++i)
ops.push_back(rng() % (nwares * 20));
Solve(wps, ops);
}
输出:
Limit 1, Limit 2, Limit 3, Limit 4,
Time 0 sec, Cnt 13: 6, 8, 12, 13, 29, 31, 32, 33, 34, 36, 37, 38, 39,
Limit 5,
Time 0 sec, Cnt 12: 6, 8, 12, 13, 28, 29, 31, 32, 36, 37, 38, 39,
Limit 6, Limit 7,
Time 0 sec, Cnt 11: 6, 8, 12, 13, 19, 26, 31, 32, 33, 36, 39,
Limit 8, Limit 9, Limit 10, Limit 11, Limit 12, Limit 13, Limit 14, Limit 15,