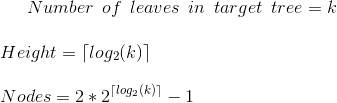如何确定线段树数组的所需大小?
线段树是一棵满二叉树。但我们要将其表示为一个数组。请注意,用数组表示高度为 h 的任何二叉树,需要的空间相当于高度为 h 的满二叉树。
[ Maximum possible Height of a Binary Tree with n nodes] (h) = Ceil[ Log_2 (n+1) ] - 1
[ No. of nodes in a Perfect Binary Tree of height h] (n) = 2 ^ (h+1) - 1
给定的数组表示线段树的叶子节点。因此,给定数组的大小将是叶子节点的数量。
在线段树中,每对叶子节点将由它们在上一级的父节点连接。这些父节点再次由它们在上一级的父节点连接。这样一直持续到根节点。
例子:
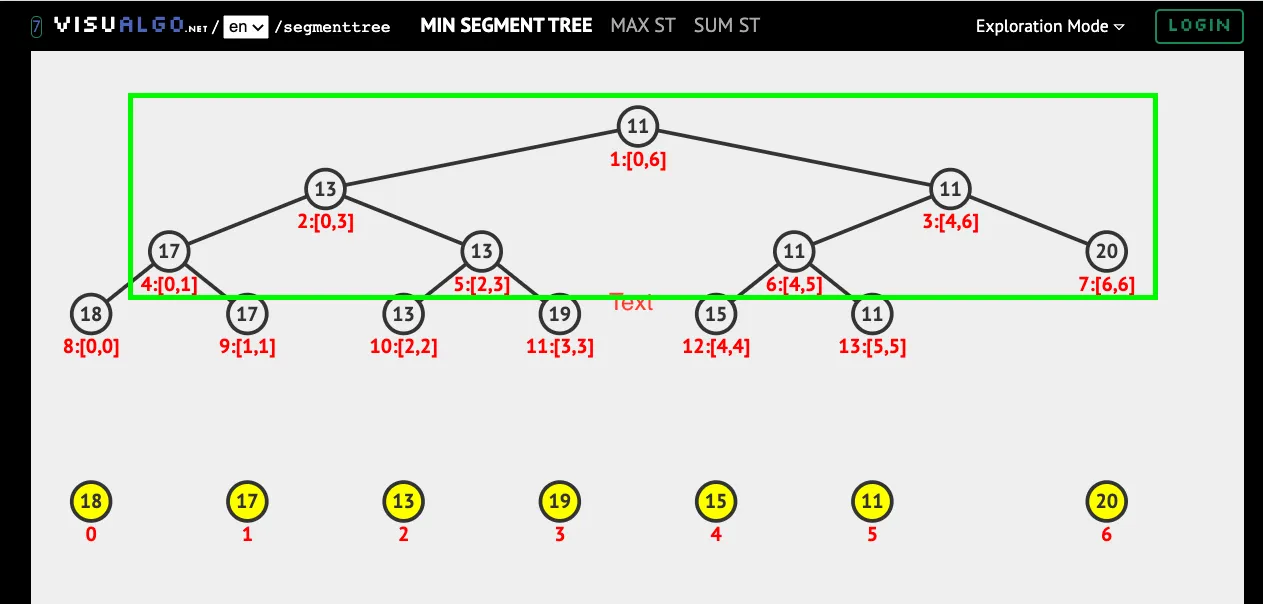
* Say, if there are 4 leaves in a Binary Tree, then the maximum no. of interior nodes in the Binary Tree will be N-1. So, 3.
- Then the total number of nodes in the Binary Tree = No. of interior nodes + No. of leaves. So, 4+3 = 7.
- The max possible height of this Binary Tree will be 2. Formula: Maximum possible Height of a Binary Tree (h) = Ceil[ Log_2 (n+1) ] - 1 .
- Remember, the total space required in the Segment Tree Array will be nothing but the total no. of nodes of the Perfect Binary Tree at this height.
- So, the total no. of nodes of the Perfect Binary Tree at this height is (n) = 7. Formula: No. of nodes in a Perfect Binary Tree (n) = 2 ^ (h+1) - 1.
- Thus the Segment Tree Array should also be of the size 7.
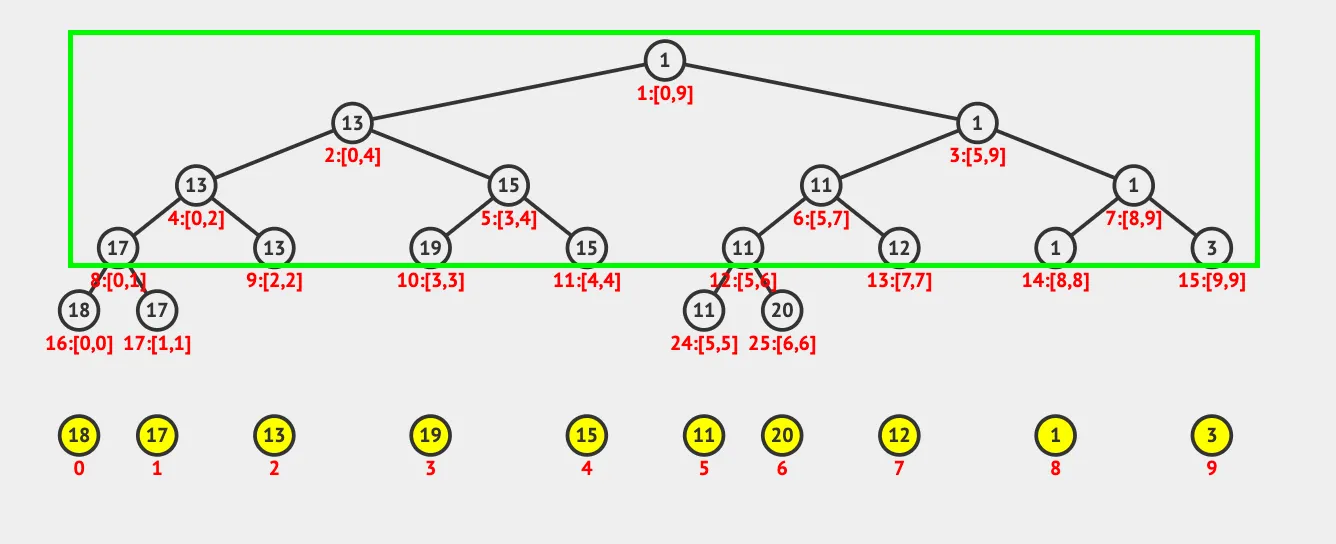
* But if there is one more leaf, say 5 and remember that this leaf can be anywhere between the beginning of the level till the end of the level.
- Then the total number of nodes in the Binary Tree = No. of interior nodes + No. of leaves. So, 5+4 = 9.
- The max possible height of this Binary Tree will be 3. Maximum possible Height of a Binary Tree (h) = Ceil[ Log_2 (n+1) ] - 1 .
- Remember, the total space required in the Segment Tree Array will be nothing but the total no. of nodes of the Perfect Binary Tree at this height.
- So, the total no. of nodes of the Perfect Binary Tree at this height is (n) = 15. Formula: No. of nodes in a Perfect Binary Tree (n) = 2 ^ (h+1) - 1.
- Thus the Segment Tree Array should also be of the size 15.
一般来说,
* Say, if there are N leaves in a Binary Tree, then the maximum no. of interior nodes in the Binary Tree will be N-1.
- Then the total number of nodes in the Binary Tree = No. of interior nodes + No. of leaves. So, 2N-1.
- The max possible height of this Binary Tree will be Ceil[ Log_2 (2N) ] - 1. Formula: Maximum possible Height of a Binary Tree (h) = Ceil[ Log_2 (n+1) ] - 1 .
- Remember, the total space required in the Segment Tree Array will be nothing but the total no. of nodes of the Perfect Binary Tree at this height.
- So, the total no. of nodes of the Perfect Binary Tree at this height is (n) = 2 ^ (Ceil[ Log_2 (2N) ] ) - 1. Formula: No. of nodes in a Perfect Binary Tree (n) = 2 ^ (h+1) - 1.
- Thus the Segment Tree Array should also be of the size 2 ^ (Ceil[ Log_2 (2N) ] ) - 1.
- This can also be written as [2*2 ^ (Ceil[ Log_2 (N) ] )] - 1.
因此,线段树数组的大小 = [2 * 2 ^ (Ceil[Log_2(N)])] - 1
线段树数组的大小简单地说就是4N(近似值)。
示例:
Best Case Scenario: (No. of leaves (N) is a power of 2)
Say, the no. of leaves , N is 4.
Since N is a power of 2, the Segment tree will be a Perfect Binary Tree.
So the total no of nodes will be N+N-1 = 2N-1 = 7
So, the size of the Segment Tree Array = 7.
Not the Best Case Scenario: (No. of leaves (N) is not a power of 2)
If the no. of leaves , N is 5.
Since N is not a power of 2, the Segment Tree will need one more entire level to accommodate the extra 1 leaf, as this leaf can be anywhere from the beginning of the level till the end.
We know that in a Perfect binary tree, the no of nodes in every new level, will be equal to No. of all the previous level nodes + 1.
Now, total no. of nodes in the segment tree upto the previous power of 2. i.e. 8 is 8+7 = 15
So, the no. of nodes in the new level will be 15+1 = 16
So, the size of the Segment Tree Array = 15 + 16 = 31.
总的来说,
Best Case Scenario: (No. of leaves (N) is a power of 2)
Since N is a power of 2, the Segment tree will be a Perfect Binary Tree.
So the total no of nodes will be N+N-1 = 2N-1
So, the size of the Segment Tree Array = 2N-1
Not the Best Case Scenario: (No. of leaves (N) is not a power of 2)
Since N is not a power of 2, the Segment Tree will need one more entire level to accommodate the extra leaves, as this leaf can be anywhere from the beginning of the level till the end.
We know that in a Perfect binary tree, the no of nodes in every new level, will be equal to No. of all the previous level nodes + 1.
Now, total no. of nodes in the segment tree upto the previous power of 2 will be 2N-1.
So, the no. of nodes in the new level will be 2N-1+1 = 2N
So, the size of the Segment Tree Array = 2N + 2N - 1 = 4N - 1 = 4N (approx.)
因此,线段树数组的大小约为4N。
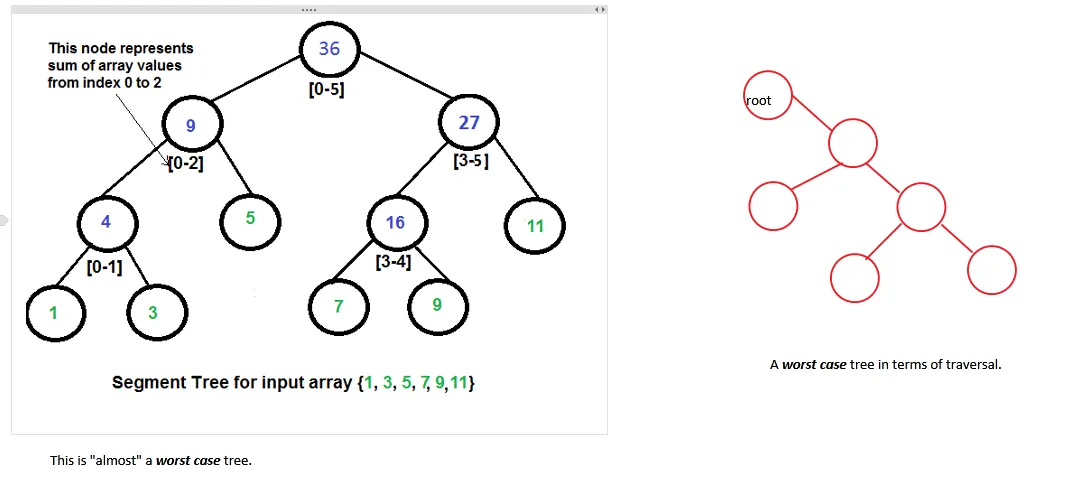 2. 我们的“最佳情况”。 这个树是完全平衡或完整的,将花费可预测的时间进行遍历。此外,这棵树也更好地被“hack”。
2. 我们的“最佳情况”。 这个树是完全平衡或完整的,将花费可预测的时间进行遍历。此外,这棵树也更好地被“hack”。