解决一个带依赖关系的简单打包组合问题

Question

这不是一道作业题，而是我正在处理的一个项目中遇到的问题。上图展示了一组盒子的装箱配置，其中A、B、C、D放在第一层，E、F、G放在第二层。问题是，如果将这些盒子随机排列，它们能否被放置在给定的配置中？

唯一的条件是所有盒子都必须从上往下放置，一旦放置就不能移动。因此，不能在已有的盒子下面滑动或悬浮放置，但可以为同一层的盒子节省空间。例如，只有当A和B已经放置好时，才能放置E。如果放置顺序是AEB...，那么它就无法放置在指定的配置中；如果放置顺序是ACBE...，那么E就可以正确地放置。

更具体的描述是，将装箱配置转换为一组依赖关系或前提条件。第一层的ABCD没有依赖关系，而E的依赖关系是{A和B}，F的依赖关系是{B和C}，G的依赖关系是{C和D}，相应的依赖关系必须在E或F或G发生之前发生。虽然这个问题不适用于此，但在某些问题中，依赖关系也可以是“或”关系而不是“与”关系。

我想知道解决这个问题的一般确定性算法，或者这类问题的算法？我能想到的一种方法是随机生成A、B、C、D、E、F、G的排列方式，重复进行10,000次，并在每个排列方式下检查每个元素调用时是否已经满足了相应的前提条件。然而，这个朴素的想法很耗时间，也不能产生精确的概率（我认为基于我实现的这个朴素算法，答案大约是1/18）。

非常感谢您的建议！

- Susie

---

你尝试过什么？ - touch my body

@user4343502 我在最后一段提到了我的当前想法。 - Susie

这是一个很酷的问题，但可能更适合 [math.se]。 - juanpa.arrivillaga

嗨@juanpa.arrivillaga，我同意这是个数学问题，不过我更想知道是否已经存在一种通用算法来解决这种问题。一旦问题扩大，数学上会变得非常混乱。 - Susie

Answer 1

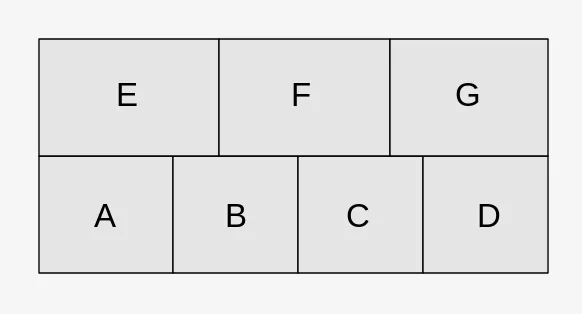
 E F G
A B C D

在您发布的这个具体示例中，有两种方式可以排列ABE和CDG，而且这两组可以以任何方式交织在一起。

4 * (3 + 4 - 1) choose 3 = 80

现在我们只需要在B和C之后放置F。分析F的索引分布，我们得到：

{2: 12, 3: 36, 4: 64, 5: 80, 6: 80}

尝试为这个特定的依赖关系制定一个公式，就像你所建议的那样，是“混乱”的。在这种情况下，我可能会先生成前两个金字塔的交错，然后计算在每个金字塔中放置 F 的方法数，因为组合解法似乎同样复杂。

要通常扩展这样的问题，可以通过对图形进行搜索并利用对称性来解决。在这种情况下，从 A 开始就类似于从 D 开始；B 与 C 相同。

Python 示例：

nodes = {
  'A': {
    'neighbours': ['B','C','D','E','F','G'], 'dependency': set()},
  'B': {
    'neighbours': ['A','C','D','E','F','G'], 'dependency': set()},
  'C': {
    'neighbours': ['A','B','D','E','F','G'], 'dependency': set()},
  'D': {
    'neighbours': ['A','B','C','E','F','G'], 'dependency': set()},
  'E': {
    'neighbours': ['C','D','F','G'], 'dependency': set(['A','B'])},
  'F': {
    'neighbours': ['A','D','E','G'], 'dependency': set(['B','C'])},
  'G': {
    'neighbours': ['A','B','E','F'], 'dependency': set(['C','D'])}
}

def f(key, visited):
  if len(visited) + 1 == len(nodes):
    return 1

  if nodes[key]['dependency'] and not nodes[key]['dependency'].issubset(visited):
    return 0

  result = 0

  for neighbour in nodes[key]['neighbours']:
    if neighbour not in visited:
      _visited = visited.copy()
      _visited.add(key)
      result += f(neighbour, _visited)

  return result

print 2 * f('A', set()) + 2 * f('B', set()) # 272

# Probability = 272 / 7! = 17 / 315 = 0.05396825396825397

- גלעד ברקן

---

这是一个深思熟虑的答案。我特别印象深刻的是你手算了概率...尽管已经比遍历所有排列要快得多，但是通用算法仍然可以进一步加速。例如，如果没有节点有依赖关系（例如，所有框都在同一层），则概率应为1，无需进行进一步计算，而使用此算法需要完全探索所有图形才能返回1。您是否有任何见解来进一步优化此算法，可能是通过根据它们的依赖关系预先分组节点？ - Susie

@Susie，关于如何进一步优化的问题很有趣。在我看来，每种情况可能都提供不同的优化线索，因此很难概括。直觉上，似乎依赖关系越复杂，遍历图形的速度就越快，概率也越低，这更有可能发生。 - גלעד ברקן

我从你的回答中得到了一些进一步优化问题的线索，即解决依赖图并将方块分成与其他方块存在无关的组。在这种特定情况下，这7个方块无法像那样被解决，但如果F不存在，则可以进行分组。根据您的经验，您能否建议一些快速的方法来将方块划分为这样的独立组？ - Susie

@Susie 很好的问题。也许可以发布一下以获得更多不同的反馈？ - גלעד ברקן

好的建议，我会这样做！ - Susie

我在 https://stackoverflow.com/questions/50126232/fastest-way-of-counting-all-possibilities-of-going-through-a-dependency-graph 上发布了一个新问题，之前从未参考过这个站点上的任何帖子，也无法正确地引用您的名字，请提供对新帖子的修改建议！谢谢。 - Susie

Answer 2

有5040（7！）种可能的排列。排列数量足够小，可以实现一个脚本来检查每个排列是否是“有效”排列（即：能够达到给定的配置）。您可以推断出概率：有效排列/所有排列

现在，问题变成了如何检查排列是否有效？如果我理解正确，仅当以下条件满足时，排列才有效：

• E在A和B之后
• F在B和C之后
• G在C和D之后

因此，代码变为（将A...B转换为0..6后）：

valids = 0
range7 = range(7)
for perm in itertools.permutations(range7):
    indexes = [perm.index(x) for x in range7]
    if (indexes[4] < indexes[0] or indexes[4] < indexes[1]):
        continue
    if (indexes[5] < indexes[1] or indexes[5] < indexes[2]):
        continue
    if (indexes[6] < indexes[2] or indexes[6] < indexes[3]):
        continue
    valids += 1
print(valids / 5040.)
# 5,39 %!

- ZZ ll

---

这是绝对正确且易于理解的，它比被接受的答案慢（对于这个特定情况慢了约30倍），但对于像这样的小问题来说并不太慢。 - Susie

Answer 3

这个问题可以通过计数方法解决。有两种类型的盒子：小盒子（S）和大盒子（L）。有N个不同的盒子排列方式，每个排列方式都与一个比特串相关联（例如：ABCDEFG是SSSSLLL或0000111）。

您可以找到数量上包括某个L字母在内的小盒子数量严格大于大盒子数量的排列数量。

例如，在SSLSSLL中，当您到达第一个L时，到该点为止有两个S和一个L（因此S>L），对于最后两个，S的数量大于L的数量。

- touch my body