在Haskell中广度优先构建一个二叉树（非二叉搜索树）

Question

我最近开始使用 Haskell，很可能只会用一小段时间。只是因为我在上大学的一个课程中被要求使用它来更好地理解函数式编程。

现在我遇到了一个小问题。我正在尝试按广度优先的方式构建它，但我觉得我的条件有些混乱，或者我的条件也可能是错误的。

因此，如果我输入 [“A1-Gate”, “North-Region”, “South-Region”, “Convention Center”, “Rectorate”, “Academic Building1”, “Academic Building2”] 和 [0.0, 0.5, 0.7, 0.3, 0.6, 1.2, 1.4, 1.2]，我的树应该像这样：

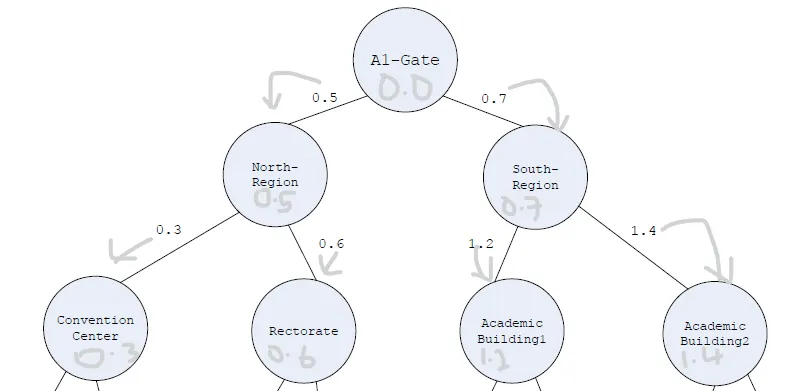
但我的测试结果并不是我预期的。所以一个有经验的 Haskell 专家可能会帮助我发现我做错了什么。

输出：

*Main> l1 = ["A1-Gate", "North-Region", "South-Region", "Convention Center", 
             "Rectorate", "Academic Building1", "Academic Building2"]
*Main> l3 = [0.0, 0.5, 0.7, 0.3, 0.6, 1.2, 1.4, 1.2]
*Main> parkingtree = createBinaryParkingTree l1 l3
*Main> parkingtree
Node "North-Region" 0.5 
   (Node "A1-Gate" 0.0 EmptyTree EmptyTree) 
   (Node "Convention Center" 0.3 
     (Node "South-Region" 0.7 EmptyTree EmptyTree) 
     (Node "Academic Building2" 1.4 
       (Node "Academic Building1" 1.2 EmptyTree EmptyTree) 
       (Node "Rectorate" 0.6 EmptyTree EmptyTree)))

A-1门应该是根，但它最终成为一个没有子级的子级，因此条件非常混乱。

如果我能得到一些指导，会很有帮助。以下是我目前写的内容：

data Tree = EmptyTree | Node [Char] Float Tree Tree deriving (Show,Eq,Ord)

insertElement location cost EmptyTree = 
   Node location cost EmptyTree EmptyTree
insertElement newlocation newcost (Node location cost left right) = 
   if (left == EmptyTree && right == EmptyTree)
   then Node location cost (insertElement newlocation newcost EmptyTree) 
                           right
   else if (left == EmptyTree && right /= EmptyTree)
        then Node location cost (insertElement newlocation newcost EmptyTree) 
                                right
        else if (left /= EmptyTree && right == EmptyTree)
             then Node location cost left 
                                (insertElement newlocation newcost EmptyTree)
             else Node newlocation newcost EmptyTree
                                (Node location cost left right)

buildBPT [] = EmptyTree
--buildBPT (xs:[]) = insertElement (fst xs) (snd xs) (buildBPT [])
buildBPT (x:xs) = insertElement (fst x) (snd x) (buildBPT xs)

createBinaryParkingTree a b = buildBPT (zip a b)

感谢提供任何可能的帮助。是的，我已经查看了一些类似的问题，但我认为我的问题是不同的，但如果您认为某篇文章有明确的答案可以帮助我，我愿意去看看。

- JDMukiibs

---

你说你的结果是错误的。请提供一个使用示例和它给出的不正确输出。 - amalloy

广度优先是在函数式或命令式语言中构建树的一种困难方向。通常，函数式树更容易自下而上地构建，创建一个父节点来合并其下面节点的结果。https://dev59.com/zU3Sa4cB1Zd3GeqPyM2n 看起来很相关。 - amalloy

@amalloy 哦，谢谢，我会查看那个问题的。当然，我会进行编辑以显示它带来的输出。 - JDMukiibs

@amalloy 我可以很容易地在Prolog中或任何具有可变结构的语言（如Scheme或C）中按BFS顺序构建树。它需要O(n)时间和O(n)辅助空间。在Prolog中，这本质上是一个一行代码：bfst(Xs,T):- bfst(Xs,[T|R],R). bfst(Xs,Ns,Z):- Xs=[] -> Z=[], maplist(=(empty),Ns) ; Xs=[X|Xs2], Ns=[node(X,L,R)|Ns2], Z=[L,R|Z2], bfst(Xs2,Ns2,Z2)。 - Will Ness

@WillNess，用Haskell高效地实现并不太难（请参见我的解决方案，基于amalloy的一般思路），但我还没有找到真正优美的方法。 - dfeuer

@dfeuer 再次感谢您的慷慨奖励，这很有趣，也很愉快。 :) - Will Ness

Answer 1

这是一个共递归的解决方案。

{-#  bft(Xs,T) :- bft( Xs, [T|Q], Q).    % if you don't read Prolog, see (*) 

     bft(     [],    Nodes ,      [])  :-  maplist( =(empty), Nodes).
     bft( [X|Xs], [N|Nodes], [L,R|Q])  :-  N = node(X,L,R), 
        bft( Xs,     Nodes,       Q).
#-}

data Tree a = Empty | Node a (Tree a) (Tree a) deriving Show

bft :: [a] -> Tree a
bft xs = head nodes    -- Breadth First Tree
  where
  nodes = zipWith g (map Just xs ++ repeat Nothing)  -- values and
                                                     --   Empty leaves...
                    (pairs $ tail nodes)             -- branches...
  g (Just x) (lt,rt)  =  Node x lt rt
  g Nothing  _        =  Empty
  pairs ~(a: ~(b:c))  =  (a,b) : pairs c
{-
  nodes!!0 = g (Just (xs!!0)) (nodes!!1, nodes!!2)            .
  nodes!!1 = g (Just (xs!!1)) (nodes!!3, nodes!!4)        .       .
  nodes!!2 = g (Just (xs!!2)) (nodes!!5, nodes!!6)      .   .   .   .
  ................                                    .................
-}

nodes 是结果树的所有子树的广度优先枚举。树本身是顶部子树，即此列表中的第一个。我们从输入 xs 中的每个 x 创建 Node，当输入用尽时，我们使用无限数量的 Nothing 创建 Empty（Empty 叶子节点的真实长度为 length xs + 1，但我们不需要关心这个）。

而且我们根本不需要计数。

测试：

> bft [1..4]
Node 1 (Node 2 (Node 4 Empty Empty) Empty) (Node 3 Empty Empty)

> bft [1..10]
Node 1 
   (Node 2 
      (Node 4 
         (Node 8  Empty Empty) 
         (Node 9  Empty Empty)) 
      (Node 5 
         (Node 10 Empty Empty) 
         Empty)) 
   (Node 3 
      (Node 6 Empty Empty) 
      (Node 7 Empty Empty))

---

它是如何工作的：关键在于g的懒惰，它不强制lt和rt的值，而元组结构则由非常懒惰的pairs提供。因此，当作为g的第二个和第三个参数提供时，两者都像Prolog伪代码(*)中的“尚未设置的变量”一样。但是，对于xs中的下一个x，被thislt引用的节点成为g结果的下一个调用。然后轮到rt等等。当xs结束并且我们遇到Nothing时，g停止从pairs的输出中提取值。因此，pairs也停止在nodes上前进，虽然它被定义为无尽的Empty流，但这只是为了安全起见而已。

---

(*) Prolog的变量是明确的set-once：它们被允许处于未分配状态。Haskell的(x:xs)就是Prolog的[X | Xs]。

伪代码：维护一个队列；将“未分配指针”入队；对于xs中的每个x：{将队列当前头部指针设为Node（x，lt，rt），其中lt，rt是未分配指针；将lt入队；将rt入队；弹出队列};将队列中剩余的所有指针设为Empty；在原始队列头部找到结果树，即原始第一个“未分配指针”（或者使用“空盒子”而不是“未分配指针”也是另一种选择）。

这个Prolog的“队列”当然是完全持久化的： “弹出”不会改变任何数据结构，也不会改变对队列前头的任何未完成引用——它只是将当前指针推进队列。因此，在所有这些排队之后，留下的是建立树节点的，树本身是其头元素——树是其顶部节点，两个子节点在枚举完成时完全实例化为底部叶子。

---

更新：@dfeuer提出了一个简化版版本，更接近Prolog原始版本（在帖子顶部的评论中），可以更加清晰。在他的帖子中查找更高效的代码和讨论等内容。对于子树队列，使用简单的[]而不是dfeuer使用的更有效的无限流类型data IS a = a :+ IS a，它变成了这样。

bftree :: [a] -> Tree a
bftree xs = t
    where
    t : q  =  go xs q
    go []       _              =  repeat Empty
    go (x:ys) ~(l : ~(r : q))  =  Node x l r : go ys q

      ---READ-- ----READ----      ---WRITE---

{-
   xs    =  [ x  x2  x3  x4  x5  x6  x7  x8   … ]
   (t:q) =  [ t  l   r   ll  lr  rl  rr  llr  …  Empty Empty  … … ]
-}

相比之下，树的广度优先枚举的相反操作是

bflist :: Tree a -> [a]
bflist t = [x | Node x _ _ <- q]
    where
    q  =  t : go 1 q
    go 0  _                =          []
    go i (Empty      : q)  =          go (i-1) q
    go i (Node _ l r : q)  =  l : r : go (i+1) q

         -----READ------     --WRITE--

如何使用 bftree： t : q 是树的子树列表，按广度优先顺序排列。特定的 go (x:ys) 调用在后续调用 go（使用另一个 x 在 ys 下面）或通过始终返回 Empty 的 go [] 来定义 l 和 r 之前使用。结果 t 是此列表中的第一个，即树的最顶层节点，即树本身。

这个树节点列表是通过递归调用 go 以与消耗输入值列表 xs 相同的速度创建的，但作为 go 的 输入 以 两倍 的速度消耗，因为每个节点有 两个 子节点。

这些额外的节点因此也必须定义为Empty叶子。我们不关心需要多少个，并且只需创建一个无限列表来满足任何需要，尽管空叶子的实际数量将比xs多一个。

实际上，这与计算机科学中几十年来用于基于数组的树的相同方案相同，其中树节点按广度优先顺序放置在线性数组中。有趣的是，在这种设置中，两种转换都是一个no-op——只有我们对相同数据的解释发生了变化，我们对它的处理方式，我们如何与/使用它进行交互。

- Will Ness

---

评论不适合进行长时间的讨论；此对话已被移至聊天室。 - Samuel Liew

Answer 2

更新：下面的解决方案是大O最优的，而且（我认为）相当易于理解，所以我将其留在这里，以防有人感兴趣。然而，Will Ness的解决方案更加美丽，尤其是在进行了一些优化之后，实际上可以期望表现更好。它更值得学习！

---

暂时忽略假边标签，只专注于核心内容。

算法设计中常见的一种模式是，有时候解决一个更普遍的问题可能会更容易。因此，我要看一下如何构建一个具有给定数量树的森林（树的列表），而不是试图构建一棵树。我会使节点标签多态化，以避免考虑它们的外观；当然，您也可以使用相同的构建技术来处理原始的树类型。

data Tree a = Empty | Node a (Tree a) (Tree a)

-- Built a tree from a breadth-first list
bft :: [a] -> Tree a
bft xs = case dff 1 xs of
  [] -> Empty
  [t] -> t
  _ -> error "something went wrong"

-- Build a forest of nonempty trees.
-- The given number indicates the (maximum)
-- number of trees to build.
bff :: Int -> [a] -> [Tree a]
bff _ [] = []
bff n xs = case splitAt n xs of
  (front, rear) -> combine front (bff (2 * n) rear)
  where
    combine :: [a] -> [Tree a] -> [Tree a]
    -- you write this

这是一个完整的、工业级、最大程度地懒惰的实现。这是我能够想出的最懒惰的有效版本。一个略微不那么懒惰的变体适用于完全定义的无限输入；我还没有尝试测试哪个在实践中更快。

bft' :: [a] -> Tree a
bft' xs = case bff 1 xs of
  [] -> Empty
  [t] -> t
  _ -> error "whoops"

bff' :: Int -> [a] -> [Tree a]
bff' !_ [] = []
bff' n xs = combine n xs (bff (2 * n) (drop n xs))
  where
    -- The "take" portion of the splitAt in the original
    -- bff is integrated into this version of combine. That
    -- lets us avoid allocating an intermediate list we don't
    -- really need.
    combine :: Int -> [a] -> [Tree a] -> [Tree a]
    combine 0 !_ ~[] = [] -- These two lazy patterns are just documentation
    combine _k [] ~[] = []
    combine k (y : ys) ts = Node y l r : combine (k - 1) ys dropped
      where
        (l, ~(r, dropped)) = case ts of  -- This lazy pattern matters.
          [] -> (Empty, (Empty, []))
          t1 : ts' -> (t1, case ts' of
            [] -> (Empty, [])
            t2 : ts'' -> (t2, ts''))

对于不那么懒惰的变体，请将(!l, ~(!r, dropped))替换为(!l, !r, dropped)并相应地调整右侧。

对于真正的工业强度，应使用严格按其元素排列的列表来表示森林：

data SL a = Cons !a (SL a) | Nil

在上述代码中，(l, ~(r, dropped)) 中的一对应该使用类似以下类型的表示方式：

```(l, Option<(r, bool)>)```

data LSP a b = LSP !a b

这样做可以避免一些（相当便宜的）运行时检查。更重要的是，这使得看出哪些地方被强制执行、哪些地方没有变得更容易。

- dfeuer

---

谢谢你的想法，我会尝试实现它。实际上，我也考虑过类似的东西，并使用 map 函数来映射我创建的树列表。你认为这也可能吗？如果是这样，你有什么提示可以帮助我将子节点映射到正确的父节点吗？ - JDMukiibs

@JDMukiibs，“map”在两个组合函数的情况下有点有用，但它并不是开始思考问题的正确位置。 - dfeuer

Prolog的变量是显式地设置为一次性的：它们允许处于未分配状态。Haskell的(x:xs)就是Prolog的[X | Xs]。----在伪代码中：维护一个队列；将“未分配指针”入队；对于xs中的每个x：{将队列当前头部的指针设置为Node(x, lt, rt)，其中lt、rt是未分配的指针；将lt和rt入队；弹出队列}; 将队列中剩余的所有指针设置为Empty；在原始队列的头部（即原始第一个“未分配指针”）中找到结果树。（或者用“空盒子”代替“未分配指针”也是另一种选择）。 - Will Ness

这个Prolog的“队列”当然是完全持久的： “弹出”不会改变任何数据结构，也不会改变对队列前头的任何未完成引用 - 它只是将当前指针推进队列。所以在所有这些排队的尾随中，留下的是建立树节点的bfs枚举，其中树本身是其头元素 - 树是其顶部节点，两个子节点在枚举完成时完全实例化为底部叶子。 - Will Ness

@dfeuer 我自己编写的 Prolog 代码阅读起来太过命令式了，:( 这就是阻碍我的原因。我回答中的 Haskell 代码实际上是它的近似翻译。 - Will Ness

Answer 3

你似乎选择的方法是从底部到顶部，从右到左地反向构建树；从列表的最后一个元素开始。这使得你的buildBPT函数看起来很好，但需要你的insertElement过于复杂。以这种方式广度优先构建二叉树需要在第三步之后的每一步都进行一些困难的中转。

添加8个节点到树中需要执行以下步骤（请注意节点是如何从最后一个插入到第一个的）：

   .              4                                                                                                                                                                                          
                6   6                                                                                                                                                                                        
   8           7 8 . .                                                                                                                                                                                       
  . .                                                                                                                                                                                                           
                  3                                                                                                                                                                                          
   7            4   5                                                                                                                                                                                        
  8 .          6 7 8 .                                                                                                                                                                                       

   6              2                                                                                                                                                                                          
  7 8           3   4                                                                                                                                                                                        
               5 6 7 8                                                                                                                                                                                       
   5                                                                                                                                                                                                         
 6   7            1                                                                                                                                                                                      
8 . . .       2       3                                                                                                                                                                                  
            4   5   6   7                                                                                                                                                                                
           8 . . . . . . .

如果你按从左到右，从上到下的顺序插入节点，则会得到一个更简单的解决方案，不需要旋转，而是需要一些树结构内省。请查看插入顺序；始终保持现有值的位置不变：

   .              1                                                                                                                                                                                               
                2   3                                                                                                                                                                                             
   1           4 5 . .                                                                                                                                                                                            
  . .                                                                                                                                                                                                             
                  1                                                                                                                                                                                               
   1            2   3                                                                                                                                                                                             
  2 .          4 5 6 .                                                                                                                                                                                            

   1              1                                                                                                                                                                                               
  2 3           2   3                                                                                                                                                                                             
               4 5 6 7                                                                                                                                                                                            
   1                                                                                                                                                                                                              
 2   3            1                                                                                                                                                                                           
4 . . .       2       3                                                                                                                                                                                       
            4   5   6   7                                                                                                                                                                                     
           8 . . . . . . .

插入步骤的渐进时间复杂度为O(n^2)，其中n是要插入的节点数，因为您正在逐个插入节点，然后迭代已经存在于树中的节点。

由于我们从左到右插入，技巧在于检查左子树是否完整：

• 如果它是完整的，并且右子树不完整，则递归到右边。
• 如果它是完整的，并且右子树也完整，则递归到左边（开始新行）。
• 如果它不是完整的，则递归到左侧。

以下是我的（更通用的）解决方案：

data Tree a = Leaf | Node a (Tree a) (Tree a)
            deriving (Eq, Show)

main = do
    let l1 = ["A1-Gate", "North-Region", "South-Region", "Convention Center", 
              "Rectorate", "Academic Building1", "Academic Building2"]
    let l2 = [0.0, 0.5, 0.7, 0.3, 0.6, 1.2, 1.4, 1.2]
    print $ treeFromList $ zip l1 l2

mkNode :: a -> Tree a
mkNode x = Node x Leaf Leaf

insertValue :: Tree a -> a -> Tree a
insertValue Leaf y = mkNode y
insertValue (Node x left right) y
    | isComplete left && nodeCount left /= nodeCount right = Node x left (insertValue right y)
    | otherwise = Node x (insertValue left y) right
    where nodeCount Leaf = 0
          nodeCount (Node _ left right) = 1 + nodeCount left + nodeCount right
          depth Leaf = 0
          depth (Node _ left right) = 1 + max (depth left) (depth right)
          isComplete n = nodeCount n == 2 ^ (depth n) - 1

treeFromList :: (Show a) => [a] -> Tree a
treeFromList = foldl insertValue Leaf

编辑：更详细的解释：

这个方法是为了记住插入节点的顺序：从左到右，然后从上到下。我在实际函数中压缩了不同情况，但你可以将它们扩展为三种情况：

1. 左侧已满吗？如果没有，则插入到左侧。
2. 右侧是否和已满的左侧一样完整？如果不是，则插入到右侧。
3. 两侧都已满，因此我们通过向左侧插入来开始一个新级别。

由于该函数从左到右逐步填充节点，并按照从上到下的顺序进行操作，因此我们始终知道（这是一个不变量）左侧必须在右侧之前填满，并且左侧深度不能超过右侧深度的1个级别（也不能比右侧浅）。

通过跟随第二组示例树的增长，您可以看到如何按照这个不变量插入值。这足以递归地描述该过程，因此它可以推广到任意大小的列表（递归是魔法）。

现在，我们如何确定一棵树是否“完整”？嗯，如果它完全平衡，或者在视觉上形成一个三角形，则它是完整的。因为我们正在处理二叉树，所以三角形的底部（填满时）必须具有等于2的幂的值的数量。更具体地说，它必须具有2^(depth-1)个值。在示例中进行计数：

• 深度=1->底部=1：2^(1-1)=1
• 深度=2->底部=2：2^(2-1)=2
• 深度=3->底部=4：2^(3-1)=4
• 深度=4->底部=8：2^(4-1)=8

底部以上的节点总数比底部的宽度少1：2^(n-1)-1。 因此，在完整树中的节点总数是在底部上方的节点数加上底部的节点数，因此：

num nodes in complete tree = 2^(depth-1) - 1 + 2^(depth-1)
                           = 2 × 2^(depth-1) - 1
                           = 2^depth - 1

现在我们可以说，如果一棵树恰好有2^depth - 1个非空节点，那么它是完整的。

因为我们从左到右、从上到下遍历，当左侧完成后，我们移动到右侧；当右侧“与左侧一样完整”（意味着它们具有相同数量的节点，这意味着根据不变量，它也是完整的）时，我们知道整棵树是完整的，因此必须添加一个新行。

最初我在这里有三个特殊情况：当两个节点都为空时，当左节点为空时（因此右节点也为空），以及当右节点为空时（因此左节点不可能为空）。这三种特殊情况被带有保护的最终情况所取代：

• 如果两侧都为空，则countNodes left == countNodes right，因此我们添加另一行（在左侧）。
• 如果左侧为空，则两侧都为空（见上一点）。
• 如果右侧为空，则左侧必须具有深度1和节点计数1，表示它是完整的，并且1 /= 0，因此我们向右侧添加。

- Billy Brown

---

哇，你刚刚真正点亮了我的脑海中的灯泡。我一直在为我所采取的路线所需的复杂性而苦苦挣扎。你能否更详细地启发我关于你的 insertValue 函数是如何实现的呢？ - JDMukiibs

我会在底部编辑我的答案，提供更详细的解释。 - Billy Brown

这看起来非常低效！ - dfeuer

你能看出如何完成我的解决方案，使其在O(n)时间内运行吗？ - dfeuer

@dfeuer 哦，我并不否认它的低效性（事实上，我在答案中提到了它是O(n^2)）。然而，我认为这是一个相当直观的解决方案；适合入门，但如果需要效率，则可以寻找一个O(n)的解决方案。 - Billy Brown