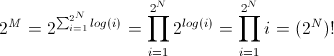这段代码列出一个集合的所有子集的时间复杂度是多少？

Question

这段代码列出一个集合的所有子集的时间复杂度是多少？

javabig-obit-manipulationtime-complexitypowerset

7

我在网上找到了很多O(2^n)复杂度的解决方案。有人能帮我算一下下面给出的代码的时间复杂度吗？此外，它涉及许多位操作，而我在这方面确实很弱，所以我没有完全掌握代码的要领。如果有人能解释一下这段代码就太好了。

private static void findSubsets(int array[])
{
  int numOfSubsets = 1 << array.length; 

  for(int i = 0; i < numOfSubsets; i++)
  {
    int pos = array.length - 1;
    int bitmask = i;

    System.out.print("{");
    while(bitmask > 0)
    {
      if((bitmask & 1) == 1)
         System.out.print(array[pos]+",");
     {
        bitmask >>= 1;
        pos--;
     }
     System.out.print("}");
  }
}

这是最优解吗？

- Abhiroop Sarkar

4个回答

8

这段代码的原理是利用了恰好具有n位二进制数字和n个元素集合子集之间的联系。如果将集合中的每个元素分配给一个单独的位，并将“1”视为“包括该元素在子集中”，将“0”视为“从子集中排除该元素”，那么您可以轻松地在两者之间进行转换。例如，如果集合包含a、b和c，则100可能对应于子集a，011可能对应于子集bc等。请尝试再次阅读此代码以获取这些见解。

就效率而言，上述代码在实践和理论上都非常快。列出子集的任何代码都必须花费大量时间来列出这些子集。所需的时间与必须列出的元素的总数成比例。此代码每项列出O(1)工作，因此在渐近意义下是最优的（当然，假设没有太多的元素使您溢出正在使用的整数）。

此代码的总复杂度可以通过计算打印的总元素数来确定。我们可以解决一些数学问题。请注意，大小为0的子集有n choose 0个，大小为1的子集有n choose 1个，大小为2的子集有n choose 2个，等等。因此，打印的总元素数由以下公式给出：

C = 0 × (n choose 0) + 1 × (n choose 1) + 2 × (n choose 2) + … + n × (n choose n)

请注意，（n选择k）=（n选择n-k）。因此：

C = 0 × (n choose n) + 1 × (n choose n - 1) + 2 × (n choose n - 2) + … + n × (n choose 0)

如果将这两个相加，我们得到：

2C = n × (n choose 0) + n × (n choose 1) + … + n × (n choose n) = n × (n choose 0 + n choose 1 + … + n choose n)

二项式定理表明括号内的表达式为2^n，因此：

2C = n2^n

所以

C = n2^(n-1)

因此，恰好打印了n2^(n-1)个元素，因此该方法的时间复杂度为Θ(n 2^n)。

希望对您有所帮助！

- templatetypedef

1

让我们假设array.length为n。此代码通过基于0到2^n的所有数字的二进制表示，选择或排除来自集合中的元素，这些数字正好是集合的所有组合。

由于numOfSubsets = 1 << array.length等于2^n，外部for循环的复杂度为O(2^n)。对于内部循环，您正在向右移动，最坏情况是111...1（n位设置为1），因此在最坏情况下，您将获得O(n)的复杂度。因此，总复杂度将为O(n*(2^n))。

- user987339

1

https://github.com/yaojingguo/subsets提供了两个算法来解决子集问题。 Iter算法与问题中给出的代码相同。 Recur算法使用递归访问每个可能的子集。两种算法的时间复杂度均为Θ(n*2^n)。在Iter算法中，1语句执行n*2^n次。 2语句执行n*2^(n-1)次（基于@templatetypedef的分析）。使用a表示1的成本。并使用b表示2的成本。总成本为n*2^n*a + n*2^(n-1)*b。

if ((i & (1 << j)) > 0) // 1
    list.add(A[j]); // 2

这里是Recur算法的主要逻辑：

result.add(new ArrayList<Integer>(list)); // 3
for (int i = pos; i < num.length; i++) { // 4
  list.add(num[i]);
  dfs(result, list, num, i + 1);
  list.remove(list.size() - 1);
}

语句 3 的代价与 1 相同，都是 n*2^(n-1)*b。其它的代价在循环 4 中。每次循环迭代包括三个函数调用。总共执行了 2^n 次循环。用 d 表示 4 的代价。总代价是 2^n*d + n*2^(n-1)*b。下面的图是集合 {1, 2, 3, 4} 对应的递归树。更精确的分析需要单独处理 2^(n-1) 个叶子节点。

Ø --- 1 --- 2 --- 3 --- 4 | | |- 4 | |- 3 --- 4 | |- 4 |- 2 --- 3 --- 4 | |- 4 |- 3 --- 4 |- 4

比较这两个算法的复杂度就是比较式子(1)的 n*2^n*a 和式子(2)的 2^n*d。将式子(1)除以式子(2)，得到 n * a / d。如果 n*a 小于 d，那么Iter比Recur更快。我使用Driver来测试这两个算法的效率。以下是一次运行的结果：

n: 16
Iter mills: 40
Recur mills: 19
n: 17
Iter mills: 78
Recur mills: 32
n: 18
Iter mills: 112
Recur mills: 10
n: 19
Iter mills: 156
Recur mills: 149
n: 20
Iter mills: 563
Recur mills: 164
n: 21
Iter mills: 2423
Recur mills: 1149
n: 22
Iter mills: 7402
Recur mills: 2211

这表明对于较小的n，Recur比Iter更快。

- Jingguo Yao

网页内容由stack overflow 提供, 点击上面的

可以查看英文原文，
原文链接

- bcorso · Accepted Answer

时间复杂度：

这里提供一种与@templatetypedef不同的推导时间复杂度的方式。

设代码中总步数为M。外层for循环运行2^N次，内层循环运行log(i)次，因此我们有：

enter image description here

将上述方程两边都乘以2并化简：

enter image description here

对上述方程两边取对数，并使用斯特林逼近公式(Log(x!) ~ xLog(x) - x)

enter image description here

位运算:

为了解决您在位运算方面的弱点，实际上不需要它。在您的代码中，它以三种方式使用，所有这些都可以用更少混淆的函数替换：

2的幂次方： (1 << array.length) → (Math.pow(2, array.length))
除以2： (x >>= 1) → (x /= 2)
取模2： (x & 1) → (x % 2)

代码解释:

此外，为了解释代码正在做什么，它基本上是使用这里所示的方法将每个数字（从0到2^N）转换为其二进制形式，正如@templatetypedef所说，1表示相应的元素在集合中。以下是使用此方法将156转换为二进制的示例：

enter image description here

作为带有您代码的示例：

pos = array.length - 1;
bitmask = 156;                              // as an example, take bitmask = 156
while(bitmask > 0){
    if(bitmask%2 == 1)                      // odd == remainder 1, it is in the set
         System.out.print(array[pos]+",");
    bitmask /= 2;                           // divide by 2
    pos--;
}

通过对所有位掩码（0到2^N）执行此操作，您可以找到所有唯一可能的集合。

编辑：

以下是比率的近似值（n2ⁿ/log₂(2ⁿ!)）的示例，可以看到随着n的增大，它很快接近于1：

enter image description here