背景
事实:
(m + n) C n = (m + n)! / (n! m!) = (1 / n!) * ((m + n)! / m!)
看代码:
第一行: den_prod=den_prod*each 表示 (1 / n!)
第二行: num_prod=num_prod*(hi+each) 表示简化形式的 ((m + n)! / m!)。
解决方案
关键思想是在for循环中使用模幂运算,然后对结果应用除模运算。除法运算变成了模数和模反元素的乘法。最后,为了计算模反元素,我们使用了欧拉定理。
def mod_inv (a, b):
return pow(a, b - 2, b)
mod_val=10**9+7
current=[int(x) for x in raw_input().strip().split()]
m=current[0]-1
n=current[1]-1
hi,lo=max(m,n),min(m,n)
num_prod=1
den_prod=1
for each in xrange(1,lo+1):
den_prod = (den_prod*each) % mod_val
num_prod = (num_prod*(hi+each)) % mod_val
print (num_prod * mod_inv(den_prod, mod_val)) % mod_val
性能
我对该问题进行了3种不同解决方案的计时。计时5000个组合:(5000 C n),其中n从0到4999。
代码1:上述解决方案
def mod_inv (a, b):
return pow(a, b - 2, b)
mod_val=10**9+7
hi = 5000
for lo in range(0, hi-1):
num_prod=1
den_prod=1
for each in xrange(1,lo+1):
den_prod = (den_prod*each) % mod_val
num_prod = (num_prod*(hi+each)) % mod_val
output = (num_prod * mod_inv(den_prod, mod_val)) % mod_val
时间 1:
real 0m3.607s
user 0m3.594s
sys 0m0.011s
代码2:您提出的解决方案
mod_val=10**9+7
hi = 5000
for lo in range(0, hi-1):
test1 = 1
test2 = 1
for each in xrange(1,lo+1):
test1 = (test1*each)
test2 = (test2*(hi+each))
test_output = (test2 / test1) % mod_val
时间 2:
real 0m25.377s
user 0m25.337s
sys 0m0.027s
代码3:
scipy解决方案
from scipy.misc import comb
hi = 5000
for lo in range(0, hi-1):
c = comb(hi+lo, lo, exact=True)
时间3:
real 0m36.700s
user 0m36.639s
sys 0m0.048s
大输入数据的API - 卢卡斯定理
def mod_inv (a, b):
return pow(a, b - 2, b)
def small_nCr (n, r, mod):
hi = max(r, (n - r))
lo = min(r, (n - r))
num_prod=1
den_prod=1
for each in range (1, lo + 1):
den_prod = (den_prod * each) % mod
num_prod = (num_prod * (hi + each)) % mod
small_c = (num_prod * mod_inv (den_prod, mod)) % mod
return small_c
def lucas (n, r, mod):
c = 1
while (n > 0 or r > 0):
ni = n % mod
ri = r % mod
if (ri > ni):
return 0
c = c * small_nCr (ni, ri, mod)
n = n / mod
r = r / mod
return c
def nCr (n, r, mod):
return lucas (n, r, mod) % mod
注意: 如果模数不是质数,您可以应用中国剩余定理。
来源:
模运算属性
模幂运算
模乘逆函数 - 使用pow函数的方法
Lucas定理
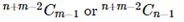
实际 0m3.645秒 用户 0m3.631秒 系统 0m0.011秒,基本相同。我会研究一下Lucas算法,感谢提醒!扩展欧几里得算法的代码在这里:https://en.wikibooks.org/wiki/Algorithm_Implementation/Mathematics/Extended_Euclidean_algorithm - The Brofessor