我们如何计算数组中每个元素右侧大于该元素的元素数量？

Question

我们如何计算数组中每个元素右侧大于该元素的元素数量？

c++arrayscalgorithmbig-o

20

给定一个包含n个元素的数组A，让数组X保存在索引i处的元素是原始数组A中右侧比A[i]大的元素数量。

例如，如果A为[10,12,8,17,3,24,19]，则X(A)为[4,3,3,2,2,0,0]。

如何以O(n log(n))时间复杂度和O(n)空间复杂度解决这个问题？

我可以使用循环轻松地以O(n^2)时间复杂度和O(1)空间复杂度解决此问题，对于每个元素，计算右侧有多少个元素比它大，但我没有满足要求。

我考虑使用快速排序，在最坏情况下可以在O(n log(n))的时间内完成，但我不知道排序后的数组如何帮助解决这个问题。

注意：关于快速排序，算法需要进行一些调整，以确保最坏情况下的时间复杂度为O(n log(n))，而不仅仅是平均情况。

- user15230795

4个回答

5

Telescope 在评论中首次提到可以使用二叉树来实现。然而，你也可以使用以下替代方法：

使用 AVL 树；
每个节点应存储元素及其右子树上的元素数量；
从数组末尾向开头迭代；
将元素添加到树中，并相应地更新节点上的大小。
在添加时，将当前元素与根进行比较；如果此元素小于根，则它小于右子树上的所有元素。在这种情况下，取该节点的大小，并继续到左子树并应用相同的逻辑。将最终大小添加到数组 X 上对应的位置；
如果它不小于根，则增加根的大小并继续到适当的子树。并应用前述逻辑。

时间复杂度将是 N 次插入到树中。因此，O(n log(n))。空间复杂度自然为 O(N)。

可视化：

A : [10,12,8,17,3,24,19];
X(A) [? ,? ,? ,? ,? ,? ,?]
右树节点大小 : S [?,?,?,?,?,?,?]

插入 19：

右子树中没有元素，因此：

19的大小=0；
X(A) [? ,? ,? ,? ,? ,? ,0]
S [?, ?, ?, ?, ?, ?, 0]

插入24：

24大于根节点（即19），因此让我们增加根节点的大小并进入右子树。
24的大小为0
X(A) [? ,? ,? ,? ,? ,0 ,0]
S [?, ?, ?, ?, ?, 0, 1]

插入3：

3小于根节点（即19），且根节点的大小为1，因此有2个元素大于3，即根节点和其右子树。我们向左走；
3的大小=0
X(A) [? ,? ,? ,? ,2 ,0 ,0]
S [? , ?, ?, ?, 0, 0, 1]

插入17：

17小于根节点（即19），且根节点的大小为1，因此有两个元素比17大，即根节点和其右子树。我们向左走，17比根节点（即3）大，让我们将节点3的大小从0增加到1，然后进入右子树。
17的大小=0
X(A) [? ,? ,? ,2 ,2 ,0 ,0]
S [? ,? ,? ,0 ,1 ,0 ,1]

插入8：

8比根节点小（即19），而根节点的大小为1，因此比8大的元素有2个，即根节点和它的右子树。我们向左走，8比根节点（即3）大，让我们将节点3的大小从1增加到2，然后进入右子树。8也比根节点（即17）小，所以到目前为止8比三个元素都要小。让我们向左走。
8的大小=0
X(A) [?, ?, 3, 2, 2, 0, 0]
S [?, ?, 0, 0, 2, 0, 1]

插入节点8时，进行了旋转以平衡树。

旋转期间，节点的大小也被更新，即节点8的大小从0变为1，节点3的大小从2变为0：- S [? ,? ,1 ,0 ,0 ,0 ,1]

插入12：

12小于根节点（即19），根节点的大小为1，因此大于12的元素有2个，即根节点和其右子树。我们往左走，12大于节点8，让我们将节点8的大小从1增加到2，并进入其右子树。12也小于17，目前有三个元素比12更大，让我们向左走。
节点12的大小=0
X(A) [? ,3 ,3 ,2 ,2 ,0 ,0]
S [? ,0 ,0 ,0 ,2 ,0 ,1]

通过插入节点12，执行双旋转来平衡树。

旋转期间，大小也会更新 - S [？，0，1，2，0，0，1]

插入10：

10小于根节点（即17），而根节点的大小为2，因此比10大的元素有3个，包括根节点和其右子树。我们向左移动，10大于根节点（即8），让我们将节点8的大小从1增加到2，并进入右子树。 10也小于根节点（即12），因此到目前为止，10小于4个元素。让我们向左移动。

10的大小= 0
X（A）[4,3,3,2,2,0,0]
S [0,0,0,0,2,0,1]

一个可能的C语言实现（AVL代码改编自源代码）：

#include<stdio.h>
#include<stdlib.h>
 
struct Node{
    int key;
    struct Node *left;
    struct Node *right;
    int height;
    int size;
};
 
int height(struct Node *N){
    return (N == NULL) ? 0 : N->height;
}

int sizeRightTree(struct Node *N){
    return (N == NULL || N -> right == NULL) ? 0 : N->right->height;
}
 
int max(int a, int b){
    return (a > b) ? a : b;
}
 
struct Node* newNode(int key){
    struct Node* node = (struct Node*) malloc(sizeof(struct Node));
    node->key   = key;
    node->left   = NULL;
    node->right  = NULL;
    node->height = 1;
    node->size = 0;
    return(node);
}
 
struct Node *rightRotate(struct Node *y) {
    struct Node *x = y->left;
    struct Node *T2 = x->right;
 
    x->right = y;
    y->left = T2;
 
    y->height = max(height(y->left), height(y->right))+1;
    x->height = max(height(x->left), height(x->right))+1;
    y->size = sizeRightTree(y);
    x->size = sizeRightTree(x);
    return x;
}
 
struct Node *leftRotate(struct Node *x){
    struct Node *y = x->right;
    struct Node *T2 = y->left;
 
    y->left = x;
    x->right = T2;
 
    x->height = max(height(x->left), height(x->right))+1;
    y->height = max(height(y->left), height(y->right))+1;
    y->size = sizeRightTree(y);
    x->size = sizeRightTree(x); 

    return y;
}
 
int getBalance(struct Node *N){
    return (N == NULL) ? 0 : height(N->left) - height(N->right);
}
 
struct Node* insert(struct Node* node, int key, int *size){
    if (node == NULL)
        return(newNode(key));
    if (key < node->key){
        *size = *size + node->size + 1;
        node->left  = insert(node->left, key, size);
    } 
    else if (key > node->key){
    node->size++;
    node->right = insert(node->right, key, size);
    }
    else 
        return node;
 
    node->height = 1 + max(height(node->left), height(node->right));
    int balance = getBalance(node);
 
    if (balance > 1 && key < node->left->key)
        return rightRotate(node);
    if (balance < -1 && key > node->right->key)
        return leftRotate(node);
    if (balance > 1 && key > node->left->key){
        node->left =  leftRotate(node->left);
        return rightRotate(node);
    }
    if (balance < -1 && key < node->right->key){
        node->right = rightRotate(node->right);
        return leftRotate(node);
    } 
    return node;
}

int main()
{
  int arraySize = 7;
  struct Node *root = NULL;
  int A[7] = {10,12,8,17,3,24,19};
  int X[7] ={0};
  for(int i = arraySize - 1; i >= 0; i--)
     root = insert(root, A[i], &X[i]);

  for(int i = 0; i < arraySize; i++)
     printf("%d ", X[i]);
  printf("\n");
  return 0;
}

输出：

4 3 3 2 2 0 0

- dreamcrash

0

类似于归并排序，但在处理范围的右侧和左侧之前插入计数，例如：

#include <algorithm>
#include <functional>

void count_greater_on_right( int* a, int* x, int begin, int end )
{
    if( end - begin <= 2 )
    {
        if( end - begin == 2 && a[begin] < a[begin+1] )
        {
            x[begin]+=1; // specific
            std::swap( a[begin], a[begin+1] );
        }
        return;
    }

    int middle =(begin+end+1)/2;
    count_greater_on_right( a, x, middle, end );

    // specific
    {
        for( int i=begin; i!=middle; ++i )
        {
            x[i]+=std::lower_bound( &a[middle], &a[end], a[i], std::greater<int>() )-&a[middle];
        }
    }

    count_greater_on_right( a, x, begin, middle );
    std::inplace_merge( &a[begin], &a[middle], &a[end], std::greater<int>() );
}

针对任务的代码使用// specific进行注释；反向排序使其稍微简单一些，个人认为；更新'a'，因此如果需要原始序列，请创建副本。

- Sergiy Kanilo

0

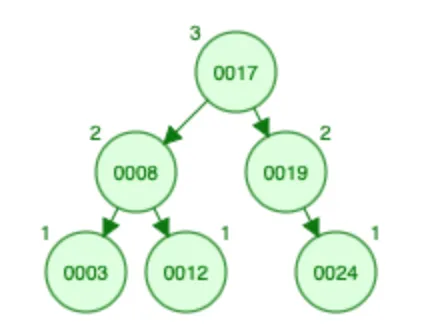
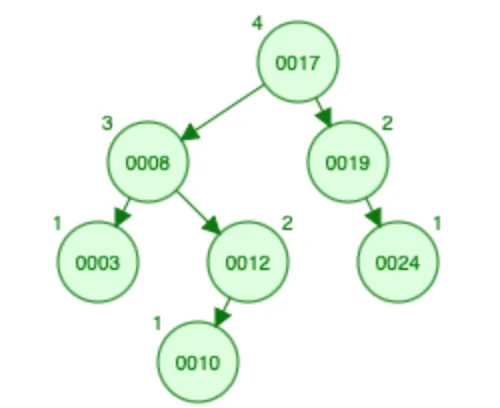
问题可以通过将数组分成子范围，然后对这些子范围进行排序来解决。让我们详细看一下，
给定数组 = [10, 12, 8, 17, 3, 24, 19]
现在将数组划分为长度为4的子范围，并按如下所示对这些子范围进行排序，
子范围排序数组

....................  ...............
| 8 | 10 | 12 | 17 |  | 3 | 19 | 24 |
....................  ...............
  2    0    1    3      4    6    5    => index

让我们来看一下子范围排序数组的第一个条目，即8，并尝试找到大于8的右侧元素数量。
正如您在上面看到的那样，8属于第一个子范围，因为子范围已经排序，子范围中的元素按升序排列，但不按其索引顺序排列。这意味着在当前子范围中，我们必须将所有右侧元素的索引与元素8的索引进行比较。

< p > 8 的索引是 2，但是 10 的索引是 0，这意味着 10 在输入数组中在 8 的左侧，
12 的索引也比 8 的索引小，这意味着 12 在输入数组中在 8 的左侧，
17 的索引是 3，大于 8 的索引，这意味着 17 在输入数组中在 8 的右侧，可以被视为更大的元素，
在比较当前子范围内所有右侧元素的索引与 8 的索引后，右侧更大的元素 count = 1，让我们看看下一个范围，

在子范围8之后，情况完全改变了，现在我们知道这个子范围位于元素8所属的子范围的右侧，这意味着我们不必将8的索引与此范围中的元素进行比较，所有元素都在元素8的右侧，我们只需要找到有多少个大于8的元素，

现在我们将右子范围的第一个元素与8进行比较，正如您在上面看到的，第一个元素是3，小于8，但是如果右子范围的第一个元素大于当前元素，则我们可以直接将计数器增加到右子范围中存在的元素数量。

因为第一个元素3小于8，所以我们在右侧子范围内找到8的上限，即19，而右侧子范围内的所有元素都大于8，因此有两个元素19，24，所以计数增加了2，变成了count=3
最终，比元素8大的右侧元素有3个。

通过类似的方式，可以找到所有元素的右侧大于的元素数量，结果数组将是,
x(A) = [4, 3, 3, 2, 2, 0, 0]

结论是，通过将输入数组分成排序的子范围，可以按以下步骤找到右侧的更大元素。

比较当前子范围内所有正确元素的索引，
比较右子范围的第一个元素，如果：
i. 第一个元素大于当前元素，则右侧范围的所有元素都大于当前元素，
ii. 第一个元素小于当前元素，则在右子范围中找到当前元素的上限，并且从右子范围中的上限开始的元素都大于当前元素。
对所有右子范围重复步骤2。

#include <iostream>

#include <vector>
#include <iterator>
#include <algorithm>

using std::cout;

std::vector<std::pair<int, std::size_t>> arrayOfSortedSubRange(std::size_t subRangeSize,
                                                              const std::vector<int>& numArr){


    std::vector<std::pair<int, std::size_t>> res;
    res.reserve(numArr.size());

    for(std::size_t i = 0, numArrSize = numArr.size(); i < numArrSize; ++i){

        res.emplace_back(numArr[i], i);
    }

    for(std::vector<std::pair<int, std::size_t>>::iterator it = res.begin(), endIt = res.end(); endIt != it;){

        std::vector<std::pair<int, std::size_t>>::iterator rangeEndIt = it + std::min<std::ptrdiff_t>(endIt - it,
                                                                                                      subRangeSize);

        std::sort(it, rangeEndIt, [](const std::pair<int, std::size_t>& a, const std::pair<int, std::size_t>& b){
            return a.first < b.first;});
        it = rangeEndIt;
    }

    return res;
}

std::size_t rightGreterElmentCountOfNumber(int num, std::vector<std::pair<int, std::size_t>>::const_iterator rightSubRangeIt,
                              std::vector<std::pair<int, std::size_t>>::const_iterator endIt){

    std::size_t count = 0;

    std::vector<std::pair<int, std::size_t>>::const_iterator subRangEndIt = rightSubRangeIt +
            std::min<std::ptrdiff_t>(endIt - rightSubRangeIt, 4);

    while(endIt != rightSubRangeIt){

        if(rightSubRangeIt->first > num){

            count += subRangEndIt - rightSubRangeIt;
        }
        else{
            count += subRangEndIt -
                    std::upper_bound(rightSubRangeIt, subRangEndIt, num, [](int num,
                                     const std::pair<int, std::size_t>& element){ return num < element.first;});
        }

        rightSubRangeIt = subRangEndIt;
        subRangEndIt += std::min<std::ptrdiff_t>(endIt - subRangEndIt, 4);
    }

    return count;
}

std::vector<std::size_t> rightGreaterElementCountForLessThanFiveNumbers(const std::vector<int>& numArr){

    std::vector<std::size_t> res(numArr.size(), 0);
    std::vector<std::size_t>::iterator resIt = res.begin();

    for(std::vector<int>::const_iterator it = numArr.cbegin(), lastIt = it + (numArr.size() - 1); lastIt != it;
        ++it, ++resIt){

        *resIt = std::count_if(it + 1, numArr.cend(), [num = *it](int rightNum){return rightNum > num;});
    }

    return res;
}

std::vector<std::size_t> rightGreaterElementCount(const std::vector<int>& numArr){

    if(numArr.size() < 5){

        return rightGreaterElementCountForLessThanFiveNumbers(numArr);
    }

    std::vector<std::size_t> resArr(numArr.size(), 0);
    std::vector<std::pair<int, std::size_t>> subRangeSortedArr = arrayOfSortedSubRange(4, numArr);

    for(std::vector<std::pair<int, std::size_t>>::const_iterator it = subRangeSortedArr.cbegin(),
        endIt = subRangeSortedArr.cend(); endIt != it;){

        std::vector<std::pair<int, std::size_t>>::const_iterator rightNextSubRangeIt = it + std::min<std::ptrdiff_t>(
                    endIt - it, 4);

        for(std::vector<std::pair<int, std::size_t>>::const_iterator eleIt = it; rightNextSubRangeIt != eleIt; ++eleIt){

            std::size_t count = std::count_if(eleIt, rightNextSubRangeIt, [index = eleIt->second](
                                              const std::pair<int, std::size_t>& element){ return index < element.second;});

            if(endIt != rightNextSubRangeIt){

                count += rightGreterElmentCountOfNumber(eleIt->first, rightNextSubRangeIt, endIt);
            }

            resArr[eleIt->second] = count;
        }

        it += std::min<std::ptrdiff_t>(endIt - it, 4);
    }

    return resArr;
}

int main(){

    std::vector<std::size_t> res = rightGreaterElementCount({10, 12, 8, 17, 3, 24, 19});

    cout<< "[10, 12, 8, 17, 3, 24, 19] => [";

    std::copy(res.cbegin(), res.cbegin() + (res.size() - 1), std::ostream_iterator<std::size_t>(cout, ", "));

    cout<< res.back()<< "]\n";
}

输出：
[10, 12, 8, 17, 3, 24, 19] => [4, 3, 3, 2, 2, 0, 0]

- Vikas Awadhiya

网页内容由stack overflow 提供, 点击上面的

可以查看英文原文，
原文链接

- Telescope · Accepted Answer

给定包含N个整数的数组A，构造一个数组X，使得对于每个i，X[i] = A中具有大于i索引且大于A[i]的元素数量。

可以使用二叉搜索树来解决此问题。从最后一个元素开始迭代，将每个元素添加到集合中，每次在元素e处时，使用二叉搜索树的find()操作查找当前树中大于e的元素数量。

也许您的第一个想法是使用std:: multiset（而不是std::set，因为我们可能会有重复的元素！），这是一棵自平衡二叉搜索树，提供O（logN）插入和O（logN）元素查找。这似乎适用于此算法，但实际上不是。原因是当调用std::multiset :: find（）时，它返回一个指向集合中元素的迭代器。查找集合中实际大于该元素的元素数量需要O（N）时间，因为要找到迭代器到集合末尾的距离需要反复递增它。

为了解决这个问题，我们使用了“索引多重集”，它是稍微修改过的二叉搜索树，以便我们可以在O（logN）时间内找到多重集合中元素的索引，同时仍支持O（logN）插入。以下是演示此数据结构的代码：

#include <iostream>
#include <vector>
#include <ext/pb_ds/assoc_container.hpp>

using namespace std;
using namespace __gnu_pbds;

// I know this is kind of messy, but it's the general way to get a C++ indexed
// multiset without using an external library
typedef tree <int, null_type, less_equal <int>, rb_tree_tag,
tree_order_statistics_node_update> indexed_set;

int main()
{
    int A_size;
    cin >> A_size;

    vector <int> A(A_size);
    for(int i = 0; i < A_size; ++i){
        cin >> A[i];
    }
    // Input Done

    indexed_set nums;
    vector <int> X(A_size);
    for(int i = A_size - 1; i >= 0; --i){
        // order_of_key returns the first index that A[i] would be at in a sorted list
        // with the same elements as nums.
        X[i] = nums.size() - nums.order_of_key(A[i]);

        nums.insert(A[i]);
    }

    for(int item : X){
        cout << item << " ";
    }
    cout << "\n";

    return 0;
}

因此，总的策略是：

从最后一个元素到第一个元素迭代。
对于每个元素，在 nums 中检查有多少个元素大于当前元素。 (O(logN))
然后，插入当前元素并继续迭代。 (O(logN)) 显然，这个算法的总时间复杂度是 O(NlogN)，空间复杂度是 O(N)。

对这种方法的观察和见解进行了快速总结：

见解：如果我们从最后一个元素到第一个元素迭代（而不是从第一个到最后一个），索引集仅包含给定迭代时当前元素右侧的元素，这正是我们想要的。这样做可以节约时间，因为我们不需要担心在从左到右迭代时将所有元素插入开头，然后逐个删除它们。
观察：这个算法中的二叉搜索树不能使用 std::set ，因为虽然它提供了在 O(logN) 时间内找到一个元素，但计算该元素在集合中的位置需要最坏情况下的 O(N) 时间。然而，索引集提供了这个“位置查找”操作和插入都是O(logN)的时间复杂度。