Networkx：获取有向无环图中所有可能的路径

Question

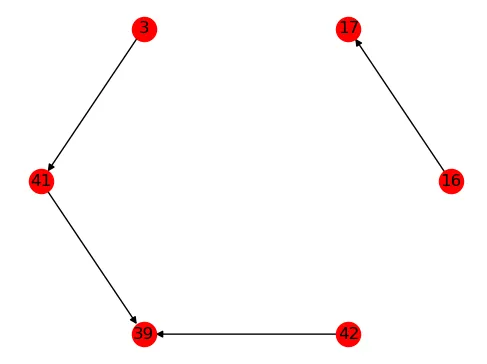
我正在尝试将一个有向（无环）图分割成方向连接的路径，依靠连通性：

当我测试弱连接和强连接子图时，我得到了以下结果：

Weak connectivity :
['16', '17'], ['3', '41', '39', '42']
Strong connectivity :
['17'], ['16'], ['39'], ['41'], ['3'], ['42']

我理解了弱连通性结果，但是对于强连通性结果并不理解，因为我期望得到3个子图：[16, 17]、[42, 39]和[3, 41, 39]。

我错过了什么？为什么只有单节点列表？如何获得预期结果？

下面是代码：

import networkx as nx
import matplotlib.pyplot as plt

G = nx.DiGraph()
G.add_edges_from([('16', '17'), ('3', '41'), ('41', '39'), ('42', '39')])

print("Weak connectivity : ")
for subgraph in (G.subgraph(c).copy() for c in nx.weakly_connected_components(G)) :
    print(subgraph.nodes)
print("Strong connectivity : ")
for subgraph in (G.subgraph(c).copy() for c in nx.strongly_connected_components(G)) :
    print(subgraph.nodes)

nx.draw_networkx(G, pos=nx.circular_layout(G))
plt.show()

- Arkeen

---

一个强连通分量被定义为一个子图，使得存在一条从任意节点到任意其他节点的路径。Networkx 给出的答案是正确的。也许你在寻找其他东西？ - DYZ

那么，[16, 17] 将成为一个强连通子图，因为你可以从 16 到达 17，对吧？或者你还需要能够从 17 到达 16 吗？ - Arkeen

“全向路径”这种说法并不存在。除非你正式定义它，否则无法计算。如果还有两条边(2,41)和(41,4)，预期输出会如何改变？ - DYZ

我现在意识到这与连接无关，我已经确定了一些过于具体的情况。一旦我知道自己真正需要什么，我会编辑我的帖子。 - Arkeen

当存在两条平行路径时（例如，1->2->3和1->2->4->5->3），请确保指定预期输出。路径的组合可能呈指数级增长。 - DYZ

Answer 1

因为评论和答案的帮助，我意识到“连接性”并不是我想要实现的一个正确的线索。明确一下：我想在有向无环图中获取所有起始节点到它们连接的终止节点之间的可能路径。

所以最终我自己编写了一个解决方案，这个方案相当容易理解，但可能不是最佳的，在性能或风格（pythonic/networkx）方面都有待改进。欢迎提出改进建议 :)

import networkx as nx
import matplotlib.pyplot as plt

G = nx.DiGraph()
G.add_edges_from([('16', '17'), ('3', '41'), ('41', '39'), ('42', '39')])

roots = []
leaves = []
for node in G.nodes :
  if G.in_degree(node) == 0 : # it's a root
    roots.append(node)
  elif G.out_degree(node) == 0 : # it's a leaf
    leaves.append(node)

for root in roots :
  for leaf in leaves :
    for path in nx.all_simple_paths(G, root, leaf) :
      print(path)

nx.draw_networkx(G, pos=nx.circular_layout(G))
plt.show()

（如果networkx中有内置函数，我显然错过了它）

- Arkeen

Answer 2

@Arkeen，你的解决方案看起来非常接近networkx文档中all_simple_paths的内容。它的描述如下：

    Iterate over each path from the root nodes to the leaf nodes in a
    directed acyclic graph passing all leaves together to avoid unnecessary
    compute::

        >>> G = nx.DiGraph([(0, 1), (2, 1), (1, 3), (1, 4)])
        >>> roots = (v for v, d in G.in_degree() if d == 0)
        >>> leaves = [v for v, d in G.out_degree() if d == 0]
        >>> all_paths = []
        >>> for root in roots:
        ...     paths = nx.all_simple_paths(G, root, leaves)
        ...     all_paths.extend(paths)
        >>> all_paths
        [[0, 1, 3], [0, 1, 4], [2, 1, 3], [2, 1, 4]]

我认为如果图中只有几个组件，则此方法可以很好地工作。但是，如果组件的数量很大，则此方法大部分时间都在尝试将根连接到其他组件中的叶子。但是，它仍然有效。

- brocla

Answer 3

你所缺少的是“强连通”的定义：强连通指的是有向图中，对于每一对顶点u和v，都存在从u到v和从v到u的路径。而强连通分量则是指最大的强连通子图。在你展示的图中，并不存在任何两个节点之间的强连通性，更不用说你列出的3个节点子图了。虽然你可以从3->41->39遍历，但是却没有回到41或者3的路径，因此该图并不是强连通的。

- Prune

Answer 4

根据强连通图的定义，您得到的结果是正确的。 定义：强连通图 如果有向图G=(V,E)中的每个顶点v都可以从V中的任何其他顶点到达，则称其为强连通图。

- sentence