多项式时间和指数时间
在分析算法时,以下是一些常见的大O函数。
- O(1) - 常数时间
- O(log(n)) - 对数时间
- O((log(n))c) - 多对数时间
- O(n) - 线性时间
- O(n log(n)) - 线性对数时间
- O(n2) - 平方时间
- O(nc) - 多项式时间
- O(cn) - 指数时间
- O(n!) - 阶乘时间
(n = 输入大小,c = 一些常数)
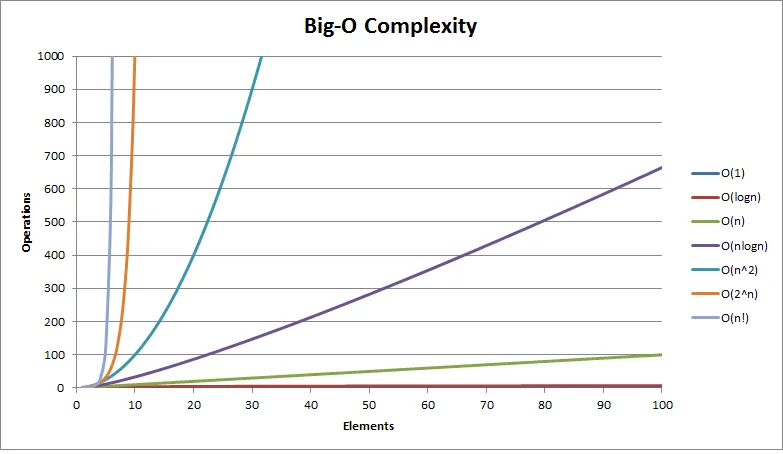
这是一个模型图,表示一些函数的大O复杂度。
5
看看这里。
指数级别的复杂度比多项式级别更糟糕。
O(n^2)属于二次型类别,它是多项式的一种(特殊情况下指数等于2),比指数级别更好。
指数级别的复杂度比多项式级别要糟糕得多。看看这些函数增长的方式。
n = 10 | 100 | 1000
n^2 = 100 | 10000 | 1000000
k^n = k^10 | k^100 | k^1000
当k小于类似于1.1这样的值时,k^1000就非常巨大了。例如,假设宇宙中的每个粒子每秒执行100亿亿亿次操作,那么需要数万亿年才能完成。
虽然我没有计算过具体数字,但是它确实非常大。
6
O(n^2)是多项式时间。该多项式为f(n)=n^2。另一方面,O(2^n)是指数时间,其中隐含的指数函数为f(n)=2^n。区别在于将n的函数放置在指数的底部还是指数本身。
任何指数增长函数都会比任何多项式函数更快地增长(从长期来看),因此这种区别对算法的效率特别是对于大值的n至关重要。
1
多项式时间。
多项式是一系列看起来像 常数 * x^k 的术语的总和。指数意味着类似于 常数 * k^x 的东西。
(在这两种情况下,k 是一个常数,x 是一个变量)。
指数算法的执行时间增长速度比多项式算法快得多。
指数函数 (如果至少有一个指数依赖于一个参数,则称其为指数函数):
- 例如 f(x) = 常数 ^ x
多项式函数 (如果没有指数依赖于某些函数参数,则称其为多项式函数):
- 例如 f(x) = x ^ 常数
2
指数函数的更精确定义
多项式 的定义非常普遍和直接,因此我不会进一步讨论它。
大O符号 的定义也相当普遍,你只需要仔细思考维基百科定义中的 M 和 x0,并通过一些例子来理解。
因此,在这个答案中,我想重点关注指数函数的精确定义,因为它需要更多的思考/不太为人所知/不太普遍,特别是当你开始思考一些边缘情况时。然后我将在下面进一步对比它与多项式。
- https://cstheory.stackexchange.com/questions/22588/is-it-right-to-call-2-sqrtn-exponential
- https://math.stackexchange.com/questions/55468/how-to-prove-that-exponential-grows-faster-than-polynomial
2^{polymonial(n)}
其中polynomial是一个多项式函数,需要满足以下条件:
- 不是常数函数,比如
1,否则时间复杂度也将会是常数级别。 - 最高次项系数为正,否则在无限趋近于无穷大时将会趋近于零,例如:
2^{-n^2 + 2n + 1}
因此,像这样的多项式函数将会是很好的选择:
2^{n^2 + 2n + 1}
请注意,基数2可以是大于1的任何数字,并且定义仍然有效,因为我们可以通过乘以指数来转换基数,例如:
8^{polymonial(n)} = (2^3)^{polymonial(n)} = 2^{3 * polymonial(n)}
并且3 * polymonial(n)也是一个多项式。
还要注意,常数的加法没有关系,例如2^{n+1}=2*2^{n},因此+1对于大O符号没有影响。
因此,对于任何小正数e,规范的“最小指数”的两个可能的好的大O等价选择是:
(1 + e)^{n}
2^{en}
对于非常小的e。
在这两种情况下,指数中多项式的最高阶项都是n ^ 1,一阶,因此是最小的非常数多项式。
这两个选择是等效的,因为我们可以将底数更改转换为指数乘数,如前面所述。
超多项式和次指数
但请注意,上述定义排除了在实践中出现且我们会倾向于称之为“指数”的一些仍然非常大的东西,例如:
2^{n^{1/2}}。 这有点像多项式,但它不是多项式,因为多项式幂必须是整数,在这里我们有1/22^{log_2(n)^2}
这些函数仍然非常大,因为它们的增长速度比任何多项式都要快。
但严格来说,它们的大O比我们对指数的严格定义要小!
这激发了以下定义:
- 超多项式:增长速度比任何多项式都快
- 次指数:增长速度比任何指数函数都慢,即
(1 + e)^{n}
本节中给出的所有示例都属于这两个类别。TODO 证明。
请记住,如果将某些东西放在指数上非常小,它可能会回到多项式,例如:
2^{log_2(n)} = n
对于小于log_2的任何内容,这也是正确的,例如:
2^{log_2(log_2(n))} = log_2(n)
是次多项式的。
重要的超多项式和次指数示例
the general number field sieve the fastest 2020-known algorithm for integer factorization, see also: What is the fastest integer factorization algorithm? That algorithm has complexity of the form:
e^{(k + o(1))(ln(n)^(1/3) * ln(ln(n)))^(2/3)}where
nis the factored number, and the little-o notationo(1)means a term that goes to 0 at infinity.That complexity even has a named generalization as it presumably occurs in other analyses: L-notation.
Note that the above expression itself is clearly polynomial in
n, because it is smaller thane^{ln(n)^(1/3) * ln(n))^(2/3)} = e^{ln(n)} = n.However, in the context of factorization, what really matters is note
n, but rather "the number of digits ofn", because cryptography parties can easily generate crypto keys that are twice as large. And the number of digits grows aslog_2. So in that complexity, what we really care about is something like:e^{(k + o(1))(n^(1/3) * ln(n)^(2/3)}which is of course both superpolynomial and sub-exponential.
The fantastic answer at: What would cause an algorithm to have O(log log n) complexity? gives an intuitive explanation of where the
O(log log n)comes from: whilelog ncomes from an algorithm that removes half of the options at each step, andlog log ncomes from an algorithm that reduces the options to the square root of the total at each step!https://quantumalgorithmzoo.org/ contains a list of algorithms which might be of interest to quantum computers, and in most cases, the quantum speedup relative to a classical computer is not strictly exponential, but rather superpolynomial. However, as this answer will have hopefully highlighted, this is still extremely significant and revolutionary. Understanding that repository is what originally motivated this answer :-)
It is also worth noting that we currently do not expect quantum computers to solve NP-complete problems, which are also generally expected to require exponential time to solve. But there is no proof otherwise either. See also: https://cs.stackexchange.com/questions/130470/can-quantum-computing-help-solve-np-complete-problems
https://math.stackexchange.com/questions/3975382/what-problems-are-known-to-be-require-superpolynomial-time-or-greater-to-solve询问了任何已被证明需要超多项式时间(且可能具有最优性证明,否则通用数筛将是一个显而易见的选择,但我们不知道它是否是最优的)的有趣算法。
证明指数函数在无穷大时始终大于多项式函数
讨论不同可能的次指数定义
多项式时间O(n)^k表示操作次数与输入规模的k次方成正比
指数时间O(k)^n表示操作次数与输入规模指数级成正比
多项式例子:n^2,n^3,n^100,5n^7等。
指数例子:2^n,3^n,100^n,5^(7n)等。
1
o(n平方)是多项式时间复杂度,而o(2^n)是指数时间复杂度。 如果p=np时是最佳情况,在最坏情况下p=np不相等,因为当输入大小n增长或输入大小增加时,它会变得更糟,并且处理的复杂度增长率会增加并且取决于n输入大小。当输入很小时,它是多项式的,当输入大小变得越来越大时,p=np不相等,这意味着增长率取决于输入的大小“N”。 优化、可满足性问题、团和独立集也在指数到多项式中遇到。
以下是针对新手的最简单解释:
多项式: 如果一个表达式包含或函数等于一个常数是一个变量的幂,例如
f(n) = 2 ^ n
while
指的是一个循环语句:
如果一个表达式包含或函数等于一个变量的常数幂 (如 e) 时,称之为指数函数。
f(n) = n ^ 2
2
原文链接
O(重写它)的O(n^n)- 举个例子 - 如果n = 3 ^ 360,那么n ^ n的十进制值约为10 ^ 174,大约有2 ^ 2 ^ 579个二进制位 - 这远远超出了GMP所能处理的范围,大约是::::::::::::::::::;2 ^ (2 ^ 30-1)左右。 - RARE Kpop Manifesto