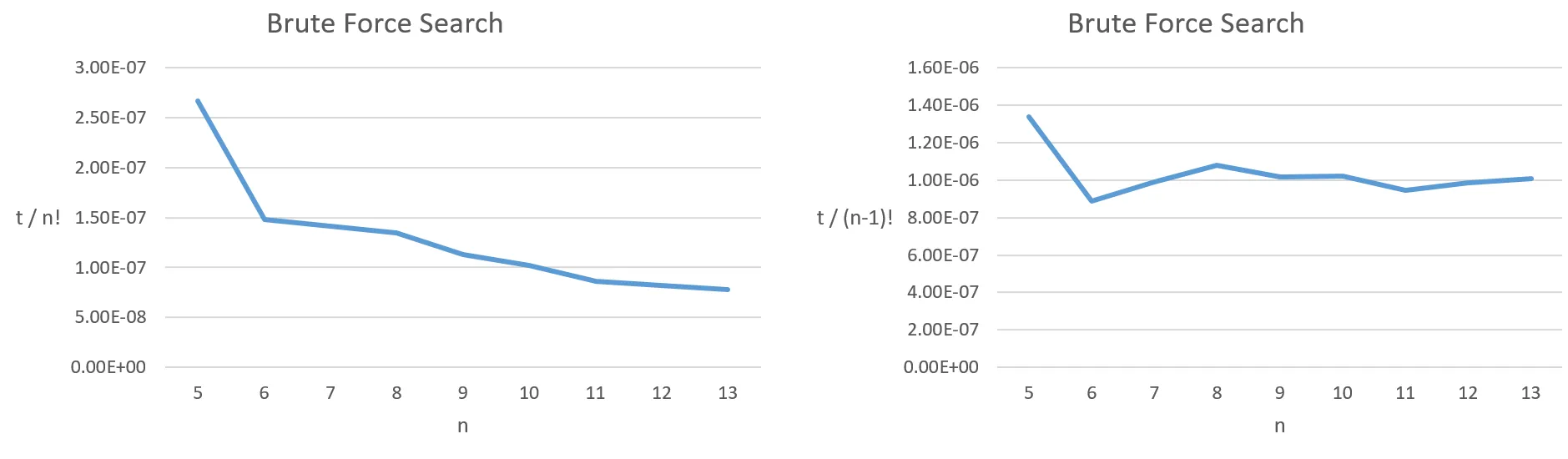
我的函数是O(n!)，还是O((n-1)!)更准确？

Question

我已经为旅行商问题编写了一个蛮力搜索算法，并测试了不同数量的“城市”所需的时间。从下面的图表中，我们可以看到时间大致与(n-1)!成正比，其中n是“城市”的数量。它不是直接与n!成正比的（毕竟，(n-1)! = n! / n）。

我的问题是，是否仍然正确地说该算法的运行时间为O(n!)，还是更好地说O((n-1)!)？我以前从未见过后者，但它似乎更准确。我在这里有些误解了。

[t = 花费时间, n = 城市数量]

- laurencevs

---

可能是Which Big-O grows faster asymptotically的重复问题。 - Idos

大O符号并不是用来实际计算算法的，而是提供一种抽象的比较方式。你的算法的最终行为是一个阶乘 - 它恰好是+1或-1并不重要。 - iAdjunct

Answer 1

根据定义，O(f(n))是所有被f(n)渐进占优的函数的集合，即所有函数g(n)，这些函数存在常数C和n_0，使得

g(n) < C * f(n)   for all n > n_0

由此定义可知，O(n!)实际上是O((n-1)!)的超集，因为函数f(n) = n!是第一个集合的成员，但不是第二个集合的成员。这两个集合实际上并不相同。

虽然如此，说你的问题是O(n!)是正确的，因为这只说明了一个上限。说你的问题是ϴ(n!)是不正确的，因为它表示了与常数因子相差无几的精确渐近行为。

实际上并没有太大的差别，正如另一个回答所指出的，你可以重新定义n，使其表示城市数量减一。

- Sven Marnach

---

这个答案使用了正确的方法。确实，通常情况下，如果 f 是一个多项式或指数函数，我们有 O(f(n)) = O(f(n-1))。然而，正如上面所指出的，对于所有函数来说这并不总是成立的：当 n -> infty 时，我们有 lim n!/(n-1)! = lim n = infty。 - chi

好的。我不会完全同意“在实践中没有太大的区别”这句话，对于增长速度像阶乘一样快的函数，我并不认同这种说法！换句话说，任何Θ(n!)算法只能用于非常小的输入；你永远没有机会将n变得足够大，以至于增加或减少一个数都是微不足道的。 - leftaroundabout

“你可以重新定义n表示城市数量减一。” 这是一个不好的想法，因为这会导致混淆。为什么不将其定义为sqrt（|cities|）呢？ - FooTheBar

Answer 2

O(n!)已经足够好了。对于大型的n来说，n或者n-1没有区别。

请看https://www.wikiwand.com/en/Time_complexity#/Table_of_common_time_complexities获取更多示例。

- Bartosz Bilicki

---

假设一个大数为n=100，那么O(n!)=9.33*10^157，而O((n-1)!)=9.33*10^155。你认为这两者没有区别吗？ :) - jbsu32

两个数都“大得惊人，无法用于大的n值”。因此，实际上并没有区别 :) 两个数字都比宇宙中估计的原子数量（仅为10^81）要大。 - Bartosz Bilicki

@jbsu32，那完全是胡说八道。O(...)是函数的一类，不能等于一个数字。而且，确实有O(10n) = O(n)，所以对于O符号来说，3990万和360万没有任何区别。 - user2512323

@jbsu32，“O（f（n））”是一个函数类，就像偶数函数或可微函数一样。这个类包括哪些内容由Sven（或者数学书籍）进行详细解释。如果我们将类视为属于该类的所有函数的集合（常见概念），那么是的，“O（10n）= O（n）= O（10 ^ 100n）”，因为它们的元素相同。 - user2512323

@jbsu32，O(10n)总是等于O(n)，因为我们不关心常数因子。 - Adam Stawicki

Answer 3

你可以简单地证明如下：

O((n-1)!) 意味着存在一个常数 c，使得算法步骤（或者时间复杂度）小于 c(n-1)! 小于 c n!/n 小于 c n! 对于每个 n>1。

因此，由于你的算法复杂度函数成立：

算法步骤（或者时间复杂度）

你的算法也是 O(n!)。

因此，我们证明了如果你的算法的时间复杂度为 O((n-1)!)，那么它也是 O(n!)。

- coder

Answer 4

Sven Marnach的回答非常好，我想稍微详细解释一下这部分：

“还是说我应该说O((n-1)!)？”

正如其他人所说，O(n)通常已经足够了。如果您确实想了解更多关于问题的信息，可以尝试找到并证明：

• 一个下限（通常用Ω(n)表示）
• 紧密的上限

下限基本上是说，在某些假设条件下，可能没有算法可以在渐近意义下更快地解决问题。紧密的上限是一个与下限相匹配的上限，即您必须证明Ω(f(n))的下限和O(f(n))的上限。如果您可以证明下限和紧密的上限，那么这意味着您的算法是该问题的渐近最优算法。

为了举一个具体的例子：您肯定知道像归并排序或快速排序这样的排序算法及其上限O(n log n)。Donald Knuth几十年前就证明，基于比较的整数排序算法至少需要n log n次比较，也就是说，需要Ω(n log n)次操作。由于我们有一个匹配的上限，因此归并排序和快速排序被认为是渐近最优的（尽管它们在实践中的性能差异很大）。

- mort