问题陈述
给定一组点 v₁, v₂, ..., vₙ，找到一个满足以下两个约束条件的大椭球体：
- 该椭球体在凸包 ℋ = ConvexHull(v₁, v₂, ..., vₙ) 中。
- 其中没有任何一个点 v₁, v₂, ..., vₙ 在该椭球体内部。
我提出了一种迭代过程来寻找符合这两个约束条件的大椭球体。在每次迭代中，我们需要解决一个半定规划问题。尽管这个迭代过程保证收敛，但它不能保证收敛到全局最大的椭球体。
方法
寻找单个椭球体
我们迭代过程的核心是在每次迭代中找到一个满足三个条件的椭球体：
- 该椭球体被包含在 ConvexHull(v₁, v₂, ..., vₙ) = {x | Ax<=b} 中。
- 对于一组点 u₁, ... uₘ（其中 {v₁, v₂, ..., vₙ} ⊂ {u₁, ... uₘ}，即点云中给定的点属于这组点 u₁, ... uₘ），该椭球体不包含任何点 u₁, ... uₘ。我们将这组点 u₁, ... uₘ 称为“外部点”。
- 对于一组点 w₁,..., wₖ（其中 {w₁,..., wₖ} ∩ {v₁, v₂, ..., vₙ} = ∅，即在 v₁, v₂, ..., vₙ 中没有任何一个点属于 {w₁,..., wₖ}），该椭球体包含所有点 w₁,..., wₖ。我们将这组点 w₁,..., wₖ 称为“内部点”。
直观的想法是，“内部点” w₁,..., wₖ 表示椭球体的体积。我们将添加新点到“内部点”中以增加椭球体的体积。
为了通过凸优化找到这样一个椭球体，我们将其参数化为
{x | xᵀPx + 2qᵀx ≤ r}
我们将搜索 P、q、r。
“外部点”u₁,...uₘ都在椭球体之外的条件可以表示为：
uᵢᵀPuᵢ + 2qᵀuᵢ >= r ∀ i=1, ..., m
这是对P、q、r的线性约束条件。
"内部点" w₁,..., wₖ 都在椭球内部的条件可以表述为：
wᵢᵀPwᵢ + 2qᵀwᵢ <= r ∀ i=1, ..., k
这也是对P、q、r的线性约束。
我们还会强制执行以下约束条件：
P is positive definite
当矩阵P是正定的，且存在点集wᵢ满足条件 wᵢᵀPwᵢ + 2qᵀwᵢ ≤ r 时，集合 {x | xᵀPx + 2qᵀx ≤ r} 就成为一个椭球体。
同时，我们还有一个约束条件，即椭球体在凸壳 ℋ（其中有l个半空间）内部（即 {x | aᵢᵀx≤ bᵢ, i=1,...,l} 的 H 表示）。利用 s-lemma，我们可以知道判断半空间 {x|aᵢᵀx≤ bᵢ} 是否包含该椭球体的必要和充分条件为：
∃ λᵢ >= 0,
s.t [P q -λᵢaᵢ/2] is positive semidefinite.
[(q-λᵢaᵢ/2)ᵀ λᵢbᵢ-r]
因此，我们可以解决以下半定规划问题，以找到包含所有“内部点”的椭球体，不包含任何“外部点”，并且在凸包 ℋ 内。
find P, q, r, λ
s.t uᵢᵀPuᵢ + 2qᵀuᵢ >= r ∀ i=1, ..., m
wᵢᵀPwᵢ + 2qᵀwᵢ <= r ∀ i=1, ..., k
P is positive definite.
λ >= 0,
[P q -λᵢaᵢ/2] is positive semidefinite.
[(q-λᵢaᵢ/2)ᵀ λᵢbᵢ-r]
我们将其称为P，q，r = find_ellipsoid（outside_points，inside_points，A，b）。
该椭球体积与（r + qᵀP⁻¹q）/ power（det（P），1 / 3）成比例。
迭代过程。
我们将“外部点”初始化为点云中的所有点v₁，v₂，...，vₙ，“内部点”则为凸包ℋ中的单个点w₁。在每次迭代中，我们使用上一子段中的find_ellipsoid函数查找包含所有“内部点”但不包含任何“外部点”的ℋ内椭球体。根据find_ellipsoid中SDP的结果，我们执行以下操作：
- 如果SDP可行，则比较新发现的椭球体和到目前为止发现的最大椭球体。如果此新椭球体更大，则将其接受为到目前为止发现的最大椭球体。
- 如果SDP不可行，则删除“内部点”中的最后一个点，并将此点添加到“外部点”。
在两种情况下，我们会在凸包ℋ中取一个新的样本点，将该样本点添加到“内部点”，然后再次解决SDP。
完整算法如下：
- 将“外部点”初始化为v₁，v₂，...，vₙ，将“内部点”初始化为凸包ℋ中的一个随机点。
- 当iter < max_iterations时：
- 解决SDP
P，q，r = find_ellipsoid（outside_points，inside_points，A，b）。
- 如果SDP可行且volume（Ellipsoid（P，q，r））> largest_volume，则设置
P_best = P，q_best = q，r_best = r。
- 如果SDP不可行，则pt = inside_points.pop_last（），outside_points.push_back（pt）。
- 在ℋ中随机抽取一个新点，将该点附加到“内部点”，iter += 1。进入步骤3。
代码
from scipy.spatial import ConvexHull, Delaunay
import scipy
import cvxpy as cp
import matplotlib.pyplot as plt
import numpy as np
from scipy.stats import dirichlet
from mpl_toolkits.mplot3d import Axes3D
def get_hull(pts):
dim = pts.shape[1]
hull = ConvexHull(pts)
A = hull.equations[:, 0:dim]
b = hull.equations[:, dim]
return A, -b, hull
def compute_ellipsoid_volume(P, q, r):
"""
The volume of the ellipsoid xᵀPx + 2qᵀx ≤ r is proportional to
power(r + qᵀP⁻¹q, dim/2)/sqrt(det(P))
We return this number.
"""
dim = P.shape[0]
return np.power(r + q @ np.linalg.solve(P, q)), dim/2) / \
np.sqrt(np.linalg.det(P))
def uniform_sample_from_convex_hull(deln, dim, n):
"""
Uniformly sample n points in the convex hull Ax<=b
This is copied from
https://dev59.com/l7fna4cB1Zd3GeqPysMd
@param deln Delaunay of the convex hull.
"""
vols = np.abs(np.linalg.det(deln[:, :dim, :] - deln[:, dim:, :]))\
/ np.math.factorial(dim)
sample = np.random.choice(len(vols), size=n, p=vols / vols.sum())
return np.einsum('ijk, ij -> ik', deln[sample],
dirichlet.rvs([1]*(dim + 1), size=n))
def centered_sample_from_convex_hull(pts):
"""
Sample a random point z that is in the convex hull of the points
v₁, ..., vₙ. z = (w₁v₁ + ... + wₙvₙ) / (w₁ + ... + wₙ) where wᵢ are all
uniformly sampled from [0, 1]. Notice that by central limit theorem, the
distribution of this sample is centered around the convex hull center, and
also with small variance when the number of points are large.
"""
num_pts = pts.shape[0]
pts_weights = np.random.uniform(0, 1, num_pts)
z = (pts_weights @ pts) / np.sum(pts_weights)
return z
def find_ellipsoid(outside_pts, inside_pts, A, b):
"""
For a given sets of points v₁, ..., vₙ, find the ellipsoid satisfying
three constraints:
1. The ellipsoid is within the convex hull of these points.
2. The ellipsoid doesn't contain any of the points.
3. The ellipsoid contains all the points in @p inside_pts
This ellipsoid is parameterized as {x | xᵀPx + 2qᵀx ≤ r }.
We find this ellipsoid by solving a semidefinite programming problem.
@param outside_pts outside_pts[i, :] is the i'th point vᵢ. The point vᵢ
must be outside of the ellipsoid.
@param inside_pts inside_pts[i, :] is the i'th point that must be inside
the ellipsoid.
@param A, b The convex hull of v₁, ..., vₙ is Ax<=b
@return (P, q, r, λ) P, q, r are the parameterization of this ellipsoid. λ
is the slack variable used in constraining the ellipsoid inside the convex
hull Ax <= b. If the problem is infeasible, then returns
None, None, None, None
"""
assert(isinstance(outside_pts, np.ndarray))
(num_outside_pts, dim) = outside_pts.shape
assert(isinstance(inside_pts, np.ndarray))
assert(inside_pts.shape[1] == dim)
num_inside_pts = inside_pts.shape[0]
constraints = []
P = cp.Variable((dim, dim), symmetric=True)
q = cp.Variable(dim)
r = cp.Variable()
for i in range(num_outside_pts):
constraints.append(
outside_pts[i, :] @ (P @ outside_pts[i, :]) +
2 * q @ outside_pts[i, :] >= r)
epsilon = 1e-6
constraints.append(P - epsilon * np.eye(dim) >> 0)
for i in range(num_inside_pts):
constraints.append(
inside_pts[i, :] @ (P @ inside_pts[i, :]) +
2 * q @ inside_pts[i, :] <= r)
num_faces = A.shape[0]
lambda_var = cp.Variable(num_faces)
constraints.append(lambda_var >= 0)
Q = [None] * num_faces
for i in range(num_faces):
Q[i] = cp.Variable((dim+1, dim+1), PSD=True)
constraints.append(Q[i][:dim, :dim] == P)
constraints.append(Q[i][:dim, dim] == q - lambda_var[i] * A[i, :]/2)
constraints.append(Q[i][-1, -1] == lambda_var[i] * b[i] - r)
prob = cp.Problem(cp.Minimize(0), constraints)
try:
prob.solve(verbose=False)
except cp.error.SolverError:
return None, None, None, None
if prob.status == 'optimal':
P_val = P.value
q_val = q.value
r_val = r.value
lambda_val = lambda_var.value
return P_val, q_val, r_val, lambda_val
else:
return None, None, None, None
def draw_ellipsoid(P, q, r, outside_pts, inside_pts):
"""
Draw an ellipsoid defined as {x | xᵀPx + 2qᵀx ≤ r }
This ellipsoid is equivalent to
|Lx + L⁻¹q| ≤ √(r + qᵀP⁻¹q)
where L is the symmetric matrix satisfying L * L = P
"""
fig = plt.figure()
dim = P.shape[0]
L = scipy.linalg.sqrtm(P)
radius = np.sqrt(r + q@(np.linalg.solve(P, q)))
if dim == 2:
theta = np.linspace(0, 2 * np.pi, 200)
sphere_pts = np.vstack((np.cos(theta), np.sin(theta)))
ellipsoid_pts = np.linalg.solve(
L, radius * sphere_pts - (np.linalg.solve(L, q)).reshape((2, -1)))
ax = fig.add_subplot(111)
ax.plot(ellipsoid_pts[0, :], ellipsoid_pts[1, :], c='blue')
ax.scatter(outside_pts[:, 0], outside_pts[:, 1], c='red')
ax.scatter(inside_pts[:, 0], inside_pts[:, 1], s=20, c='green')
ax.axis('equal')
plt.show()
if dim == 3:
u = np.linspace(0, np.pi, 30)
v = np.linspace(0, 2*np.pi, 30)
sphere_pts_x = np.outer(np.sin(u), np.sin(v))
sphere_pts_y = np.outer(np.sin(u), np.cos(v))
sphere_pts_z = np.outer(np.cos(u), np.ones_like(v))
sphere_pts = np.vstack((
sphere_pts_x.reshape((1, -1)), sphere_pts_y.reshape((1, -1)),
sphere_pts_z.reshape((1, -1))))
ellipsoid_pts = np.linalg.solve(
L, radius * sphere_pts - (np.linalg.solve(L, q)).reshape((3, -1)))
ax = plt.axes(projection='3d')
ellipsoid_pts_x = ellipsoid_pts[0, :].reshape(sphere_pts_x.shape)
ellipsoid_pts_y = ellipsoid_pts[1, :].reshape(sphere_pts_y.shape)
ellipsoid_pts_z = ellipsoid_pts[2, :].reshape(sphere_pts_z.shape)
ax.plot_wireframe(ellipsoid_pts_x, ellipsoid_pts_y, ellipsoid_pts_z)
ax.scatter(outside_pts[:, 0], outside_pts[:, 1], outside_pts[:, 2],
c='red')
ax.scatter(inside_pts[:, 0], inside_pts[:, 1], inside_pts[:, 2], s=20,
c='green')
ax.axis('equal')
plt.show()
def find_large_ellipsoid(pts, max_iterations):
"""
We find a large ellipsoid within the convex hull of @p pts but not
containing any point in @p pts.
The algorithm proceeds iteratively
1. Start with outside_pts = pts, inside_pts = z where z is a random point
in the convex hull of @p outside_pts.
2. while num_iter < max_iterations
3. Solve an SDP to find an ellipsoid that is within the convex hull of
@p pts, not containing any outside_pts, but contains all inside_pts.
4. If the SDP in the previous step is infeasible, then remove z from
inside_pts, and append it to the outside_pts.
5. Randomly sample a point in the convex hull of @p pts, if this point is
outside of the current ellipsoid, then append it to inside_pts.
6. num_iter += 1
When the iterations limit is reached, we report the ellipsoid with the
maximal volume.
@param pts pts[i, :] is the i'th points that has to be outside of the
ellipsoid.
@param max_iterations The iterations limit.
@return (P, q, r) The largest ellipsoid is parameterized as
{x | xᵀPx + 2qᵀx ≤ r }
"""
dim = pts.shape[1]
A, b, hull = get_hull(pts)
hull_vertices = pts[hull.vertices]
deln = hull_vertices[Delaunay(hull_vertices).simplices]
outside_pts = pts
z = centered_sample_from_convex_hull(pts)
inside_pts = z.reshape((1, -1))
num_iter = 0
max_ellipsoid_volume = -np.inf
while num_iter < max_iterations:
(P, q, r, lambda_val) = find_ellipsoid(outside_pts, inside_pts, A, b)
if P is not None:
volume = compute_ellipsoid_volume(P, q, r)
if volume > max_ellipsoid_volume:
max_ellipsoid_volume = volume
P_best = P
q_best = q
r_best = r
else:
inside_pts = inside_pts[:-1, :]
else:
outside_pts = np.vstack((outside_pts, inside_pts[-1, :]))
inside_pts = inside_pts[:-1, :]
sample_pts = uniform_sample_from_convex_hull(deln, dim, 20)
is_in_ellipsoid = np.sum(sample_pts.T*(P_best @ sample_pts.T), axis=0)\
+ 2 * sample_pts @ q_best <= r_best
if np.all(is_in_ellipsoid):
return P_best, q_best, r_best
else:
inside_pts = np.vstack((
inside_pts, sample_pts[np.where(~is_in_ellipsoid)[0][0], :]))
num_iter += 1
return P_best, q_best, r_best
if __name__ == "__main__":
pts = np.array([[0., 0.], [0., 1.], [1., 1.], [1., 0.], [0.2, 0.4]])
max_iterations = 10
P, q, r = find_large_ellipsoid(pts, max_iterations)
我也将代码放在github仓库中。
结果
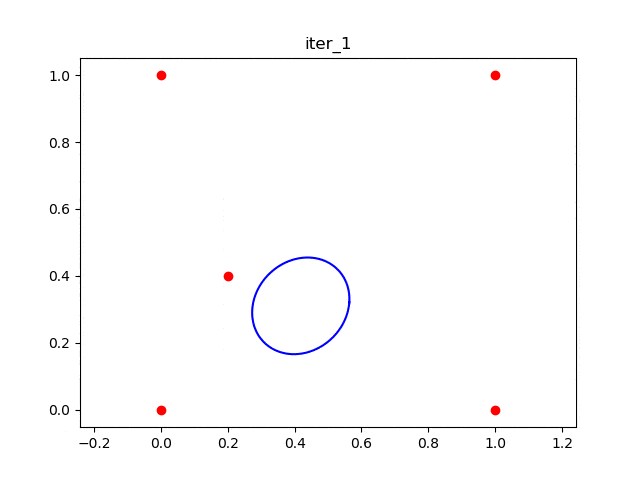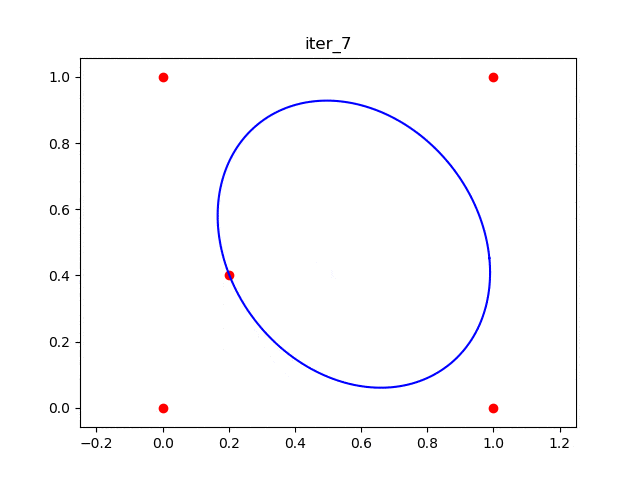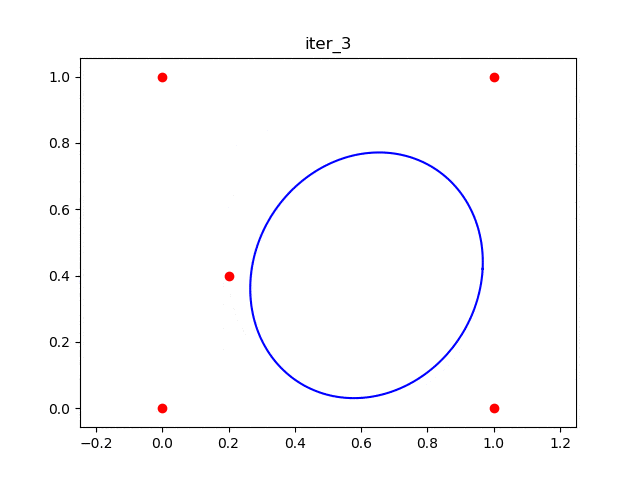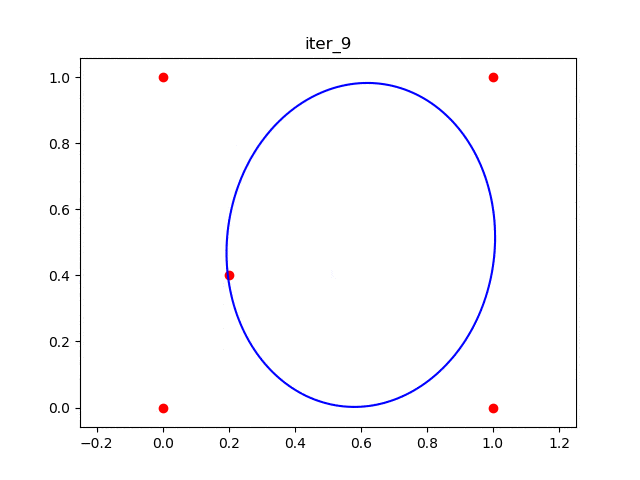
这是一个简单的二维例子，假设我们想要找到一个大的椭球体，它不包含下图中的五个红点。 这是第一次迭代后的结果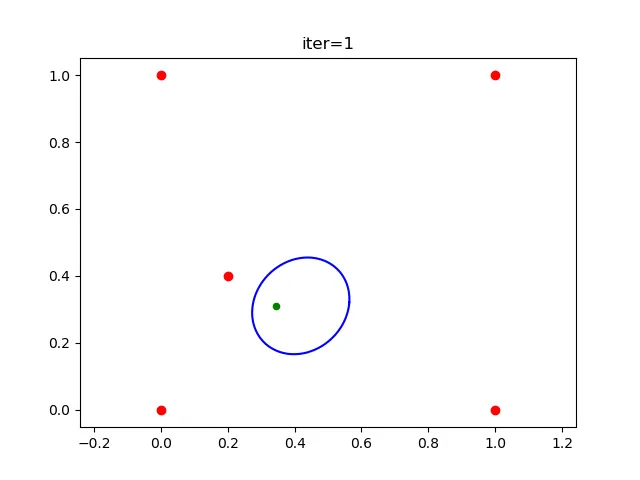
。 红色的点是“外部点”（初始的外部点是v₁，v₂，...，vₙ），绿色的点是初始的“内部点”。
在第二次迭代中，椭球体变成了
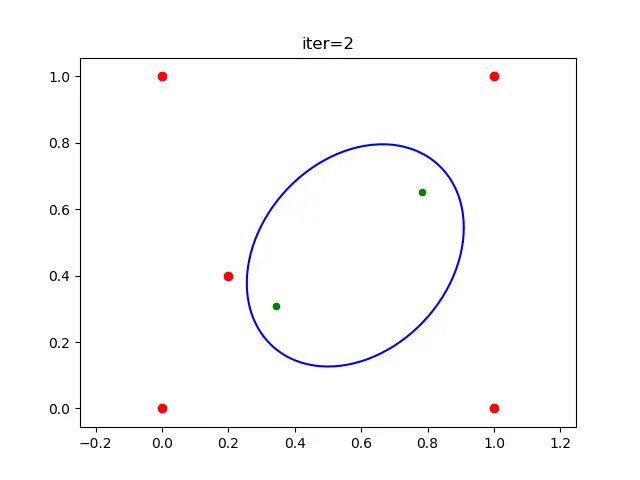。 通过添加一个“内部点”（绿色圆点），椭球体变得更大。
这个gif展示了10次迭代的动画。
