通过QR分解、SVD（和Cholesky分解？）计算投影/帽子矩阵。

Question

我正在尝试在R中计算一个任意的 N x J 矩阵 S 的投影矩阵 P：

P = S (S'S) ^ -1 S'

我一直在尝试使用以下函数执行此操作：

P <- function(S){
  output <- S %*% solve(t(S) %*% S) %*% t(S)
  return(output)
}

但是当我使用它时，会出现以下类似的错误:

# Error in solve.default(t(S) %*% S, t(S), tol = 1e-07) : 
#  system is computationally singular: reciprocal condition number = 2.26005e-28

我认为这是数值下溢和/或不稳定性的结果，正如r-help和此处所讨论的那样。但我对使用SVD或QR分解修复问题或将现有代码投入实践不够熟练。我还尝试了建议的代码，即将solve编写为系统：

output <- S %*% solve (t(S) %*% S, t(S), tol=1e-7)

但是它仍然无法正常工作。如有建议，将不胜感激。

我相当确定我的矩阵应该是可逆的，并且没有任何共线性，只是因为我尝试使用正交虚拟变量矩阵进行测试，但它仍然无法正常工作。

此外，我想将其应用于相当大的矩阵，因此我正在寻找一个简洁的通用解决方案。

- bikeclub

---

你不想使用 princomp 或 prcomp 有什么原因吗？计算主成分不需要手动完成。 - Paul Hiemstra

很抱歉，没有通用的解决方案，如果这是条件数，那么你就有问题了。 - Dr G

嗨，我并不是想做PCA，而是想实现一个我读过的估计器。我觉得很奇怪，即使对于一个简单的虚拟仪器矩阵，我也无法让它工作，因为这似乎保证不共线。 - bikeclub

1. 为什么不发布你的S矩阵？还有S'S？
2. 使用“典型”的S矩阵怎么样？
3. 尝试在t（S）％*％S周围加上括号？

- power

Answer 1

尽管 OP 已经超过一年没有活跃了，但我仍然决定发表一个回答。在统计学中，我们经常需要在线性回归背景下使用投影矩阵，因此我会使用 X 而不是 S。其中，X 是模型矩阵，y 是响应向量，而 H = X(X'X)^{-1}X' 是帽子 / 投影矩阵，因此 Hy 给出预测值。

这个答案假设普通最小二乘的情况。对于加权最小二乘，请参见从 QR 分解获取加权最小二乘回归的帽子矩阵。

---

概述

solve 基于一般方阵的 LU 分解。对于对称的 X'X（应该通过 crossprod(X) 计算，而不是在 R 中使用 t(X) %*% X，请参阅 ?crossprod 以了解更多信息），我们可以使用基于 Choleksy 分解的 chol2inv。

然而，三角分解比 QR 分解不太稳定。这不难理解。如果 X 的条件数为 kappa，那么 X'X 的条件数将为 kappa ^ 2。这可能会导致很大的数值困难。您收到的错误消息如下：

# system is computationally singular: reciprocal condition number = 2.26005e-28

这只是在说明：kappa ^ 2约为e-28，远小于机器精度约e-16。使用容差 tol = .Machine$double.eps，X'X将被视为秩不足，因此 LU 和 Cholesky 分解会崩溃。

通常情况下，我们会在这种情况下切换到 SVD 或 QR 方法，但带轴点的 Cholesky 分解是另一种选择。

• SVD 是最稳定的方法，但太昂贵了；
• QR 具有令人满意的稳定性，计算成本适中，并且在实践中常用；
• 带轴点的 Cholesky 快速，稳定性可接受。 对于大矩阵，它更受欢迎。

接下来，我将解释这三种方法。

---

使用 QR 分解

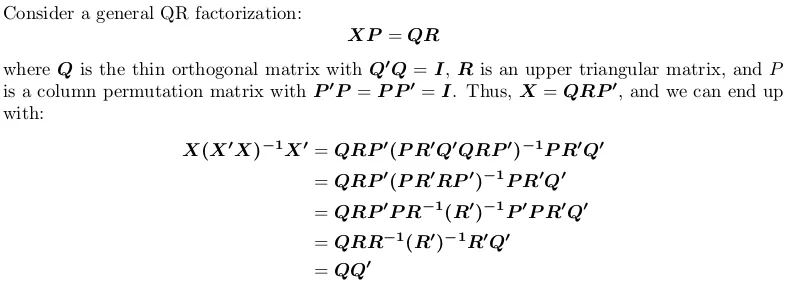
注意，投影矩阵与置换无关，即执行 QR 分解时是否使用轴点无关紧要。

在 R 中，qr.default 可以调用 LINPACK 例程 DQRDC 进行非轴点 QR 分解，并使用 LAPACK 例程 DGEQP3 进行块带轴点 QR 分解。 让我们生成一个玩具矩阵并测试两个选项：

set.seed(0); X <- matrix(rnorm(50), 10, 5)
qr_linpack <- qr.default(X)
qr_lapack <- qr.default(X, LAPACK = TRUE)

str(qr_linpack)
# List of 4
# $ qr   : num [1:10, 1:5] -3.79 -0.0861 0.3509 0.3357 0.1094 ...
# $ rank : int 5
# $ qraux: num [1:5] 1.33 1.37 1.03 1.01 1.15
# $ pivot: int [1:5] 1 2 3 4 5
# - attr(*, "class")= chr "qr"

str(qr_lapack)
# List of 4
# $ qr   : num [1:10, 1:5] -3.79 -0.0646 0.2632 0.2518 0.0821 ...
# $ rank : int 5
# $ qraux: num [1:5] 1.33 1.21 1.56 1.36 1.09
# $ pivot: int [1:5] 1 5 2 4 3
# - attr(*, "useLAPACK")= logi TRUE
# - attr(*, "class")= chr "qr"

注意两个对象的$pivot是不同的。

现在，我们定义一个包装函数来计算QQ'：

f <- function (QR) {
  ## thin Q-factor
  Q <- qr.qy(QR, diag(1, nrow = nrow(QR$qr), ncol = QR$rank))
  ## QQ'
  tcrossprod(Q)
  }

我们将看到，qr_linpack和qr_lapack会给出相同的投影矩阵：

H1 <- f(qr_linpack)
H2 <- f(qr_lapack)

mean(abs(H1 - H2))
# [1] 9.530571e-17

---

使用奇异值分解

在 R 中，svd 函数可以计算矩阵的奇异值分解。我们仍然使用上面的示例矩阵 X：

SVD <- svd(X)

str(SVD)
# List of 3
# $ d: num [1:5] 4.321 3.667 2.158 1.904 0.876
# $ u: num [1:10, 1:5] -0.4108 -0.0646 -0.2643 -0.1734 0.1007 ...
# $ v: num [1:5, 1:5] -0.766 0.164 0.176 0.383 -0.457 ...

H3 <- tcrossprod(SVD$u)

mean(abs(H1 - H3))
# [1] 1.311668e-16

我们再次得到相同的投影矩阵。

---

使用枢轴Cholesky分解

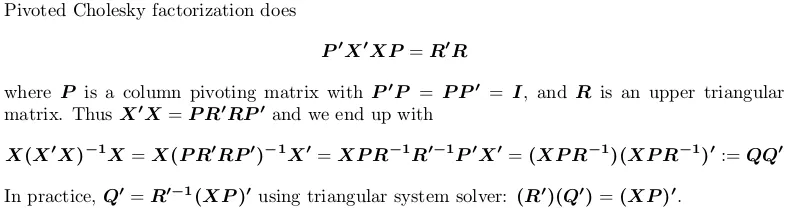
为了演示，我们仍然使用上面的示例X。

## pivoted Chol for `X'X`; we want lower triangular factor `L = R'`:
## we also suppress possible rank-deficient warnings (no harm at all!)
L <- t(suppressWarnings(chol(crossprod(X), pivot = TRUE)))

str(L)
# num [1:5, 1:5] 3.79 0.552 -0.82 -1.179 -0.182 ...
# - attr(*, "pivot")= int [1:5] 1 5 2 4 3
# - attr(*, "rank")= int 5

## compute `Q'`
r <- attr(L, "rank")
piv <- attr(L, "pivot")
Qt <- forwardsolve(L, t(X[, piv]), r)

## P = QQ'
H4 <- crossprod(Qt)

## compare
mean(abs(H1 - H4))
# [1] 6.983997e-17

再次，我们得到了相同的投影矩阵。

- Zheyuan Li

---

非常详细，特别是考虑到各种不同的方法。 - Erdogan CEVHER