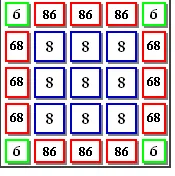
注意:开口应使用尽可能少的瓷砖来填充,表示较大的瓷砖具有优先权。
应该使用哪种算法进行瓷砖放置?
另一个示例。30 x 30的区域如下所示:

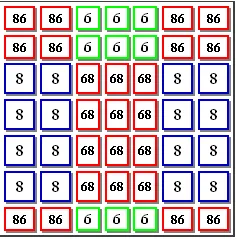



由于amit已经提供了通用案例答案,所以我将提供一个具体的解决方案。对于这四个块大小,假设它是可行的(尺寸为偶数且>=6等),您可以使用半贪心算法:
第一个目标是最大化8x8块的数量。为此,您需要确定每个方向需要多少个6大小的块。对于每个维度,只需检查是否可被8整除。如果不能被整除,则减去6。重复此过程直到可被整除(不应该超过3次)。
无论需要多少次,那就是您在该维度中需要的6x6块的数量。将它们组成一个矩形并放在一个角落里。从8x8块中再组成另一个矩形并将其放在相反的角落里。这两个矩形的角应该相互接触。
现在你可能会有一些剩余的空间,以两个相对角落的矩形的形式存在。我们知道每个矩形的一个维度可被8整除,另一个维度可被6整除。这里的简单方法是使用适当旋转的6x8方块来填充它,但这并不能保证最大数量的大型(8x8)方块。例如,对于50x50,你会剩下两个18x32的矩形。你可以用12个6x8瓷砖来填充它们。你甚至不能比12块更好,但你可以在那里放更多的8x8方块。
如果这不是一个问题,那么你就完成了(万岁)。这种方法的额外好处是你永远不需要使用4x8方块。
Blue - 8x8
Red - 6x6
Green - 6x8
Gray - 4x8


这里是Python代码:
def aux(x):
# in h we store the pre-calculated results for small dimensions
h = {18:[6,6,6], 16:[8,8], 14:[8,6], 12:[6,6], 10:[6,4], 8:[8], 6:[6], 4:[4]}
res = []
while x > 18:
# as long as the remaining space is large, we put there tiles of size 8
res.append(8)
x -= 8
if x not in h:
print("no solution found")
return []
return res + h[x]
def tiles( x, y ):
ax = aux(x) # split the x-dimension into tiles
ay = aux(y) # split the y-dimension into tiles
res = [ [ (x,y) for x in ax ] for y in ay ]
for u in res:
print(u)
return res
tiles( 30, 30 )
假设您正在寻找一般情况的答案,很抱歉要说 - 但这个问题是NP-Complete。它基本上是Subset Sum Problem的二维变体。
子集和问题:给定一个集合S和一个数字x - 找出是否存在一个子集S,其总和为x。
很容易看出,通过将子集和问题减少到大小为1*x的“字段”,并且对于S中的每个s,我们都有一个瓷砖1*s - 一个问题的解决方案也是另一个问题的解决方案。
因此 - 目前没有已知的多项式解决方案,大多数人认为不存在这样的解决方案。
但请注意,还有一种伪多项式动态规划解决方案子集和,在这里也可以使用。