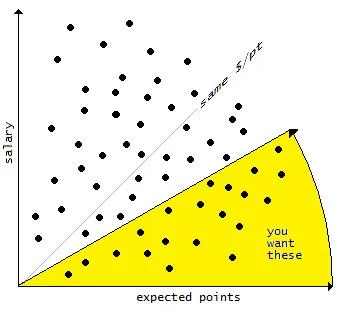
这是一个小有趣的项目,我开始尝试最大化赢得我们办公室冰球比赛的机会。我正在尝试找到在最大薪资帽下能给我带来最多积分的20名球员。
例如,假设原始数据由以下信息组成:
现在,显而易见的方法是简单地遍历所有可能的组合,然而,虽然这种方法可以实现目标,但对于500名球员来说,可能性太多了。我可以添加一些智能筛选器,将500名球员减少到前50名前锋、前30名后卫和前15名守门员,但仍然会非常缓慢。
我想知道是否有其他算法来实现这个目标。这只是为了好玩,并不是重要的商业请求。但如果你有任何想法,请让我知道。
我的第一次尝试是使用了背包算法和其他来源的帮助。它似乎只使用薪资作为参数就可以工作。但我很难弄清楚如何添加20名球员团队参数。它是用.Net实现的,但应该很容易转换成Java。
我在考虑做一个单独的循环,以找出最好的由20名球员组成的团队,而不考虑薪资,然后将两个列表进行比较,直到找到在两个列表中都排名最高的团队。不确定这样是否可行。
感谢您的帮助!
例如,假设原始数据由以下信息组成:
- 球员姓名
- 位置(前锋、后卫、守门员)
- 本赛季预计得分
- 薪资
现在,显而易见的方法是简单地遍历所有可能的组合,然而,虽然这种方法可以实现目标,但对于500名球员来说,可能性太多了。我可以添加一些智能筛选器,将500名球员减少到前50名前锋、前30名后卫和前15名守门员,但仍然会非常缓慢。
我想知道是否有其他算法来实现这个目标。这只是为了好玩,并不是重要的商业请求。但如果你有任何想法,请让我知道。
我的第一次尝试是使用了背包算法和其他来源的帮助。它似乎只使用薪资作为参数就可以工作。但我很难弄清楚如何添加20名球员团队参数。它是用.Net实现的,但应该很容易转换成Java。
我在考虑做一个单独的循环,以找出最好的由20名球员组成的团队,而不考虑薪资,然后将两个列表进行比较,直到找到在两个列表中都排名最高的团队。不确定这样是否可行。
namespace HockeyPoolCalculator
{
public class ZeroOneKnapsack
{
protected List<Item> itemList = new List<Item>();
protected int maxSalary = 0;
protected int teamSize = 0;
protected int teamSalary = 0;
protected int points = 0;
protected bool calculated = false;
public ZeroOneKnapsack() { }
public ZeroOneKnapsack(int _maxSalary)
{
setMaxSalary(_maxSalary);
}
public ZeroOneKnapsack(List<Item> _itemList)
{
setItemList(_itemList);
}
public ZeroOneKnapsack(List<Item> _itemList, int _maxSalary)
{
setItemList(_itemList);
setMaxSalary(_maxSalary);
}
// calculte the solution of 0-1 knapsack problem with dynamic method:
public virtual List<Item> calcSolution()
{
int n = itemList.Count;
setInitialStateForCalculation();
if (n > 0 && maxSalary > 0)
{
List<List<int>> playerList = new List<List<int>>();
List<int> salaryList = new List<int>();
//initialise list
playerList.Add(salaryList);
for (int j = 0; j <= maxSalary; j++)
salaryList.Add(0);
// Loop through players
for (int i = 1; i <= n; i++)
{
List<int> prev = salaryList;
playerList.Add(salaryList = new List<int>());
for (int j = 0; j <= maxSalary; j++)
{
if (j > 0)
{
int wH = itemList.ElementAt(i - 1).getSalary();
// Is the players salary more than the current calculated salary? If yes, then keep current max points, else get the highest amount between previous max points at that salary and new max points.
salaryList.Add((wH > j)?prev.ElementAt(j): Math.Max(prev.ElementAt(j),itemList.ElementAt(i - 1).getPoints() + prev.ElementAt(j - wH)));
}
else
{
salaryList.Add(0);
}
} // for (j...)
} // for (i...)
points = salaryList.ElementAt(maxSalary);
for (int i = n, j = maxSalary; i > 0 && j >= 0; i--)
{
int tempI = playerList.ElementAt(i).ElementAt(j);
int tempI_1 = playerList.ElementAt(i - 1).ElementAt(j);
if ((i == 0 && tempI > 0)||(i > 0 && tempI != tempI_1))
{
Item iH = itemList.ElementAt(i - 1);
int wH = iH.getSalary();
iH.setInKnapsack(1);
j -= wH;
teamSalary += wH;
}
} // for()
calculated = true;
} // if()
return itemList;
}
// add an item to the item list
public void add(String name, int Salary, int value)
{
if (name.Equals(""))
name = "" + (itemList.Count() + 1);
itemList.Add(new Item(name, Salary, value));
setInitialStateForCalculation();
}
// add an item to the item list
public void add(int Salary, int value)
{
add("", Salary, value); // the name will be "itemList.size() + 1"!
}
// remove an item from the item list
public void remove(String name)
{
for (int pointer = 0; pointer <= itemList.Count-1; pointer++)
{
itemList[pointer].getName().Equals("");
if (itemList.ElementAt(pointer).getName().Equals(itemList.ElementAt(pointer).getName()))
{
itemList.Remove(itemList.ElementAt(pointer));
}
}
setInitialStateForCalculation();
}
// remove all items from the item list
public void removeAllItems()
{
itemList.Clear();
setInitialStateForCalculation();
}
public int getPoints()
{
if (!calculated)
calcSolution();
return points;
}
public int getSolutionSalary() { return teamSalary; }
public bool isCalculated() { return calculated; }
public int getMaxSalary() { return maxSalary; }
public void setTeamSize(int _teamSize)
{
teamSize = _teamSize;
}
public int getTeamSize()
{
return teamSize;
}
public void setMaxSalary(int _maxSalary)
{
maxSalary = Math.Max(_maxSalary, 0);
}
public void setItemList(List<Item> _itemList) {
if (_itemList != null) {
itemList = _itemList;
foreach (Item item in _itemList) {
item.checkMembers();
}
}
}
// set the member with name "inKnapsack" by all items:
private void setInKnapsackByAll(int inKnapsack) {
foreach (Item item in itemList)
if (inKnapsack > 0)
item.setInKnapsack(1);
else
item.setInKnapsack(0);
}
// set the data members of class in the state of starting the calculation:
protected void setInitialStateForCalculation()
{
setInKnapsackByAll(0);
calculated = false;
points = 0;
teamSalary = 0;
teamSize = 0;
}
}
}
感谢您的帮助!