使用大O表示法证明N^2是O(2^N)

Question

使用大O表示法证明N^2是O(2^N)

big-oproof

9

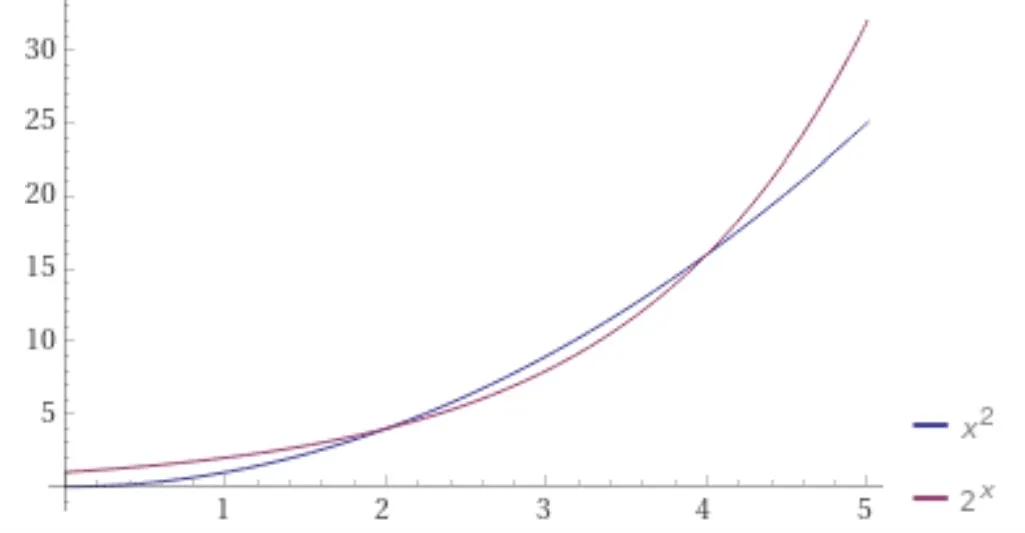
我可以清楚地看到N^2受c2^N的限制，但是如何使用大O符号的正式定义来证明它呢？我可以通过数学归纳法简单地证明它。

以下是我的尝试：根据定义，对于任何n>n0，存在一个常数C使得 f(n) <= Cg(n) 其中 f(n) = n^2 而 g(n) = 2^n

我应该对两边取对数并解出C吗？

还有一个关于斐波那契数列的问题，我想解决递归关系。

int fib(int n){
   if(n<=1) return n;
   else return fib(n-1) + fib(n-2);

The equation is..

T(n) = T(n-1)+T(n-2)+C // where c is for the adding operation

so

T(n) = T(n-2) + 2T(n-3) + T(n-4) + 3c

and one more

T(n) = T(n-3) + 3T(n-4) + 3T(n-5) + T(n-6) + 6c

then i started to get lost to form the general equation i The pattern is somehow like pascal triangle?

 t(n) = t(n-i) + aT(n-i-1) + bT(n-i-2) + ... + kT(n-i-i) + C

- Timothy Leung

1

最好在这里询问。 - wap26

那么我应该在这里删除这篇文章吗？ - Timothy Leung

1

一种方法是使用当n趋近于无穷大时g(n)/f(n)的极限。 - Adam

您介意能否详细解释一下吗？当 n 趋近于无穷大时，2^n / n^2 会比 n^2 生长得更快，因此 g(n)/f(n) 也会趋近于无穷大，对吗？ - Timothy Leung

3个回答

2

大部分来说，被接受的答案（来自aioobe）是正确的，但是有一个需要做出重要更正。

是的，对于x=2，2×log(x) = x 或者 2×log(2) = 2 是正确的，但是他错误地暗示了 2×log(x) < x 对于所有的x>2 都成立，这是不正确的。

我们可以取x=3，这样方程就变成了：2×log(3) < 3 （一个无效的方程）。

如果你计算一下，你会得到：2×log(3) ≈ 3.16993，大于3。

如果你绘制 f(x) = x² 和 g(x) = 2^x 或者你绘制 f(x)= 2×log(x) 和 g(x) = x（如果c=1），你就可以清楚地看到这一点。

在x=2和x=4之间，你可以看到g(x)会下降到低于f(x)。只有当x≥4时，f(x)才会保持≤c×g(x)。为了得到正确的答案，按照aioobe的答案所述的步骤进行操作，但是绘制函数以获取最后一个交点，在那个交点处，f(x)=c×g(x)。该交点的x值是你的x0（与所选的c一起），对于所有x≥x0，以下条件成立：f(x)≤c×g(x)。因此，对于c=1，应为：对于所有x≥4，或者x0=4。

- Fishezzz

0

为改进接受的答案：

您必须证明对于所有x > 2，x^2 < 2^x

在两边取对数，我们必须证明： 2·log(x) < x 对于所有x > 2

因此，我们必须展示函数h(x)=x-2·log(x)>0对于所有x>2

h(2)=0

对h(x)进行微分，得到h'(x)= 1 - 1/(x·ln(2))

对于所有x>2，h'(x)始终大于0，因此h(x)不断增加，由于h(2)=0，因此已经证明了h(x) > 0对于所有x > 2，或者说对于所有x > 2，x^2 < 2^x

- naman

网页内容由stack overflow 提供, 点击上面的

可以查看英文原文，
原文链接

- aioobe · Accepted Answer

正如您所指出的，要确定 f(x) ϵ O(g(x))，您需要找到：

一些 c > 0
一些 x₀

使得对于所有 x > x₀ 都满足 f(x) < c·g(x)。

在这种情况下，您可以选择 c = 1，x₀ = 2。您需要证明的是： x² < 2^x 对于所有 x > 2 均成立。

此时，您可以取两边的对数（因为如果 log(x) > log(y)，则 x > y）。假设您使用底数为2的对数，则可得到以下结果： log(x²) < log(2^x) 根据对数的标准法则，您可以得到： 2·log(x) < x·log(2) 由于 log(2) = 1，因此可将其写作： 2·log(x) < x 如果我们将 x 设为2，则有： 2·log(2) = 2

由于 x 的增长速度大于 log(x)，因此我们知道 2·log(x) < x 对所有 x > 2 都成立。