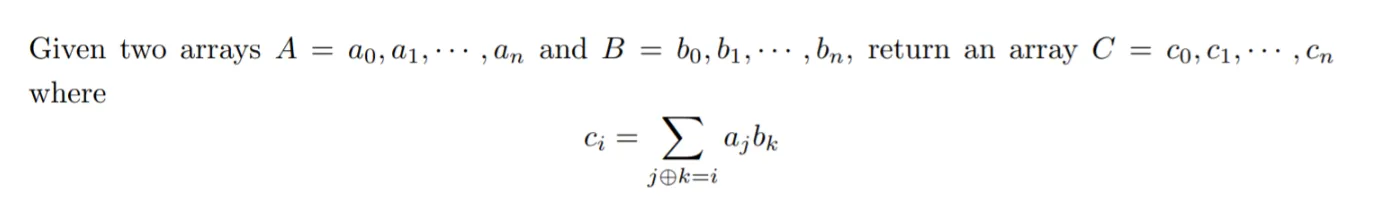如何优化这个XOR求和算法？

Question

我正在尝试解决这个 Hackerrank 的问题 https://www.hackerrank.com/challenges/xor-subsequence/problem。

from functools import reduce

def xor_sum(arr):
    return reduce(lambda x,y: x^y, arr)    

def xorSubsequence(arr):
    freq = {}
    max_c = float("-inf") # init val
    min_n = float("inf") # init val
    
    for slice_size in range(1, len(arr)+1):
        for step in range(0, len(arr)+1-slice_size):
            n = xor_sum(arr[i] for i in range(step,step+slice_size))
            
            freq[n] = freq.get(n,0)+1
            if freq[n] >= max_c and (n < min_n or freq[n]> max_c):
                min_n = n
                max_c = freq[n]

    return  min_n, freq[min_n]

但是由于它的时间复杂度为O(n^3)，所以超时了。 我感觉有一些数学技巧，有人能解释一下解决方案吗？我尝试阅读了一些讨论中的解决方案，但是我没有完全理解。

考虑一个包含n个整数（A=a0,a1,...,an-1）的数组A。我们取数组中满足以下条件的所有连续子序列： {ai,ai+1,...,aj-1,aj}，其中0≤i≤j≤n。

对于每个子序列，我们对所有整数应用按位异或（⊕）操作，并记录结果值。

给定数组A，找到A的每个子序列的异或和，并确定每个数字出现的频率。然后将数字和其相应的频率作为两个以空格分隔的值打印在同一行上。

输出格式：

在单独的一行上打印两个以空格分隔的整数。 第一个整数应该是具有最高频率的数字， 第二个整数应该是该数字的频率（即它出现的次数）。 如果有多个具有最大频率的数字， 选择最小的一个。

约束条件：

• 1≤n≤105 • 1≤ai<216

- Axeltherabbit

---

哦，哇。我自己还没有完全理解它，但显然这是关键：https://en.wikipedia.org/wiki/Fast_Walsh%E2%80%93Hadamard_transform - Kache

Answer 1

该解决方案使用了两个技巧。

第一个技巧是计算n + 1个前缀和σ [0]，…，σ [n]（正如所指出的），但是使用XOR而不是+（例如，σ [2] = a [0] XOR a [1] XOR a [2]）。从i到j的子列表的XOR和等于σ [i-1] XOR σ [j]。如果我们将i-1和j循环遍历所有可能的值0，…，n而不考虑约束条件i ≤ j，则每个子列表都会有两次（一次“向前”，一次“向后”），并且还会有n + 1个额外的零，即当i-1 = j时。

第二个技巧是快速沃尔什-哈达玛变换可以在O（n log n）时间内解决以下问题：给定列表X和列表Y，我们希望找到（x，y）的频率计数，其中（x，y）∈ X × Y。 （对于此问题，X = Y，但如果使用单独的变量，则此技巧的结构更清晰。）为什么我们应该怀疑首先存在快速算法？除了极限之外，如果是x + y而不是x XOR y，那么我们将寻求快速乘多项式。

让我们用其频率向量f替换列表X，并用其频率向量g替换列表Y。例如，X = [0, 0, 0, 2, 2, 3]变为f = [3, 0, 2, 1]。假设f和g有四个元素，则期望的结果是

[f[0] g[0] + f[1] g[1] + f[2] g[2] + f[3] g[3]
,f[0] g[1] + f[1] g[0] + f[2] g[3] + f[3] g[2]
,f[0] g[2] + f[1] g[3] + f[2] g[0] + f[3] g[1]
,f[0] g[3] + f[1] g[2] + f[2] g[1] + f[3] g[0]
].

这是一个称为对称双线性形式的代数对象示例，意味着存在某个基变换矩阵B使得所需结果为B⁻¹ (B f * B g)，其中*表示逐元素乘法。(剧透：B是Walsh矩阵。)

为了对快速沃尔什-哈达玛变换产生直观感受，它可以高效地计算出每个向量v的B v，让我展示一下当我将结果的前两个元素相加时会发生什么:

f[0] g[0] + f[1] g[1] + f[2] g[2] + f[3] g[3]
+ f[0] g[1] + f[1] g[0] + f[2] g[3] + f[3] g[2]
= f[0] (g[0] + g[1]) + f[1] (g[1] + g[0]) + f[2] (g[2] + g[3]) + f[3] (g[3] + g[2])
= (f[0] + f[1]) (g[0] + g[1]) + (f[2] + f[3]) (g[2] + g[3])

并添加后两个元素：

f[0] g[2] + f[1] g[3] + f[2] g[0] + f[3] g[1]
+ f[0] g[3] + f[1] g[2] + f[2] g[1] + f[3] g[0]
= f[0] (g[2] + g[3]) + f[1] (g[3] + g[2]) + f[2] (g[0] + g[1]) + f[3] (g[1] + g[0])
= (f[0] + f[1]) (g[2] + g[3]) + (f[2] + f[3]) (g[0] + g[1])

并减去前两个元素：

f[0] g[0] + f[1] g[1] + f[2] g[2] + f[3] g[3]
− (f[0] g[1] + f[1] g[0] + f[2] g[3] + f[3] g[2])
= f[0] (g[0] − g[1]) + f[1] (g[1] − g[0]) + f[2] (g[2] − g[3]) + f[3] (g[3] − g[2])
= (f[0] − f[1]) (g[0] − g[1]) + (f[2] − f[3]) (g[2] − g[3])

并减去第二个和第三个元素：

f[0] g[2] + f[1] g[3] + f[2] g[0] + f[3] g[1]
− (f[0] g[3] + f[1] g[2] + f[2] g[1] + f[3] g[0])
= f[0] (g[2] − g[3]) + f[1] (g[3] − g[2]) + f[2] (g[0] − g[1]) + f[3] (g[1] − g[0])
= (f[0] − f[1]) (g[2] − g[3]) + (f[2] − f[3]) (g[0] − g[1]) .

如果我们令 f′ = [f[0] + f[1], f[2] + f[3]] 和 g′ = [g[0] + g[1], g[2] + g[3]]，那么前两个量是 [f′[0] g′[0] + g′[1] g′[1], f′[0] g′[1] + f′[1] g′[0]]，这与原问题相同但规模减半。第二个两个量也是如此，最后我们可以恢复原问题。

x = f[0] g[0] + f[1] g[1] + f[2] g[2] + f[3] g[3]
y = f[0] g[1] + f[1] g[0] + f[2] g[3] + f[3] g[2]

通过 x + y 和 x - y 得到 x = ((x + y) + (x - y))/2 和 y = ((x + y) - (x - y))/2 （对于所有其他成对的也同理）。请注意，Kache 的代码将除法推迟到最后，以便可以重用相同的转换。

- David Eisenstat

Answer 2

请注意，您的算法不是O(n²)，而是O(n³)，但是您可以通过将每个新数字与上一个“切片”的所有结果（加上该数字本身，开始一个新的子序列）进行异或运算，将其降低到O(n²)。

from collections import Counter
def xor_sub_sum(arr):
    freq = Counter()
    last = []
    for x in arr:
        last = [x, *(x^y for y in last)]
        freq.update(last)
    # "most_common" does not consider smallest-key constraint...
    return max(freq.items(), key=lambda t: (t[1], -t[0]))

在我的机器上，这将1000个元素的执行时间从21.7秒减少到仅为0.05秒。对于10000个元素，尽管如此，仍需要约5秒钟的时间。

- tobias_k

---

优化得不错，但在大型测试用例上仍然会超时。 - Axeltherabbit

Answer 3

好的，我还是不完全理解它，但是通过根据维基百科的描述实现一个基于 O(n log(n)) 的 fwht() 函数，并从另一个现有的解决方案中获取信息，我能够通过所有测试：

from collections import Counter
from itertools import accumulate
from operator import xor


def fwht(arr):
    # https://en.wikipedia.org/wiki/Fast_Walsh%E2%80%93Hadamard_transform
    if len(arr) == 1:
        return arr

    prefix, suffix = arr[:len(arr) // 2], arr[len(arr) // 2:]

    new_prefix = fwht([p + s for p, s in zip(prefix, suffix)])
    new_suffix = fwht([p - s for p, s in zip(prefix, suffix)])
    return new_prefix + new_suffix


def xorSubsequence(seq):
    next_pow2 = 2**(len(seq) - 1).bit_length()

    histogram = Counter(accumulate([0] + seq, xor))
    histogram = [histogram[value] for value in range(next_pow2)]

    histogram = [x * x for x in fwht(histogram)]
    histogram = [y // next_pow2 for y in fwht(histogram)]

    histogram[0] -= len(seq) + 1             # self combos (diagonal in table)
    histogram = [y // 2 for y in histogram]  # don't count things twice

    max_freq = max(histogram)
    return next((i, freq) for i, freq in enumerate(histogram) if freq == max_freq)

- Kache

---

非常感谢，我会在几天内添加悬赏以查看是否有人能够提供解释。 - Axeltherabbit

next_pow2 应该是 2**max(seq).bit_length()。 - Stanislav Volodarskiy

Answer 4

为什么异或和是二元卷积

将输入数组表示为a。

构造一个数组b，使得b[i]=a[0]⊕a[1]⊕...⊕a[i]。然后构建一个列表M，其中M[i]表示值为i的元素在b中出现的次数。注意，为了使M的长度成为2的幂，添加了一些零填充。

然后考虑二元（XOR）卷积。定义如下（图片来自此问题）：

考虑在M和M之间进行此二元卷积，即N=M*M，其中*表示二元卷积。那么N[i]是所有(j,k)的M[j]M[k]之和，其中j⊕k=i。

考虑每个子序列xor(a[p:q])，我们有xor(a[p:q])=b[p]⊕b[q]。对于每个整数i，所有连续的子序列的异或结果都相等，可以转换为这种形式（i=xor(a[p:q])=b[p]⊕b[q]）。我们进一步通过b[p]和b[q]的值将这个子序列族分组，例如，如果xor(a[p1:q1])=xor(a[p2,q2])=i，并且如果b[p1]=b[p2],b[q1]=b[q2]，则这两个子序列将被分组到同一个子组中。考虑子组(j,k)，其中子序列可以表示为i=xor(a[p':q'])=b[p']⊕b[q'], b[p']=j, b[q']=k，该子组中的子序列数为M[j]M[k]（回想一下，M[i]表示值为i的元素在b中出现的次数）。因此，N[i]是xor(a[p:q])=i的子序列数。

然而，由于 a[p:q] 和 a[q:p] 是相同的，我们会将每个子序列都计算两次。因此，N[i] 是“连续子序列异或得到 i 的数量”的两倍。

使用 FWHT 计算卷积

现在我们需要计算 N=M*M，根据 Dyadic(XOR) 卷积定理 (参见证明这里)，我们可以先计算 H(N)=H(M)×H(M)。由于 H 是可逆的(参见 wiki)，要得到 N 只需再次对 H(N) 应用 H。

代码分析

在这一部分中，我将分析由 @Kache 提供的代码。

实际上，b 是 accumulate([0] + seq, xor)。使用 histogram = Counter(accumulate([0] + seq, xor))，可以获得一个字典 {b 中可能的值: 出现次数}。然后下一行，histogram = [histogram[value] for value in range(next_pow2)]，这就是上文提到的加上填充后的 M。

然后，在 histogram = [x * x for x in fwht(histogram)] 中，现在直方图是 H(N)。而 histogram = [y // next_pow2 for y in fwht(histogram)] 则用作逆变换。

这就是 histogram = [y // next_pow2 for y in fwht(histogram)] 的作用。 histogram[0] -= len(seq) + 1 消除了 a[p:p]=0 的影响。而 histogram = [y // 2 for y in histogram] 则避免了计算两次（如前所述，N[i] 将 a[p:q] 和 a[q:p] 分别计算）。

- hellohawaii

Answer 5

我提议将这作为索引 l 和 r 之间子序列的功能异或和。

# Sequence (An)n is defined by A(n)=A(n-1)^n with ^ bitwise xor operation
# Compute bitwise xor of subsequence of consecutive sequence elements
# ...between a left and right index, A(k), k=l..r, i.e., A(l)^A(l+1)^...^A(r-1)^A(r)

#!/bin/python3

import math
import os
import random
import re
import sys

# Hints ##
# Notice how to bitwise xor of consecutive integers in range 1..n simplifies
# e.g., printing out bitwise xor of consecutive integers in 1..13
# 0 1 3 0 4 1 7 0 8 1 11 0 12
# ...someting happens, some pattern wrt n%4
# Method comp_xor_in_range(n) shows a corresponding fast implementation
# for bitwise xor of consecutive integers in range 1..n

# Then, notice how bitwise xor of (An)n subsequence elements simplifies, depending on 
# ...parity of left index and parity of number of elements in subsequence 

# compute bitwise xor of elements in range 1..n
def comp_xor_in_range(l):
    res=l%4
    if res==0:
        return l
    elif res==1:
        return 1
    elif res==2:
        return l+1
    else:
        return 0

# compute bitwise xor of elements in range l(eft)..r
def comp_xor_in_range_lr(l,r):
    return comp_xor_in_range(l-1)^comp_xor_in_range(r)

#compute bitwise xor of even elements in range 1..n 
def comp_xor_even_in_range(l):
    res=l%2
    if res==0:
        return 2*comp_xor_in_range(l//2)
    else:
        return 2*comp_xor_in_range((l-1)//2)
    
# compute bitwise xor of even elements in range l(eft)..r
def comp_xor_even_in_range_lr(l,r):
    return comp_xor_even_in_range(l-1)^comp_xor_even_in_range(r)

#compute bitwise xor of odd elements in range 1..n 
def comp_xor_odd_in_range(l):
    return comp_xor_even_in_range(l)^comp_xor_in_range(l)

# compute bitwise xor of even elements in range l(eft)..r
def comp_xor_odd_in_range_lr(l,r):
    return comp_xor_odd_in_range(l-1)^comp_xor_odd_in_range(r)

def xorSequence(l, r):
    n=r-l+1
    
    if n%2==0:
        if l%2==0:
            return comp_xor_odd_in_range_lr(l,r)
        else:
            return comp_xor_even_in_range_lr(l,r)
    else:
        if l%2==0:
            return comp_xor_even_in_range_lr(l+1,r)^comp_xor_in_range(l)
        else:
            return comp_xor_odd_in_range_lr(l+1,r)^comp_xor_in_range(l)


    
if __name__ == '__main__':
    fptr = open(os.environ['OUTPUT_PATH'], 'w')

    q = int(input())

    for q_itr in range(q):
        lr = input().split()

        l = int(lr[0])

        r = int(lr[1])

        result = xorSequence(l, r)

        fptr.write(str(result) + '\n')

    fptr.close()

- kiriloff

---

这与问题有什么关系？ - Kelly Bundy

它准确地解决了问题，也许这就足够了。 - kiriloff

绝对不是这样。你甚至都没有正确阅读输入。你假装存在 l/r 对而不是数组值。 - Kelly Bundy

嗯，任何有大脑和十根手指的人都可以稍微整理一下。 - kiriloff

怎么做呢？你的解决方案依赖于数组值具有特定的模式，对吗？那么如何“稍微调整”它，以便能够解决问题中的任意数组值呢？ - Kelly Bundy