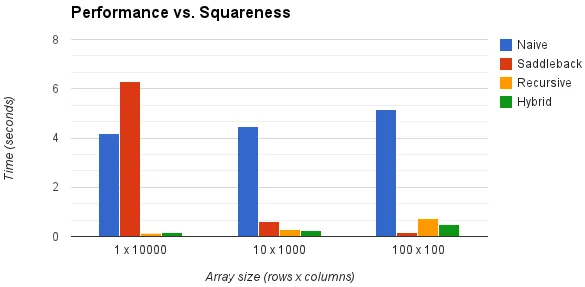
到目前为止,两个最主要的答案似乎是具有争议的 O(log N) 的 "ZigZag方法" 和 O(N+M) 的二分查找方法。我想做一些测试来比较这两种方法在不同情况下的表现。以下是详细信息:数组在每个测试中都是一个 N x N 的正方形,其中 N 从 125 变化到 8000(这是我的 JVM 堆可以处理的最大值)。对于每个数组大小,我选了一个随机位置在数组中放置一个单独的 2。然后将 3 放置到可能的所有位置 (2 的右侧和下面),然后将剩余的数组用 1 填充。之前的评论者中一些人认为这种设置会导致两种算法的最坏运行时间。对于每个数组大小,我选择了 100 个不同的随机位置作为搜索目标并运行了测试。我记录了每个算法的平均运行时间和最坏运行时间。由于在 Java 中发生得太快,以至于无法获得良好的毫秒读数,并且因为我不信任 Java 的 nanoTime(),我重复了每个测试 1000 次,以增加所有时间的统一偏差因子。以下是结果。ZigZag 在每个测试中击败了二进制,无论是平均时间还是最坏情况时间,但它们都在同一个数量级内。以下是 Java 代码:
public class SearchSortedArray2D {
static boolean findZigZag(int[][] a, int t) {
int i = 0;
int j = a.length - 1;
while (i <= a.length - 1 && j >= 0) {
if (a[i][j] == t) return true;
else if (a[i][j] < t) i++;
else j--;
}
return false;
}
static boolean findBinarySearch(int[][] a, int t) {
return findBinarySearch(a, t, 0, 0, a.length - 1, a.length - 1);
}
static boolean findBinarySearch(int[][] a, int t,
int r1, int c1, int r2, int c2) {
if (r1 > r2 || c1 > c2) return false;
if (r1 == r2 && c1 == c2 && a[r1][c1] != t) return false;
if (a[r1][c1] > t) return false;
if (a[r2][c2] < t) return false;
int rm = (r1 + r2) / 2;
int cm = (c1 + c2) / 2;
if (a[rm][cm] == t) return true;
else if (a[rm][cm] > t) {
boolean b1 = findBinarySearch(a, t, r1, c1, r2, cm - 1);
boolean b2 = findBinarySearch(a, t, r1, cm, rm - 1, c2);
return (b1 || b2);
} else {
boolean b1 = findBinarySearch(a, t, r1, cm + 1, rm, c2);
boolean b2 = findBinarySearch(a, t, rm + 1, c1, r2, c2);
return (b1 || b2);
}
}
static void randomizeArray(int[][] a, int N) {
int ri = (int) (Math.random() * N);
int rj = (int) (Math.random() * N);
a[ri][rj] = 2;
for (int i = 0; i < N; i++) {
for (int j = 0; j < N; j++) {
if (i == ri && j == rj) continue;
else if (i > ri || j > rj) a[i][j] = 3;
else a[i][j] = 1;
}
}
}
public static void main(String[] args) {
int N = 8000;
int[][] a = new int[N][N];
int randoms = 100;
int repeats = 1000;
long start, end, duration;
long zigMin = Integer.MAX_VALUE, zigMax = Integer.MIN_VALUE;
long binMin = Integer.MAX_VALUE, binMax = Integer.MIN_VALUE;
long zigSum = 0, zigAvg;
long binSum = 0, binAvg;
for (int k = 0; k < randoms; k++) {
randomizeArray(a, N);
start = System.currentTimeMillis();
for (int i = 0; i < repeats; i++) findZigZag(a, 2);
end = System.currentTimeMillis();
duration = end - start;
zigSum += duration;
zigMin = Math.min(zigMin, duration);
zigMax = Math.max(zigMax, duration);
start = System.currentTimeMillis();
for (int i = 0; i < repeats; i++) findBinarySearch(a, 2);
end = System.currentTimeMillis();
duration = end - start;
binSum += duration;
binMin = Math.min(binMin, duration);
binMax = Math.max(binMax, duration);
}
zigAvg = zigSum / randoms;
binAvg = binSum / randoms;
System.out.println(findZigZag(a, 2) ?
"Found via zigzag method. " : "ERROR. ");
System.out.println("max search time: " + zigMax + "ms");
System.out.println("avg search time: " + zigAvg + "ms");
System.out.println();
System.out.println(findBinarySearch(a, 2) ?
"Found via binary search method. " : "ERROR. ");
System.out.println("max search time: " + binMax + "ms");
System.out.println("avg search time: " + binAvg + "ms");
}
}