高效计算卢卡斯序列

Question

我正在实现 p+1 分解算法。为此，我需要计算 lucas 序列的元素，该序列由以下定义：

Lucas(n) = 0 if n=0, Lucas(1) = 1, Lucas(n) = P*Lucas(n-1) - Q*Lucas(n-2)

(1) x_0 = 1, x_1 = a
(2) x_n+l  =  2 * a * x_n - x_n-l

我用递归实现了它（使用C#），但对于较大的索引来说效率不高。

static BigInteger Lucas(BigInteger a, BigInteger Q, BigInteger N)
    {
        if (Q == 0)
            return 1;
        if (Q == 1)
            return a;
        else
            return (2 * a * Lucas(a, Q - 1, N) - Lucas(a, Q - 2, N)) % N;
    }

我也知道。

(3) x_2n = 2 * (x_n)^2 - 1
(4) x_2n+1 = 2 * x_n+1 * x_n - a
(5) x_k(n+1) = 2 * x_k * x_kn - x_k(n-1)

(3)和(4)应该有助于计算更大的Q。但我不确定如何做。

我认为可以使用Q的二进制形式来实现。

非常感谢您的帮助。

- ArtVandelay

---

针对这种任务，您可以使用记忆化来避免重复计算相同的子结果。此外，研究使用基于堆的堆栈来跟踪进度，而不是递归--这可以防止StackOverflowExceptions，并通过减少堆栈上的翻转来提高性能。 - Drew Noakes

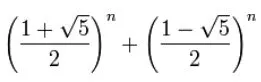
计算模N的事实可能会很有用。对于N的值是否有其他限制吗？ - Samuel Edwin Ward

N是一个正的非质数。我认为解决方案在这里的第三段话中：http://programmingpraxis.com/2010/06/04/williams-p1-factorization-algorithm/。但是我难以理解并将其转化为代码。 - ArtVandelay

Answer 1

这里 可以看到如何使用矩阵乘方来找到第N个斐波那契数。

      n
(1 1)
(1 0)

你可以利用这种方法来计算卢卡斯数，使用矩阵（对于你的情况 x_n+l = 2 * a * x_n - x_n-l）。

        n
(2a -1)
(1   0)

注意，可以通过平方法进行log(N)次矩阵乘法来找到矩阵的N次方。

- MBo

Answer 2

(3) x_2n = 2 * (x_n)^2 - 1
(4) x_2n+1 = 2 * x_n+1 * x_n - a

每当你看到2n，你应该想到“那可能表示一个偶数”，同样的2n+1可能意味着“那是一个奇数”。

你可以修改x索引，使得左边有n（以便更容易理解它如何对应递归函数调用），但要注意四舍五入。

3) 2n     n
=> n      n/2

4) it is easy to see that if x = 2n+1, then n = floor(x/2)
     and similarly n+1 = ceil(x/2)

所以，对于第三个问题，我们有以下伪代码：

if Q is even
   return 2 * (the function call with Q/2) - 1

而对于 #4：

else // following from above if
   return 2 * (the function call with floor(Q/2))
            * (the function call with ceil(Q/2)) - a

然后我们还可以加入一些记忆化以防止对相同参数计算返回值多次：

• 保持一个从Q值到返回值的映射。
• 在函数开始时，检查映射中是否存在Q的值。如果存在，则返回对应的返回值。
• 返回时，将Q的值和返回值添加到映射中。

- Bernhard Barker

---

这实际上导致了一个O(log n)算法，这并不是显而易见的。 - Niklas B.

Answer 3

你可以在不使用非常复杂的数学方法的情况下获得一些改进（只是百万分之一...）。

首先，让我们更明确地描述数据流：

    static BigInteger Lucas(BigInteger a, BigInteger Q, BigInteger N)
    {
        if (Q == 0)
        {
            return 1;
        }
        else if (Q == 1)
        {
            return a;
        }
        else
        {
            BigInteger q_1 = Lucas(a, Q - 1, N);
            BigInteger q_2 = Lucas(a, Q - 2, N);
            return (2 * a * q_1 - q_2) % N;
        }
    }

毫不意外，这并没有真正改变性能。

然而，这确实表明我们只需要两个先前的值来计算下一个值。这使我们可以将函数倒置为迭代版本：

    static BigInteger IterativeLucas(BigInteger a, BigInteger Q, BigInteger N)
    {
        BigInteger[] acc = new BigInteger[2];
        Action<BigInteger> push = (el) => {
                acc[1] = acc[0];
                acc[0] = el;
        };
        for (BigInteger i = 0; i <= Q; i++)
        {
            if (i == 0)
            {
                push(1);
            }
            else if (i == 1)
            {
                push(a);
            }
            else
            {
                BigInteger q_1 = acc[0];
                BigInteger q_2 = acc[1];
                push((2 * a * q_1 - q_2) % N);
            }
        }
        return acc[0];
    }

可能有一种更清晰的写法，但它是有效的。而且速度快得多。它的速度非常快，以至于测量起来有点不切实际。在我的系统上，Lucas(4000000, 47, 4000000)花费了大约30分钟，而IterativeLucas(4000000, 47, 4000000)只花费了大约2毫秒。我想比较48，但我没有耐心。

您可以使用模算术的这些属性挤出更多（也许是两倍的因子？）：

(a + b) % n = (a%n + b%n) % n
(a * b) % n = ((a%n) * (b%n)) % n

如果你应用这些方法，你会发现a％N出现了几次，所以在循环之前预先计算一次就可以赢得胜利。当a比N大得多时，这尤其有帮助；我不确定这是否适用于你的应用程序。

可能有一些巧妙的数学技巧可以轻松解决这个问题，但我认为通过稍微调整一下代码就可以实现这样的改进是很有趣的。

- Samuel Edwin Ward

Answer 4

第n个卢卡斯数的值为：

平方求幂法可用于计算该函数。例如，如果n=1000000000，则n = 1000 * 1000^2 = 10 * 10^2 * 1000^2 = 10 * 10^2 * (10 * 10^2 )^2。通过这种简化方式，您可以大大减少计算次数。

- Tyler Durden