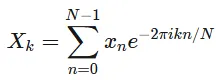为什么 FFT 会生成复数而不是实数？

Question

所有我们接触到的FFT实现都会返回复数值（由实部和虚部组成），即使该算法的输入是一个离散的实数集合（整数）。

是否不可能仅使用实数来表示频域？

- steve landiss

Answer 1

FFT基本上是一种变换基的方法。FFT将原始信号变换为正弦波的一组基。为了使该基能够描述所有可能的输入，它需要能够表示相位和幅度; 相位使用复数表示。

例如，假设您对仅包含单个正弦波的信号进行FFT。根据相位，您可能会得到完全实际的FFT结果。但是，如果您将输入的相位移动几度，FFT输出如何表示该输入？

编辑：这是一个有些宽松的解释，但我只是试图激发直觉。

- zmccord

---

它有助于回答很多问题。如果FFT结果仅包含频率和相位信息，在时间域采样中如何捕获振幅信息？也就是说，在iFFT中如何重新创建正确的振幅？ - steve landiss

每个FFT中的值对应一个不同的频率分量。该值的幅度是该分量的振幅，而复角是该分量的相位。 - zmccord

Answer 2

FFT 提供振幅和相位。振幅被编码为复数的大小（sqrt(x^2+y^2)），而相位被编码为角度（atan2(y,x)）。为了从 FFT 中获得严格实数结果，输入信号必须具有偶对称性（即 x[n]=conj(x[N-n])）。

如果您只关心强度，则复数的大小足以进行分析。

- antijon

Answer 3

是的，使用实数就可以表示严格实输入的FFT频域结果。

在FFT结果中，那些复数实际上只是由两个实数组成，这两个实数都是必需的，才能给出一个具有长度和方向角度（或幅度和相位）的结果向量的二维坐标。每个频率分量在FFT结果中都可以具有独特的振幅和独特的相位（相对于FFT孔径中的某一点）。

单独的一个实数无法同时表示幅值和相位。如果舍弃相位信息，这可能会导致信号严重失真，尤其是当你尝试使用iFFT重新创建该信号时，而该信号并不对称。因此，每个FFT bin需要两个实数来完整表示FFT结果。这两个实数在某些FFT中被捆绑在一起，形成一个常见的复杂数据类型，但是FFT结果可以很容易地（并且一些FFT确实如此）生成两个实向量（一个余弦坐标向量和一个正弦坐标向量）。

还有一些FFT例程直接产生幅度和相位，但是它们的运行速度比生成复杂（或两个实数）向量结果的FFT要慢。还有一些FFT例程仅计算幅度并直接舍弃相位信息，但它们通常运行速度不比让你自己在更一般的FFT之后转换或忽略需要或不需要的内容要快。也许它们可以省去程序员几行代码，但代价是不可逆。但是很多库不费力地包含这些更慢和不太通用的FFT形式，并且只让程序员转换或忽略他们需要或不需要的内容。

此外，许多人认为使用复数算术进行求解的数学更加优雅（其中，对于严格实输入，在FFT结果的实部中放置余弦相关性甚至分量，在虚部中放置正弦相关性或奇数分量）。

（添加：）另一个选项是将每个FFT结果bin的两个组件视为偶数和奇数组件，都是实数，而不是实部和虚部。

- hotpaw2

Answer 4

如果给定频率f的FFT系数为x + i y，则可以将x视为该频率上余弦波的系数，而y是正弦波的系数。如果将这两个波加在一起，则会得到一个相移后的波，其频率为该特定频率；此波的幅度为sqrt(x*x + y*y)，等于复系数的幅度。

离散余弦变换（DCT）是傅里叶变换的一种相关形式，它产生所有实系数。许多图像/视频压缩算法使用二维DCT。

- comingstorm

Answer 5

1. 离散傅里叶变换（DFT）从一组复数向量在“时域”内转换为一组复数向量在“频域”内（使用正确的缩放因子，DFT可自行反演）。如果输入是实数，则可以同时执行两个DFT：取输入向量x和y并计算F（x+i y）。我忘记了如何分离DFT，但我猜这涉及到对称性和共轭复数。

2. 离散余弦变换让你将“频域”表示为实数，在有损压缩算法（JPEG，MP3）中很常见。令人惊讶的是它即使看起来丢失了相位信息也能正常工作，但这似乎使它对大多数信号处理目的不太有用（我不知道如何用DCT进行卷积/相关）。

我可能有些细节理解错误 ;)

- tc.

---

我很想了解更多关于你所说的“之后分离DFT”的信息，特别是对于变换F(x + i y)的情况。 - CatsLoveJazz

Answer 6

根据您提问的用语，我认为您正在寻找一种更直观的思考方式，而不是数学解答。我来自机械工程背景，这是我理解傅里叶变换的方式。我将傅里叶变换与摆锤相联系。如果我们只有摆锤在时间上的速度与位置之间的关系，被要求估计摆锤的能量（或摆锤的推力源），傅里叶变换可以给出一个完整的答案。通常情况下，我们只观察到了摆锤的速度，可能会得出结论：只需要向摆锤提供等于其动能正弦变化的能量就足够了。但摆锤也具有势能。这种能量与势能相位差90度。因此，为了跟踪势能，我们只需要保留（动）实部中的90度相位差部分。虚部可以被视为“势速度”，代表了源必须提供的势能的体现，以引起振荡行为。有帮助的是，这种方法可以很容易地扩展到电气背景下，电容器和电感器也以“潜在形式”存储能量。当信号不是正弦信号时，变换会尝试将其分解成正弦信号。这就好像假设最终信号是由无限源的组合行为产生的，每个源都具有不同的正弦行为。我们试图确定每个源在每个时间瞬间创建了最终观察到的信号的强度和相位。

注：1）最后两个陈述通常是我对傅里叶变换本身的理解。 2）我说“势速度”而不是潜在能量，因为变换通常不改变原始信号或物理量的维度，因此不能从表示速度转变为能量。

- JBR

---

有两个来源可以正确解释傅里叶变换并详细说明傅里叶变换公式。 [3Blue1Brown的一段视频]（https://www.youtube.com/watch?v=spUNpyF58BY）（他已经很好地揭开了许多数学和物理概念的神秘面纱），以及Elan Ness-Cohn制作的带有动画的页面，适当地标题为：发展对傅里叶变换的直觉。两者都是高质量的解释，给出了原理的详尽视角。 - mins

Answer 7

简答：

短回答

FFT 为什么会产生复数而不是实数？

FT 结果为复数数组的原因在于系数计算中涉及到了复指数乘法器。最终结果因此为复数。FT 使用该乘法器来将信号与多个频率进行相关性分析。原理在下文中进一步详述。

不能用实数表示频域吗？

当然，FT 返回的复系数的 1D 数组可以用由实值构成的 2D 数组来表示，这可以是笛卡尔坐标 x 和 y，也可以是极坐标 r 和 θ（更多 信息）。但是...

复指数形式是信号处理中最适合的形式

仅有实数据并不是很有用。

一方面，已经可以使用函数之一real、imag、abs和angle获取这些坐标。

另一方面，这种孤立的信息非常有限。例如，如果我们添加两个振幅和频率相同但相位相反的信号，则结果为零。但是，如果我们放弃相位信息，我们只是将信号加倍，这是完全错误的。

与普遍的观念相反，使用复数并不是因为这样的数字是一个方便的容器，可以容纳两个独立的值。这是因为处理周期信号始终涉及三角学，并且有一种简单的方法可以从正弦和余弦移动到更简单的复数代数：欧拉公式。

因此，大多数时候信号只是转换为其复指数形式。例如，具有10 Hz频率、3振幅和π/4弧度相位的信号：

• 可以用 x = 3.e^{i(2π.10.t+π/4)} 来描述。

• 将指数拆分：x = 3.e^i.π/4 乘以 e^i.2π.10.t，其中 t 是时间。

• 第一个数字是称为相量的常数。一个常见的简洁形式是 3∠π/4。第二个数字是随时间变化的变量，称为载波。

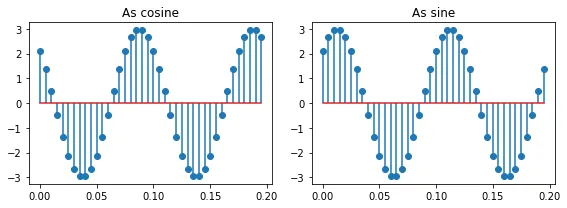
这个信号 3.e^i.π/4 times e^i.2π.10.t 可以很容易地绘制出来，可以作为余弦（实部）或正弦（虚部）：

from numpy import arange, pi, e, real, imag
t = arange(0, 0.2, 1/200)
x = 3 * e ** (1j*pi/4) * e ** (1j*2*pi*10*t)
ax1.stem(t, real(x))
ax2.stem(t, imag(x))

现在，如果我们看一下FT系数，我们会发现它们是相量，它们不嵌入频率，这只与采样数量和采样频率有关。

实际上，如果我们想在时域中绘制FT分量，我们必须单独从找到的频率创建载波，例如通过调用 fftfreq。有了相量和载波，我们就有了谱组成部分。

相量是一个向量，而向量可以旋转

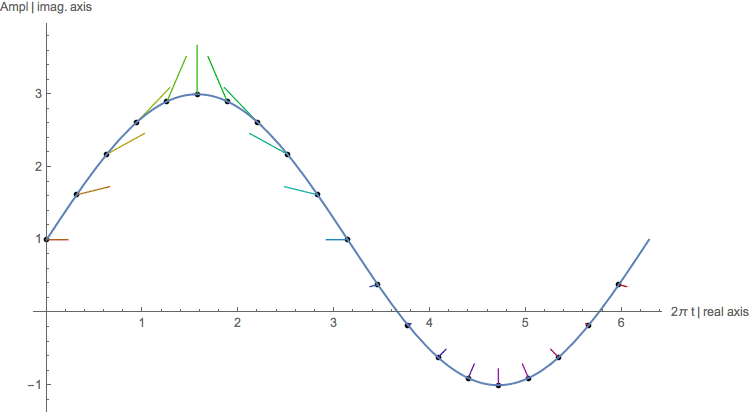
通过使用 real 和 imag 函数提取直角坐标，上面使用的相量 3.e^(i.π/4)，也是复数 2.12 + 2.12j（对于科学家和工程师来说i是j）。这些坐标可以在平面上绘制，其中垂直轴表示i（左侧）：

该点也可以表示一个向量（中心）。极坐标可以用来代替笛卡尔坐标（右图）。极坐标可以通过abs和angle提取。很明显，这个向量也可以表示为相量3∠π/4（简写形式为3.e^(i.π/4)）。

这个向量的提醒是为了介绍相量的操作方式。假设我们有一个振幅为1的实数，它不小于角度为0的复数，以及一个相量(x∠0)。我们还有第二个相量(3∠π/4)，我们想要这两个相量的乘积。我们可以使用一些三角学的笛卡尔坐标计算结果，但这很繁琐。最简单的方法是使用复指数形式：

我们只需要将角度相加并将实数系数相乘：1.e^(i.0) 乘以 3.e^(i.π/4) = 1x3.e^i(0+π/4) = 3.e^(i.π/4)。

我们可以直接写成：(1∠0) 乘以 (3∠π/4) = (3∠π/4)。

无论如何，结果就是这个：

实际效果是将实数转化并缩放其大小。在傅里叶变换中，实数是样本幅度，乘数的大小实际上为1，因此这对应于这个操作，但结果是相同的：

这个长的介绍是为了解释FT背后的数学原理。 傅里叶变换如何创建谱系数 FT的原理是，对于每个谱系数进行计算：

• 将每个样本振幅乘以不同的相位器，使得角度从第一个样本到最后一个递增，

• 求出所有先前产品的总和。

如果有N个样本x_n（0到N-1），则需要计算N个谱系数X_k。按照FT方程式计算系数X_k涉及将每个样本振幅x_n乘以相位器e^-i2πkn/N并求和。

在N个单独的产品中，乘数角度根据2π.n/N和k而变化，这意味着角度从0到2π变化，现在忽略k。因此，在执行这些产品时，我们将可变实振幅乘以一个大小为1，角度从0到完整圆的相量。我们知道这种乘法会旋转和缩放实振幅：

来源: 波恩大学物理学院的A. Dieckmann 做这个求和实际上是试图将信号样本与相量角速度相互关联，相量角速度指的是其角度随n/N变化的快慢。结果告诉我们这种关联有多强（幅度），以及它有多少同步性（相位）。

对于k个谱系数，这个操作被重复计算（一半为k负，一半为k正）。随着k的变化，角度增量也会变化，因此相互关联会针对另一个频率进行检查。

结论

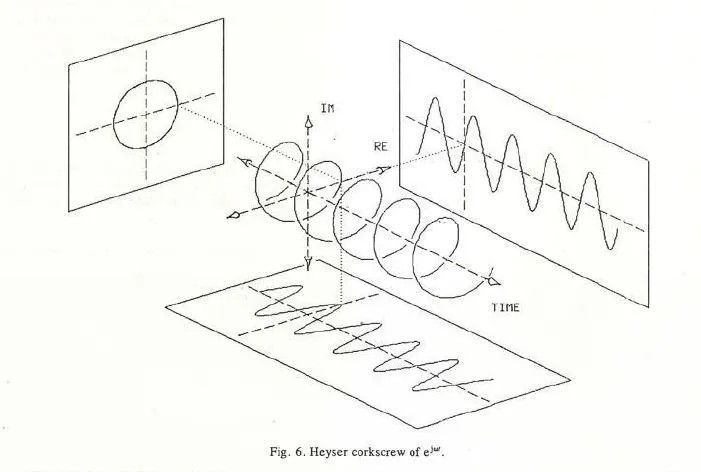
傅里叶变换的结果既不是正弦波也不是余弦波，它们是描述相关性的相量，相量是一个常量，表示为复指数，嵌入了幅度和相位。乘以载波，载波也是一个复指数，但它是可变的，取决于时间，在时域中它们绘制螺旋线。

来源

当这些螺旋体被投影到水平平面上时，通过取FT结果的实部，绘制的函数是余弦函数。当它们被投影到垂直平面上时，通过取FT结果的虚部，绘制的函数是正弦函数。相位确定了螺旋体开始的角度，因此没有相位，无法使用逆FT重建信号。

复指数乘法器是将振幅变化的线性速度转换为角速度（频率乘以2π）的工具，所有这些都围绕着欧拉公式将正弦波和复指数联系起来。

- mins

Answer 8

对于仅包含余弦波的信号，傅里叶变换(FFT)产生完全实数输出。对于仅由正弦波组成的信号，它产生完全虚数输出。任何信号中的相位偏移都将导致混合的实部和复部分。复数（在此情况下）只是存储相位和振幅的另一种方式。

- xsb