我有一条从A到B的线段,以及一个位于C处、半径为R的圆。
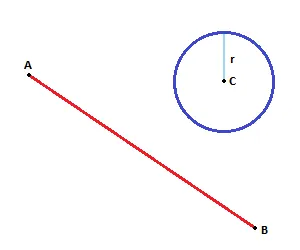
如何使用良好的算法检查该线段是否与圆相交?并且在圆的边缘上发生交点的坐标是什么?
我有一条从A到B的线段,以及一个位于C处、半径为R的圆。

如何使用良好的算法检查该线段是否与圆相交?并且在圆的边缘上发生交点的坐标是什么?
给定:
计算:
d = L - E(光线的方向向量,从开始到结束)
f = E - C(从球体中心到射线起点的向量)
然后通过以下方式找到交点..
将:
P = E + t * d
代入以下参数方程式:
Px = Ex + tdx
Py = Ey + tdy
到
(x - h)2 + (y - k)2 = r2
(h,k) = 圆的中心。
注意:这里我们简化了问题为二维,得到的解也适用于三维。
得到:
float a = d.Dot( d ) ;
float b = 2*f.Dot( d ) ;
float c = f.Dot( f ) - r*r ;
float discriminant = b*b-4*a*c;
if( discriminant < 0 )
{
// no intersection
}
else
{
// ray didn't totally miss sphere,
// so there is a solution to
// the equation.
discriminant = sqrt( discriminant );
// either solution may be on or off the ray so need to test both
// t1 is always the smaller value, because BOTH discriminant and
// a are nonnegative.
float t1 = (-b - discriminant)/(2*a);
float t2 = (-b + discriminant)/(2*a);
// 3x HIT cases:
// -o-> --|--> | | --|->
// Impale(t1 hit,t2 hit), Poke(t1 hit,t2>1), ExitWound(t1<0, t2 hit),
// 3x MISS cases:
// -> o o -> | -> |
// FallShort (t1>1,t2>1), Past (t1<0,t2<0), CompletelyInside(t1<0, t2>1)
if( t1 >= 0 && t1 <= 1 )
{
// t1 is the intersection, and it's closer than t2
// (since t1 uses -b - discriminant)
// Impale, Poke
return true ;
}
// here t1 didn't intersect so we are either started
// inside the sphere or completely past it
if( t2 >= 0 && t2 <= 1 )
{
// ExitWound
return true ;
}
// no intn: FallShort, Past, CompletelyInside
return false ;
}
t是一个数值,可以通过使用公式 P = E + t * d 中已知的其他变量和值来计算。 - Derek 朕會功夫似乎没有人考虑投影,我是不是完全错了?
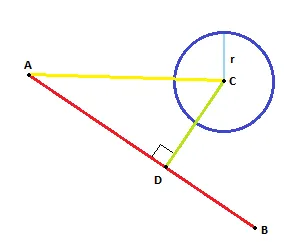
将向量AC投影到AB上。投影向量AD给出新点D。
如果D和C之间的距离小于等于R,那么它们相交。
就像这样:
对于后来找到此帖子并想知道如何实现此算法的任何人,以下是使用常见的向量操作函数编写的JavaScript通用实现。
/**
* Returns the distance from line segment AB to point C
*/
function distanceSegmentToPoint(A, B, C) {
// Compute vectors AC and AB
const AC = sub(C, A);
const AB = sub(B, A);
// Get point D by taking the projection of AC onto AB then adding the offset of A
const D = add(proj(AC, AB), A);
const AD = sub(D, A);
// D might not be on AB so calculate k of D down AB (aka solve AD = k * AB)
// We can use either component, but choose larger value to reduce the chance of dividing by zero
const k = Math.abs(AB.x) > Math.abs(AB.y) ? AD.x / AB.x : AD.y / AB.y;
// Check if D is off either end of the line segment
if (k <= 0.0) {
return Math.sqrt(hypot2(C, A));
} else if (k >= 1.0) {
return Math.sqrt(hypot2(C, B));
}
return Math.sqrt(hypot2(C, D));
}
为了实现这个功能,我使用了一些常见的向量操作函数,你可能已经在你工作环境中提供了这些函数。但是如果你还没有这些函数可用,下面是它们的实现方式。
// Define some common functions for working with vectors
const add = (a, b) => ({x: a.x + b.x, y: a.y + b.y});
const sub = (a, b) => ({x: a.x - b.x, y: a.y - b.y});
const dot = (a, b) => a.x * b.x + a.y * b.y;
const hypot2 = (a, b) => dot(sub(a, b), sub(a, b));
// Function for projecting some vector a onto b
function proj(a, b) {
const k = dot(a, b) / dot(b, b);
return {x: k * b.x, y: k * b.y};
}
(projectionPointInCircle and projectionPointOnLine) or endPointsInCircle 最后一项检查很必要,因为线段可能会穿过圆并在中心之前结束。endPoints指的是线段的起始和结束点。 - unlut// compute the euclidean distance between A and B
LAB = sqrt( (Bx-Ax)²+(By-Ay)² )
// compute the direction vector D from A to B
Dx = (Bx-Ax)/LAB
Dy = (By-Ay)/LAB
// the equation of the line AB is x = Dx*t + Ax, y = Dy*t + Ay with 0 <= t <= LAB.
// compute the distance between the points A and E, where
// E is the point of AB closest the circle center (Cx, Cy)
t = Dx*(Cx-Ax) + Dy*(Cy-Ay)
// compute the coordinates of the point E
Ex = t*Dx+Ax
Ey = t*Dy+Ay
// compute the euclidean distance between E and C
LEC = sqrt((Ex-Cx)²+(Ey-Cy)²)
// test if the line intersects the circle
if( LEC < R )
{
// compute distance from t to circle intersection point
dt = sqrt( R² - LEC²)
// compute first intersection point
Fx = (t-dt)*Dx + Ax
Fy = (t-dt)*Dy + Ay
// compute second intersection point
Gx = (t+dt)*Dx + Ax
Gy = (t+dt)*Dy + Ay
}
// else test if the line is tangent to circle
else if( LEC == R )
// tangent point to circle is E
else
// line doesn't touch circle
t+dt和t-dt处。 t是直线上最靠近圆心的点。 与圆相交的交点与t对称距离。 交点位于“距离”t-dt和t+dt处。 我引用了距离,因为它不是欧几里得距离。 要从t = 0处的A获取欧几里得距离,必须将该值乘以LAB。 - chmiket=0,点B位于t=LAB。当两个交点(t1=t-td和t2=t+td)的值都为负数时,交点在该段之外(从该点侧面望去在A点后面)。当t1和t2大于LAB时,它们也在该段之外(这次是在B点后面)。当t1(或t2)在0到LAB之间时,交点t1(或t2)仅在A和B之间发生。 - Marconius好的,我不会给你提供代码,但既然你已经打上了algorithm标签,我想这对你来说并不重要。
首先,你需要得到一条垂直于线的向量。
在 y = ax + c 方程中将会有一个未知变量 (即 c 是未知数)。
为了求解它,需要计算此线通过圆心时的值。
也就是说,
将圆心的位置代入线性方程中,并求解 c 的值。
然后计算原始线和其法线的交点。
这将给出离圆最近的线上点。
计算此点与圆心之间的距离(使用向量的大小)。
如果小于圆的半径,则表示有交点!
// compute the triangle area times 2 (area = area2/2)
area2 = abs( (Bx-Ax)*(Cy-Ay) - (Cx-Ax)(By-Ay) )
// compute the AB segment length
LAB = sqrt( (Bx-Ax)² + (By-Ay)² )
// compute the triangle height
h = area2/LAB
// if the line intersects the circle
if( h < R )
{
...
}
更新 1:
您可以通过使用快速反平方根计算方法,该方法在此处进行了描述,以获得1 / LAB的良好近似值来优化代码。
计算交点并不困难。下面是方法:
// compute the line AB direction vector components
Dx = (Bx-Ax)/LAB
Dy = (By-Ay)/LAB
// compute the distance from A toward B of closest point to C
t = Dx*(Cx-Ax) + Dy*(Cy-Ay)
// t should be equal to sqrt( (Cx-Ax)² + (Cy-Ay)² - h² )
// compute the intersection point distance from t
dt = sqrt( R² - h² )
// compute first intersection point coordinate
Ex = Ax + (t-dt)*Dx
Ey = Ay + (t-dt)*Dy
// compute second intersection point coordinate
Fx = Ax + (t+dt)*Dx
Fy = Ay + (t+dt)*Dy
vector distVector = centerPoint - projectedPoint;
if(distVector.length() < circle.radius)
{
double distance = circle.radius - distVector.length();
vector moveVector = distVector.normalize() * distance;
circle.move(moveVector);
}
http://jsfiddle.net/ercang/ornh3594/1/
如果您需要检查与线段的碰撞,还需要考虑圆心到起点和终点的距离。
vector distVector = centerPoint - startPoint;
if(distVector.length() < circle.radius)
{
double distance = circle.radius - distVector.length();
vector moveVector = distVector.normalize() * distance;
circle.move(moveVector);
}
Taking:
p1 and p2 as the points for the line, and
c as the center point for the circle and r for the radius
我会用斜率截距式解出直线的方程。但是,我不想处理带有 c 点的困难方程,所以我只是将坐标系移动到圆心为 0,0 的位置。
p3 = p1 - c
p4 = p2 - c
x值相减,再将y值相减,然后将它们放入一个新点中,以防有人不知道。p3和p4确定的直线方程:m = (p4_y - p3_y) / (p4_x - p3) (the underscore is an attempt at subscript)
y = mx + b
y - mx = b (just put in a point for x and y, and insert the m we found)
好的。现在我需要将这些方程式设为相等。首先,我需要解决圆的方程,求出x。
x^2 + y^2 = r^2
y^2 = r^2 - x^2
y = sqrt(r^2 - x^2)
然后我将它们设为相等:
mx + b = sqrt(r^2 - x^2)
解二次方程(0 = ax^2 + bx + c):
(mx + b)^2 = r^2 - x^2
(mx)^2 + 2mbx + b^2 = r^2 - x^2
0 = m^2 * x^2 + x^2 + 2mbx + b^2 - r^2
0 = (m^2 + 1) * x^2 + 2mbx + b^2 - r^2
a,b 和 c。a = m^2 + 1
b = 2mb
c = b^2 - r^2
因此,我将其代入二次公式:
(-b ± sqrt(b^2 - 4ac)) / 2a
并将值代入,然后尽可能简化:
(-2mb ± sqrt(b^2 - 4ac)) / 2a
(-2mb ± sqrt((-2mb)^2 - 4(m^2 + 1)(b^2 - r^2))) / 2(m^2 + 1)
(-2mb ± sqrt(4m^2 * b^2 - 4(m^2 * b^2 - m^2 * r^2 + b^2 - r^2))) / 2m^2 + 2
(-2mb ± sqrt(4 * (m^2 * b^2 - (m^2 * b^2 - m^2 * r^2 + b^2 - r^2))))/ 2m^2 + 2
(-2mb ± sqrt(4 * (m^2 * b^2 - m^2 * b^2 + m^2 * r^2 - b^2 + r^2)))/ 2m^2 + 2
(-2mb ± sqrt(4 * (m^2 * r^2 - b^2 + r^2)))/ 2m^2 + 2
(-2mb ± sqrt(4) * sqrt(m^2 * r^2 - b^2 + r^2))/ 2m^2 + 2
(-2mb ± 2 * sqrt(m^2 * r^2 - b^2 + r^2))/ 2m^2 + 2
(-2mb ± 2 * sqrt(m^2 * r^2 + r^2 - b^2))/ 2m^2 + 2
(-2mb ± 2 * sqrt(r^2 * (m^2 + 1) - b^2))/ 2m^2 + 2
这是它将会简化的最远程。最后,将其分离成带有±的方程式:
(-2mb + 2 * sqrt(r^2 * (m^2 + 1) - b^2))/ 2m^2 + 2 or
(-2mb - 2 * sqrt(r^2 * (m^2 + 1) - b^2))/ 2m^2 + 2
然后将这两个方程的结果直接插入到 mx + b 中的 x 变量中。为了清晰,我写了一些JavaScript代码来展示如何使用:
function interceptOnCircle(p1,p2,c,r){
//p1 is the first line point
//p2 is the second line point
//c is the circle's center
//r is the circle's radius
var p3 = {x:p1.x - c.x, y:p1.y - c.y} //shifted line points
var p4 = {x:p2.x - c.x, y:p2.y - c.y}
var m = (p4.y - p3.y) / (p4.x - p3.x); //slope of the line
var b = p3.y - m * p3.x; //y-intercept of line
var underRadical = Math.pow((Math.pow(r,2)*(Math.pow(m,2)+1)),2)-Math.pow(b,2)); //the value under the square root sign
if (underRadical < 0){
//line completely missed
return false;
} else {
var t1 = (-2*m*b+2*Math.sqrt(underRadical))/(2 * Math.pow(m,2) + 2); //one of the intercept x's
var t2 = (-2*m*b-2*Math.sqrt(underRadical))/(2 * Math.pow(m,2) + 2); //other intercept's x
var i1 = {x:t1,y:m*t1+b} //intercept point 1
var i2 = {x:t2,y:m*t2+b} //intercept point 2
return [i1,i2];
}
}
我希望这可以帮到你!
附言:如果有人发现任何错误或有任何建议,请留言。我很新,欢迎所有的帮助/建议。
underRadical 的额外 ')' - byJeevaninterceptOnCircle返回的点。类似于[i1 + c,i2 + c]以撤消第7和第8行上的转换。 - Real John Connor
// Small epsilon value
var EPS = 0.0000001;
// point (x, y)
function Point(x, y) {
this.x = x;
this.y = y;
}
// Circle with center at (x,y) and radius r
function Circle(x, y, r) {
this.x = x;
this.y = y;
this.r = r;
}
// A line segment (x1, y1), (x2, y2)
function LineSegment(x1, y1, x2, y2) {
var d = Math.sqrt( (x1-x2)*(x1-x2) + (y1-y2)*(y1-y2) );
if (d < EPS) throw 'A point is not a line segment';
this.x1 = x1; this.y1 = y1;
this.x2 = x2; this.y2 = y2;
}
// An infinite line defined as: ax + by = c
function Line(a, b, c) {
this.a = a; this.b = b; this.c = c;
// Normalize line for good measure
if (Math.abs(b) < EPS) {
c /= a; a = 1; b = 0;
} else {
a = (Math.abs(a) < EPS) ? 0 : a / b;
c /= b; b = 1;
}
}
// Given a line in standard form: ax + by = c and a circle with
// a center at (x,y) with radius r this method finds the intersection
// of the line and the circle (if any).
function circleLineIntersection(circle, line) {
var a = line.a, b = line.b, c = line.c;
var x = circle.x, y = circle.y, r = circle.r;
// Solve for the variable x with the formulas: ax + by = c (equation of line)
// and (x-X)^2 + (y-Y)^2 = r^2 (equation of circle where X,Y are known) and expand to obtain quadratic:
// (a^2 + b^2)x^2 + (2abY - 2ac + - 2b^2X)x + (b^2X^2 + b^2Y^2 - 2bcY + c^2 - b^2r^2) = 0
// Then use quadratic formula X = (-b +- sqrt(a^2 - 4ac))/2a to find the
// roots of the equation (if they exist) and this will tell us the intersection points
// In general a quadratic is written as: Ax^2 + Bx + C = 0
// (a^2 + b^2)x^2 + (2abY - 2ac + - 2b^2X)x + (b^2X^2 + b^2Y^2 - 2bcY + c^2 - b^2r^2) = 0
var A = a*a + b*b;
var B = 2*a*b*y - 2*a*c - 2*b*b*x;
var C = b*b*x*x + b*b*y*y - 2*b*c*y + c*c - b*b*r*r;
// Use quadratic formula x = (-b +- sqrt(a^2 - 4ac))/2a to find the
// roots of the equation (if they exist).
var D = B*B - 4*A*C;
var x1,y1,x2,y2;
// Handle vertical line case with b = 0
if (Math.abs(b) < EPS) {
// Line equation is ax + by = c, but b = 0, so x = c/a
x1 = c/a;
// No intersection
if (Math.abs(x-x1) > r) return [];
// Vertical line is tangent to circle
if (Math.abs((x1-r)-x) < EPS || Math.abs((x1+r)-x) < EPS)
return [new Point(x1, y)];
var dx = Math.abs(x1 - x);
var dy = Math.sqrt(r*r-dx*dx);
// Vertical line cuts through circle
return [
new Point(x1,y+dy),
new Point(x1,y-dy)
];
// Line is tangent to circle
} else if (Math.abs(D) < EPS) {
x1 = -B/(2*A);
y1 = (c - a*x1)/b;
return [new Point(x1,y1)];
// No intersection
} else if (D < 0) {
return [];
} else {
D = Math.sqrt(D);
x1 = (-B+D)/(2*A);
y1 = (c - a*x1)/b;
x2 = (-B-D)/(2*A);
y2 = (c - a*x2)/b;
return [
new Point(x1, y1),
new Point(x2, y2)
];
}
}
// Converts a line segment to a line in general form
function segmentToGeneralForm(x1,y1,x2,y2) {
var a = y1 - y2;
var b = x2 - x1;
var c = x2*y1 - x1*y2;
return new Line(a,b,c);
}
// Checks if a point 'pt' is inside the rect defined by (x1,y1), (x2,y2)
function pointInRectangle(pt,x1,y1,x2,y2) {
var x = Math.min(x1,x2), X = Math.max(x1,x2);
var y = Math.min(y1,y2), Y = Math.max(y1,y2);
return x - EPS <= pt.x && pt.x <= X + EPS &&
y - EPS <= pt.y && pt.y <= Y + EPS;
}
// Finds the intersection(s) of a line segment and a circle
function lineSegmentCircleIntersection(segment, circle) {
var x1 = segment.x1, y1 = segment.y1, x2 = segment.x2, y2 = segment.y2;
var line = segmentToGeneralForm(x1,y1,x2,y2);
var pts = circleLineIntersection(circle, line);
// No intersection
if (pts.length === 0) return [];
var pt1 = pts[0];
var includePt1 = pointInRectangle(pt1,x1,y1,x2,y2);
// Check for unique intersection
if (pts.length === 1) {
if (includePt1) return [pt1];
return [];
}
var pt2 = pts[1];
var includePt2 = pointInRectangle(pt2,x1,y1,x2,y2);
// Check for remaining intersections
if (includePt1 && includePt2) return [pt1, pt2];
if (includePt1) return [pt1];
if (includePt2) return [pt2];
return [];
}
通过将向量AC投影到向量AB上,可以在无限直线上找到距离圆心最近的点。计算该点与圆心之间的距离。如果距离大于R,则不存在交点。如果距离等于R,则直线是圆的切线,最靠近圆心的点实际上是交点。如果距离小于R,则存在2个交点。它们与最靠近圆心的点的距离相同。可以使用勾股定理轻松地计算该距离。以下是伪代码算法:
{
dX = bX - aX;
dY = bY - aY;
if ((dX == 0) && (dY == 0))
{
// A and B are the same points, no way to calculate intersection
return;
}
dl = (dX * dX + dY * dY);
t = ((cX - aX) * dX + (cY - aY) * dY) / dl;
// point on a line nearest to circle center
nearestX = aX + t * dX;
nearestY = aY + t * dY;
dist = point_dist(nearestX, nearestY, cX, cY);
if (dist == R)
{
// line segment touches circle; one intersection point
iX = nearestX;
iY = nearestY;
if (t < 0 || t > 1)
{
// intersection point is not actually within line segment
}
}
else if (dist < R)
{
// two possible intersection points
dt = sqrt(R * R - dist * dist) / sqrt(dl);
// intersection point nearest to A
t1 = t - dt;
i1X = aX + t1 * dX;
i1Y = aY + t1 * dY;
if (t1 < 0 || t1 > 1)
{
// intersection point is not actually within line segment
}
// intersection point farthest from A
t2 = t + dt;
i2X = aX + t2 * dX;
i2Y = aY + t2 * dY;
if (t2 < 0 || t2 > 1)
{
// intersection point is not actually within line segment
}
}
else
{
// no intersection
}
}
编辑:添加了代码以检查找到的交点是否在线段内。
在这个帖子中,我想补充一些内容... 以下是由pahlevan发布的代码版本,适用于C#/XNA,并进行了一些整理:
/// <summary>
/// Intersects a line and a circle.
/// </summary>
/// <param name="location">the location of the circle</param>
/// <param name="radius">the radius of the circle</param>
/// <param name="lineFrom">the starting point of the line</param>
/// <param name="lineTo">the ending point of the line</param>
/// <returns>true if the line and circle intersect each other</returns>
public static bool IntersectLineCircle(Vector2 location, float radius, Vector2 lineFrom, Vector2 lineTo)
{
float ab2, acab, h2;
Vector2 ac = location - lineFrom;
Vector2 ab = lineTo - lineFrom;
Vector2.Dot(ref ab, ref ab, out ab2);
Vector2.Dot(ref ac, ref ab, out acab);
float t = acab / ab2;
if (t < 0)
t = 0;
else if (t > 1)
t = 1;
Vector2 h = ((ab * t) + lineFrom) - location;
Vector2.Dot(ref h, ref h, out h2);
return (h2 <= (radius * radius));
}