以"银行家舍入法"指的是
根据IEEE 754 推荐：
四舍五入到最接近的值；如果数字恰好在中间，则向最接近的偶数（零）取整。这是二进制浮点数的默认舍入方式，也是十进制的推荐默认舍入方式。
据说这种方法优于
理由是它“在对舍入数求和时最小化了预期误差”。显然这是因为它在大多数合理分布下没有像远离零方法那样明显的负偏差或正偏差。
我无法理解为什么会这样。直觉上，如果将 0.0 向零取整，0.5 “应该”向远离零的方向取整（如方法2）。这样做可以使相同数量的数字向零和远离零两个方向取整。简单来说，如果浮点数用一位小数表示，在十个数字 0.0、...、0.9 中，有五个会按照方法2向下取整，还有五个会向上取整。对于 1.0、...、1.9 等情况也是类似。
当然，浮点数是用二进制底数表示的，但我认为上述推理仍然适用。请注意，对于 IEEE 754 双精度浮点数，对于绝对值最大约为 2^52 的整数和整数加半的值，都可以被精确地表示，因此这些精确值在实践中确实出现。
那么方法1为什么更好呢？
是的，使用舍入到远离零的方式确实更加数值稳定。
对于你所关注的情况，也就是数字[0.0, 0.1, ..., 0.9]，注意在采用舍入到远离零的方式时，只有其中四个数字向下舍入（从0.1到0.4），五个数字向上舍入，还有一个数字（0.0）由于舍入操作不会发生改变，然后当然这个模式会在1.0到1.9、2.0到2.9等处重复。因此，平均而言，更多的值被舍入远离零而不是靠近它。但是在采用舍入到最近偶数的方式时，我们得到了：
[0.0, 0.9]中，五个值向下舍入，四个值向上舍入[1.0, 1.9]中，四个值向下舍入，五个值向上舍入等等。平均而言，我们得到的向上舍入的数目与向下舍入的数目相同。更重要的是，在适当假设输入的分布下，由舍入引入的期望误差会更接近于零。
这里使用Python进行了快速演示。为了避免由于Python 2 / Python 3内置round函数的差异而产生困难，我们提供了两个不依赖于Python版本的四舍五入函数：
def round_ties_to_even(x):
"""
Round a float x to the nearest integer, rounding ties to even.
"""
if x < 0:
return -round_ties_to_even(-x) # use symmetry
int_part, frac_part = divmod(x, 1)
return int(int_part) + (
frac_part > 0.5
or (frac_part == 0.5 and int_part % 2.0 == 1.0))
def round_ties_away_from_zero(x):
"""
Round a float x to the nearest integer, rounding ties away from zero.
"""
if x < 0:
return -round_ties_away_from_zero(-x) # use symmetry
int_part, frac_part = divmod(x, 1)
return int(int_part) + (frac_part >= 0.5)
现在我们来看一下将这两个函数应用于小数点后一位的十进制值范围[50.0, 100.0]所引入的平均误差：
>>> test_values = [n / 10.0 for n in range(500, 1001)]
>>> errors_even = [round_ties_to_even(value) - value for value in test_values]
>>> errors_away = [round_ties_away_from_zero(value) - value for value in test_values]
我们使用最近添加的statistics标准库模块来计算这些错误的平均值和标准偏差：
>>> import statistics
>>> statistics.mean(errors_even), statistics.stdev(errors_even)
(0.0, 0.2915475947422656)
>>> statistics.mean(errors_away), statistics.stdev(errors_away)
(0.0499001996007984, 0.28723681870533313)
关键点在于errors_even的平均误差为零。但是errors_away的平均误差是有偏差的，偏离了零。
这里有一个半现实的例子，展示了数值算法中四舍五入偏移问题的偏差。我们将使用成对求和算法计算一系列浮点数的总和。该算法将要计算的总和分成两个大致相等的部分，递归地对这两部分求和，然后将结果相加。它比简单的求和方法准确得多，但通常不如更复杂的算法（如Kahan求和）好用。它是NumPy的sum函数所使用的算法。下面是一个简单的Python实现。
import operator
def pairwise_sum(xs, i, j, add=operator.add):
"""
Return the sum of floats xs[i:j] (0 <= i <= j <= len(xs)),
using pairwise summation.
"""
count = j - i
if count >= 2:
k = (i + j) // 2
return add(pairwise_sum(xs, i, k, add),
pairwise_sum(xs, k, j, add))
elif count == 1:
return xs[i]
else: # count == 0
return 0.0
我们在上述函数中添加了一个参数add，表示要使用的加法运算。默认情况下，它使用Python的标准加法算法，在典型计算机上将解析为标准IEEE 754加法，使用四舍六入模式。
我们想要查看pairwise_sum函数的预期误差，使用标准加法和使用一种从零开始的四舍五入版本的加法。我们的第一个问题是，我们没有一种简单且可移植的方法来从Python内部更改硬件的舍入模式，并且二进制浮点数的软件实现会很大且缓慢。幸运的是，有一个技巧可以在仍然使用硬件浮点的情况下获得从零开始的四舍五入。对于该技巧的第一部分，我们可以使用Knuth的“2Sum”算法来添加两个浮点数，并获得正确舍入的总和以及该总和的精确误差：
def exact_add(a, b):
"""
Add floats a and b, giving a correctly rounded sum and exact error.
Mathematically, a + b is exactly equal to sum + error.
"""
# This is Knuth's 2Sum algorithm. See section 4.3.2 of the Handbook
# of Floating-Point Arithmetic for exposition and proof.
sum = a + b
bv = sum - a
error = (a - (sum - bv)) + (b - bv)
return sum, error
有了这个，我们就可以轻松使用误差项来确定何时精确总和是平局。当且仅当error非零且sum + 2* error恰好可表示时，我们才会出现平局，在这种情况下sum和sum + 2 * error是最接近平局的两个浮点数。利用这个想法，这里是一个函数，它可以将两个数字相加并得到一个正确舍入的结果，但将平局远离零进行四舍五入。
def add_ties_away(a, b):
"""
Return the sum of a and b. Ties are rounded away from zero.
"""
sum, error = exact_add(a, b)
sum2, error2 = exact_add(sum, 2.0*error)
if error2 or not error:
# Not a tie.
return sum
else:
# Tie. Choose the larger of sum and sum2 in absolute value.
return max([sum, sum2], key=abs)
现在我们可以比较结果了。sample_sum_errors是一个函数，它生成一个范围在[1, 2]之间的浮点数列表，并使用正常的四舍六入加法和我们定制的远离零舍入模式进行相加，将其与精确的总和进行比较，并返回两个版本的误差，以最后一位单位计量。
import fractions
import random
def sample_sum_errors(sample_size=1024):
"""
Generate `sample_size` floats in the range [1.0, 2.0], sum
using both addition methods, and return the two errors in ulps.
"""
xs = [random.uniform(1.0, 2.0) for _ in range(sample_size)]
to_even_sum = pairwise_sum(xs, 0, len(xs))
to_away_sum = pairwise_sum(xs, 0, len(xs), add=add_ties_away)
# Assuming IEEE 754, each value in xs becomes an integer when
# scaled by 2**52; use this to compute an exact sum as a Fraction.
common_denominator = 2**52
exact_sum = fractions.Fraction(
sum(int(m*common_denominator) for m in xs),
common_denominator)
# Result will be in [1024, 2048]; 1 ulp in this range is 2**-44.
ulp = 2**-44
to_even_error = (fractions.Fraction(to_even_sum) - exact_sum) / ulp
to_away_error = (fractions.Fraction(to_away_sum) - exact_sum) / ulp
return to_even_error, to_away_error
这里是一个示例运行：
>>> sample_sum_errors()
(1.6015625, 9.6015625)
使用标准加法得到1.6 ulps的误差，向零舍入得到9.6 ulps的误差。似乎向零舍入方法更糟糕，但单次运行并不特别令人信服。让我们进行10000次运算，每次使用不同的随机样本，并绘制得到的误差。以下是代码：
import statistics
import numpy as np
import matplotlib.pyplot as plt
def show_error_distributions():
errors = [sample_sum_errors() for _ in range(10000)]
to_even_errors, to_away_errors = zip(*errors)
print("Errors from ties-to-even: "
"mean {:.2f} ulps, stdev {:.2f} ulps".format(
statistics.mean(to_even_errors),
statistics.stdev(to_even_errors)))
print("Errors from ties-away-from-zero: "
"mean {:.2f} ulps, stdev {:.2f} ulps".format(
statistics.mean(to_away_errors),
statistics.stdev(to_away_errors)))
ax1 = plt.subplot(2, 1, 1)
plt.hist(to_even_errors, bins=np.arange(-7, 17, 0.5))
ax2 = plt.subplot(2, 1, 2)
plt.hist(to_away_errors, bins=np.arange(-7, 17, 0.5))
ax1.set_title("Errors from ties-to-even (ulps)")
ax2.set_title("Errors from ties-away-from-zero (ulps)")
ax1.xaxis.set_visible(False)
plt.show()
Errors from ties-to-even: mean 0.00 ulps, stdev 1.81 ulps
Errors from ties-away-from-zero: mean 9.76 ulps, stdev 1.40 ulps
然后我得到了以下的图表:
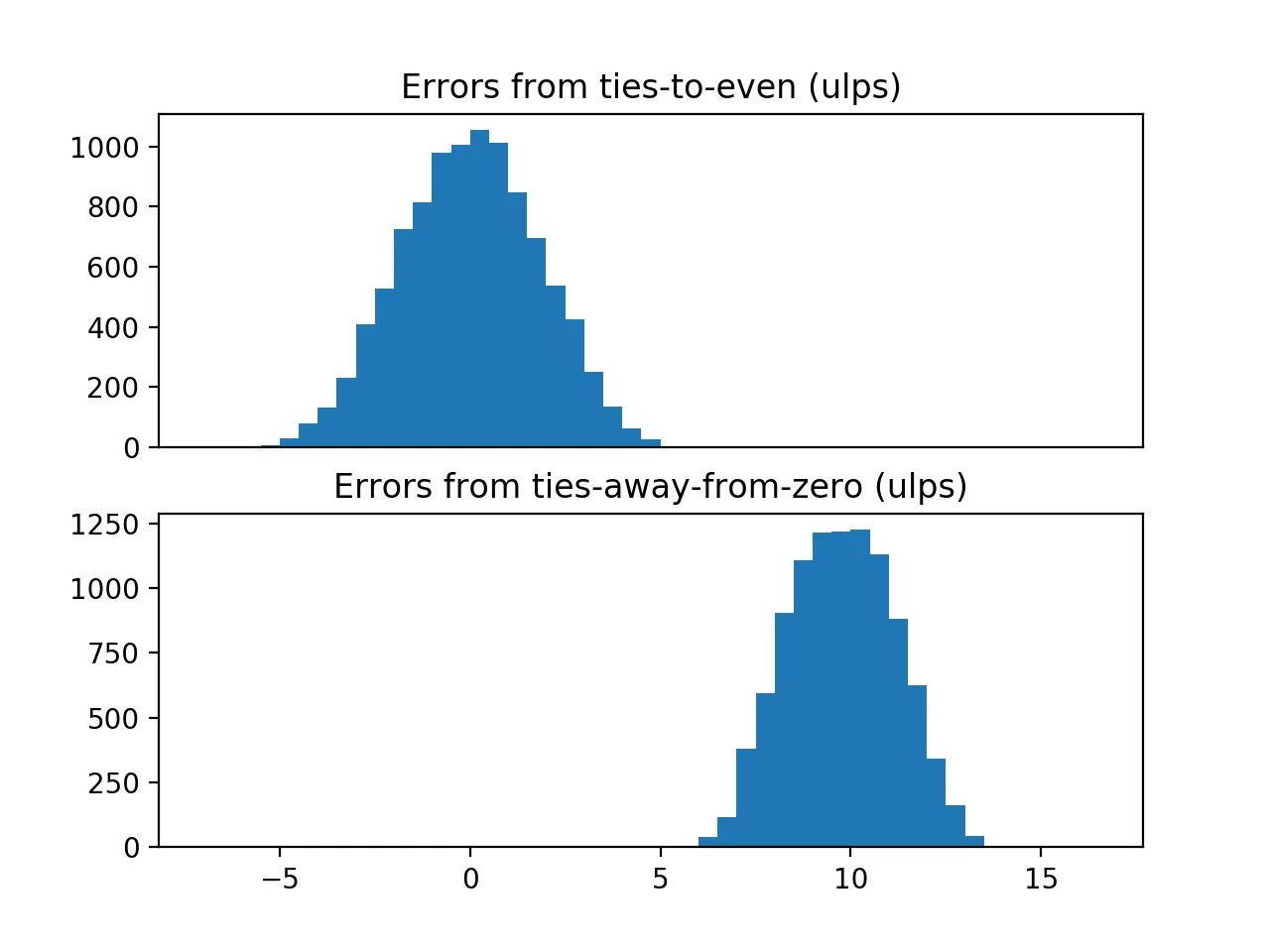
我原本计划进一步对这两个样本进行偏差的统计检验，但是ties-away-from-zero方法的偏差如此明显，以至于看起来不必要。有趣的是，虽然 ties-away-from-zero 方法给出了较差的结果，但它确实给出了更小的误差范围。
0.0еҲ°0.9зҡ„ж•°еӯ—дёӯпјҢжңүеӣӣдёӘеҗ‘дёӢиҲҚе…ҘпјҢдә”дёӘеҗ‘дёҠиҲҚе…ҘпјҢжңүдёҖдёӘдҝқжҢҒдёҚеҸҳгҖӮ - Mark Dickinson1.0开始。加上epsilon/2，减去epsilon/2，重复进行。数学上讲，无论你重复多少次，结果都应该是1.0。使用四舍五入法，你会慢慢接近2.0。 - EOF