在由0和1组成的序列中找出1的数量

Question

这是一个面试问题。一开始我觉得这很简单，有点傻。最后我没能解决它。:(

问题是，我们有一个数组，其中有一系列的0，接着是一系列的1，再接着是一系列的0，就像这样。

   int [] arr ={0,0,0,1,1,1,0,0,0}

现在，请在log(n)时间内找到数组中1的数量。

有什么想法吗？:(

- Jeevi

---

@zch，如果1的数量是恒定的，则可以在O(1)时间内获得答案。 - ikegami

不，如果您知道“1”的数量，则可以在常量时间内找到“1”的数量。具体来说，这可以在非常短的时间内完成。 - ikegami

最坏情况可能是只有一个1。我认为找到一个单独的1需要O(N)的时间复杂度。 - ikegami

我的意思是，如果您有一个或两个“1”，那么搜索肯定需要O(n)时间。一般情况下，如果他能保证至少有k个“1”，那么可以用O(n/k + lg (n-k))的时间解决，但不能更快。 - zch

很可能是一道被记错或者误解的面试问题。 - ikegami

Answer 1

嗯，该怎么说呢...

你不能。目前你只有三个关于数组的假设：

• 它不以1开头，
• 它不以1结尾，
• 对于任意两个1，它们之间没有0。

为了在数组中查找内容，您可以使用线性搜索和二进制^*搜索。线性搜索似乎不合适，因为您想要实现对数时间。然而，对于二进制搜索，您需要满足arr[i] <= arr[j]（其中i < j）。由于这种情况并不成立，您不知道哪一半包含1。这意味着您需要检查两侧，这会导致线性复杂度。

n元（n >= 2）搜索为什么不起作用

那么为什么任何类型的二进制搜索都不起作用？在回答这个问题之前，让我们快速介绍一下二进制搜索的工作原理，因为似乎有点混淆：

二进制搜索如何工作？

二进制搜索之所以如此有效，是因为它可以大大减小问题的规模：在每次迭代中，问题的规模都会减半。

例如，假设我们正在有序序列000011223334456中寻找5。

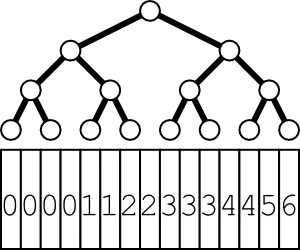
这完美地运作，因为我们得到以下序列：我们首先检查中间值，即2。因此，我们知道解决方案在右侧，我们永远不必检查左侧。右侧的中间值是四，所以我们再次切掉左半边。下一个中间值是5。我们停止：

在图像中，红色部分永远不会被检查。从复杂度的角度来看，让n成为我们最初的问题大小。经过一步之后，我们的问题大小为n/2。经过第k步，它的大小为n/(2^k)。因此，如果k = log₂ (n)，我们将问题缩小到大小为一。由于我们每步只检查了一个值，并且我们总共有log₂(n)步（向上取整），因此我们具有对数时间复杂度。

为什么二进制搜索在您的情况下不起作用

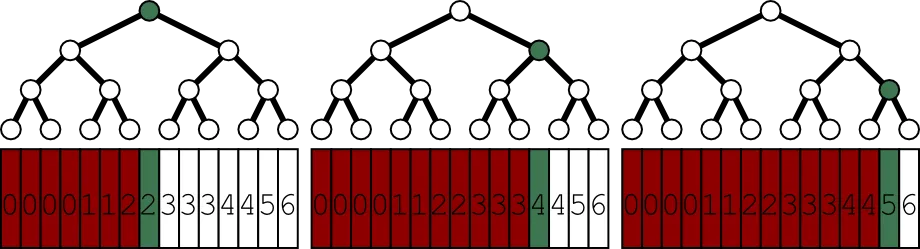
简短的答案是：因为您的问题没有排序。让我们尝试使用二进制搜索：

一个单独的步骤之后会发生什么？

检查中间值对我们来说根本没有提供任何信息，除了我们知道它不是1。我们不知道我们需要遍历左树还是右树。因此，我们需要同时遍历两者。为了创建一个确定性算法，我们需要为所有应用程序修复遍历顺序。如果我们从右到左遍历，我们会找到它相对较快：

但是如果1在左边，我们将检查几乎所有元素。您还注意到，在真实二分搜索中，我们无法排除与我们排除的节点数相同的节点。

顺便说一下，交替变体也面临着同样的问题，因为交替只意味着基于级别的遍历。您将根据它们的级别检查节点，而不是按路径跟随：

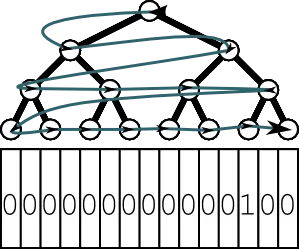
一些评论建议在两个树中进行并行/同时搜索。虽然这实际上可以减少总时间，但时间复杂度��以图灵机的思路来衡量的。在某一时刻，您会耗尽条带或CPU。请记住，这是关于理论计算时间复杂度。

为什么找到单个1如此重要？

如果您无法在对数时间内找到单个值，则无法在对数时间内找到一对值，例如（0,1）。但是如果您知道单个1的位置，则左侧和右侧是有序集，因为它们是000....011..11和11....1100...00，可以使用二分搜索。

那么人们实际上可以在对数时间内解决吗？

经过所有讨论，应该清楚我们需要线性运行时间才能找到一个单独的1。

然而，在做出假设的情况下，我们可以在对数时间内找到边缘并减去它们的位置：

• 数组在位置k处有一个1（您的示例表明size/2处有一个）

如果您想知道这有什么帮助，请查看上一节。

但是，如果没有额外的假设，则无法完成此操作。

---

^{* 或任何其他n叉搜索（n > 2），但它们都具有对数成本}

- Zeta

---

这是可能的。对两个边界进行二分查找并计算它们之间的距离。 - djechlin

@djechlin 你无法使用二分查找来寻找边界，因为你没有好的初始上/下限用于搜索。按照所呈现的问题是不可能解决的。 - interjay

@interjay 假设左侧情况，假设右侧情况，同时处理它们（即交替处理），先处理完一个。 - djechlin

@djechlin：不，这是由logc提出的，他删除了他的答案。反例：[0,0,0,...,0,1,0]。最后，你仍然遍历整个搜索树，只是不再使用常规的深度优先遍历，而是使用基于层级的遍历。你的算法的最简单反例是：[0,0,......（任意数量的零），...，0,0,0,1,0]。 - Zeta

@djechlin：另外，如果这确实是可能的，请提供一个答案。毕竟，你可能知道我不知道的东西，那个答案可能会帮助很多人 :)。 - Zeta

Answer 2

我能想到的最好解决方案：

1. 使用随机探测或随机哈希探测在数组中找到一个1
2. 从那里开始使用二分查找来找到数组中第一个和最后一个1

步骤2显然是O(log n)。问题在于步骤1是O(n/k)，其中k是数组中1的数量。如果1的数量没有任何限制，那么这就是O(n)。但是，如果要求1的数量必须是数组的某个比例（至少10%或至少1%或线性n的任何下限），则平均情况下它变成了O(1)（尽管最坏情况下仍为O(n)）。

- Chris Dodd

Answer 3

你说：

我们有一个数组，其中包含一系列0的序列，后跟一系列1的序列和一系列0的序列。

由于你的数组是以那种形式排列的，有一种方法可以在少于O(N)的时间内获取数组中1的数量。

这里有三个步骤：

1. 我们知道所有的1都在中间。在数组中找到一个包含1的索引。将该索引称为枢轴。我使用了一种没有名称的方法。以下是逻辑:

   1.1. 检查 array[N/2] 是否为1。如果是，则停止。 N/2 是枢轴。

   1.2. 检查 array[N*1/4] 和 array[N*3/4] 的值。如果其中任何一个是1，则停止。第一个找到1的索引是枢轴。

   1.3 检查 array[N*1/8]、array[N*3/8]、array[N*5/8] 和 array[N*7/8] 的值。如果其中任何一个是1，则停止。第一个找到1的索引是枢轴。

   1.4 以这种方式继续搜索，直到找到具有1的索引。

   我没有背景来确定此算法的复杂度，但我认为它比O(N)更好。

2. 我们知道1的开头必须在范围 [0:pivot] 内。使用二分法（log(N)操作）查找开始位置。将1的开始索引称为 begin。

3. 我们知道1的结尾必须在范围 [pivot+1:end-1] 内。使用二分法（log(N)操作）查找结束位置。将0在枢轴后开始的索引称为 end。

数组中1的数量为end-begin。

以下是代码的一个版本：

#include <stdio.h>
#include <iostream>
#include <algorithm>
#include <stdlib.h>
#include <time.h>
#include <assert.h>

int findBegin(int* begin, int* end, int startIndex)
{
   std::cout << "*begin: " << *begin << ", *(end-1): " << *(end-1) << ", startIndex: " << startIndex << ", distance: " << (end-begin) << std::endl;

   if ( (end - begin) < 2 )
   {
      assert(*begin == 1);
      return startIndex;
   }

   int half = (end-begin)/2;
   if ( *(begin+half-1) == 1 )
   {
      return findBegin(begin, begin+half, startIndex);
   }
   else
   {
      return findBegin(begin+half, end, startIndex+half);
   }
}

int findEnd(int* begin, int* end, int startIndex)
{
   std::cout << "*begin: " << *begin << ", *(end-1): " << *(end-1) << ", startIndex: " << startIndex << ", distance: " << (end-begin) << std::endl;

   if ( (end - begin) < 2 )
   {
      assert(*begin == 1);
      return startIndex+1;
   }

   int half = (end-begin)/2;
   if ( *(begin+half) == 0 )
   {
      return findEnd(begin, begin+half, startIndex);
   }
   else
   {
      return findEnd(begin+half, end, startIndex+half);
   }
}

int findAOne(int* begin, int startIndex, int size)
{
   int start = size/2;
   int step = size;
   while ( true )
   {
      for ( int i = start; i < size; i += step )
      {
         std::cout << "Checking for 1 at index: " << i << std::endl;
         if ( begin[i] == 1 )
         {
            return i;
         }
      }
      start = start/2;
      step = step/2;
   }

   // Should not come here unless there are no 1's in the array.
   return -1;
}

void findOnes(int array[], int N)
{
   int pivot = findAOne(array, 0, N);
   if ( pivot < 0 )
   {
      return;
   }

   std::cout << "Index where 1 is found: " << pivot << "\n\n";

   int begin = findBegin(array, array+pivot+1, 0);
   std::cout << "Done looking for begin\n\n";

   int end = findEnd(array+pivot+1, array+N, pivot);
   std::cout << "Done looking for end\n\n";

   // Print the bounds of the 1's that we found.
   std::cout << "begin of 1's found: " << begin << std::endl;
   std::cout << "end of 1's found: " << end << std::endl;
}

void fillData(int array[], int N)
{
   srand(time(NULL));
   int end1 = rand()%N;
   int end2 = rand()%N;
   int begin = std::min(end1, end2);
   int end = std::max(end1, end2);

   // Print the bounds of where the 1's are filled.
   std::cout << "begin of 1's filled: " << begin << std::endl;
   std::cout << "end of 1's filled: " << end << std::endl;

   for ( int i = 0; i != begin; ++i )
   {
      array[i] = 0;
   }

   for ( int i = begin; i != end; ++i )
   {
      array[i] = 1;
   }

   for ( int i = end; i != N; ++i )
   {
      array[i] = 0;
   }
}

int main(int argc, char** argv)
{
   int N = atoi(argv[1]);
   int* array = new int[N];

   // Fill the array with 1's in the middle.
   fillData(array, N);

   // Find the ones.
   findOnes(array, N);

   delete [] array;
}

使用1000000个点进行样本运行的输出：

1的填充开始位置：972096 1的填充结束位置：998629 在索引500000处检查1 在索引250000处检查1 在索引750000处检查1 在索引125000处检查1 在索引375000处检查1 在索引625000处检查1 在索引875000处检查1 在索引62500处检查1 在索引187500处检查1 在索引312500处检查1 在索引437500处检查1 在索引562500处检查1 在索引687500处检查1 在索引812500处检查1 在索引937500处检查1 在索引31250处检查1 在索引93750处检查1 在索引156250处检查1 在索引218750处检查1 在索引281250处检查1 在索引343750处检查1 在索引406250处检查1 在索引468750处检查1 在索引531250处检查1 在索引593750处检查1 在索引656250处检查1 在索引718750处检查1 在索引781250处检查1 在索引843750处检查1 在索引906250处检查1 在索引968750处检查1 在索引15625处检查1 在索引46875处检查1 在索引78125处检查1 在索引109375处检查1 在索引140625处检查1 在索引171875处检查1 在索引203125处检查1 在索引234375处检查1 在索引265625处检查1 在索引296875处检查1 在索引328125处检查1 在索引359375处检查1 在索引390625处检查1 在索引421875处检查1 在索引453125处检查1 在索引484375处检查1 在索引515625处检查1 在索引546875处检查1 在索引578125处检查1 在索引609375处检查1 在索引640625处检查1 在索引671875处检查1 在索引703125处检查1 在索引734375处检查1 在索引765625处检查1 在索引796875处检查1 在索引828125处检查1 在索引859375处检查1 在索引890625处检查1 在索引921875处检查1 在索引953125处检查1 在索引984375处检查1 找到1的索引位置：984375

*开始：0，*(结束-1)：1，起始索引：0，距离：984376 *开始：0，*(结束-1)：1，起始索引：492188，距离：492188 *开始：0，*(结束-1)：1，起始索引：738282，距离：246094 *开始：0，*(结束-1)：1，起始索引：861329，距离：123047 *开始：0，*(结束-1)：1，起始索引：922852，距离：61524 *开始：0，*(结束-1)：1，起始索引：953614，距离：30762 *开始：0，*(结束-1)：1，起始索引：968995，距离：15381 *开始：0，*(结束-1)：1，起始索引：968995，距离：7690 *开始：0，*(结束-1)：1，起始索引：968995，距离：3845 *开始：0，*(结束-1)：1，起始索引：970917，距离：1923 *开始：0，*(结束-1)：1，起始索引：971878，距离：962 *开始：0，*(结束-1)：1，起始索引：971878

从输出可以看出，寻找枢轴需要65步。在找到枢轴后，寻找begin和end非常快。

- R Sahu

---

“我认为它比O(N)更好。” 不是的，它是O(N)。你可以轻松构建一个数组，在这个数组中你会查看几乎所有的元素：arr[2^n] = [0,0,0,0,0,0,0,0,...,0,1,0,0]。请参考我的答案，查看你提出的遍历方式的图像。它是基于层级/广度优先的。 - Zeta

@Zeta，感谢您的解释。我明白为什么最坏情况下是O（N）操作。最好情况下是常数时间操作。我不知道如何表述查找1的平均成本。 - R Sahu

Answer 4

证明复杂度不是O(log n)的一种方法是找到一个复杂度为O(n)的示例。

考虑一个仅包含一个1的数组。计算1的数量的问题将等同于定位那个单独的1的问题。当探测数组时，除了知道它是1还是0之外，我们不会得到任何额外的信息。我们不知道在1之前或之后进行了探测。这意味着为了保证我们找到1，我们必须对数组进行n次探测，即O(n)。

因此，不是O(log n)。

- Martin G