Big O混淆：log2(N) vs log3(N)

Question

为什么O(log₂N) = O(log₃N) ?

我不太理解这点。难道大O符号不意味着某个东西的上界吗？

log₂N不比log₃N 大吗？当我绘制它们的图形时，log₂N在log₃N上方。

- Daver Muzaffar

---

提示：尝试转换为3进制，并记住常数并不重要。 - msgambel

你也可以使用极限来帮助找到答案。lim_{x->infty}(log_2n/log_3n) = ln3/ln2 = 约为1.58。 - J'e

Answer 1

Big O并不涉及常数因子，而Log_x(n)和Log_y(n)之间的区别只是一个常数因子。

换个说法，对数的底数基本上只修改了图表上线条/曲线的斜率。Big-O并不关心图表上曲线的斜率，只关心曲线的形状。如果你可以通过将其斜率向上或向下移动使一条曲线匹配另一条曲线，那么就在Big-O符号意义上它们是相同的函数和相同的曲线。

为了更好地理解，也许绘制一些常见曲线形状的图会有用：

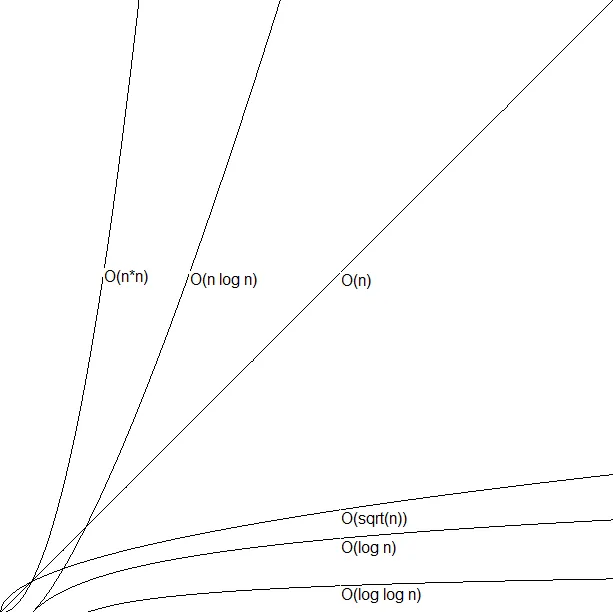
如上所述，只有线的形状才重要，而不是它的斜率。在以下图中：

...所有线都是直线，因此即使它们的斜率差异激增，它们在大O符号意义上仍然相同--它们都只是O(N)，无论斜率如何。对于对数来说，我们得到了大致相同的效果--每条线都会像前面图片中的O(log N)线一样弯曲，但是更改对数的底数将使该曲线绕原点旋转，因此你将（再次）获得相同的形状，但是斜率不同（因此，从大O符号意义上来看，它们都是相同的）。因此，回到最初的问题，如果我们更改对数的底数，我们将得到类似以下图表的曲线：

在这里，可能不太明显的是发生的只是斜率不断地变化，但这正是与上面的直线相同的区别。

- Jerry Coffin

---

我还要指出的是，不仅仅是移位不重要，我们也忽略常数的乘法。无论 f = n 还是 f = 2n，f 都是 O(n)，即使 2n 不是 n 的向上移位。事实上，我认为忽略常数因素是大 O 表示法更重要的特征。 - Sean

Answer 2

这是因为更改对数的底数相当于将其乘以一个常数。而大O符号并不关心常数。

log_a(b) = log_c(b) / log_c(a)

因此，要从log2(n)转换为log3(n)，您需要将其乘以1 / log(3) 2。

换句话说， log2(n) = log3(n) / log3(2)。

log3(2)是一个常数，O(cn) = O(n)，因此O(log2(n)) = O(log3(n))。

- luk32

Answer 3

这里已经有一些好的答案了，请也阅读它们。要理解为什么Log2(n)是O(log3(n))，您需要了解两件事情。

1）什么是大O符号。我建议阅读这篇文章：http://en.wikipedia.org/wiki/Big_O_notation 如果您理解了这个，您就会知道2n和16n+5都是O(N)。

2）对数是如何工作的。log₂(N)和log₁₀(N)之间的区别将是一个简单的比率，如果您想按照luk32的答案计算，可以轻松地进行计算。

由于不同基数的对数仅相差一个常量比率，并且大O符号对于像常量乘法因子这样的小事情是无关紧要的，因此您经常会发现O(logN)实际上省略了底数，因为在这种情况下选择任何常数底数（例如2、3、10、e）都没有影响。

- RichardPlunkett

Answer 4

这取决于使用O符号的上下文。当您在算法复杂性推理中使用它时，您对函数的渐近行为感兴趣，即当函数趋于（正或负）无穷大（或另一个积累点）时它如何增长/减少。

因此，尽管f(n)=3n始终小于g(n)=1000n，但它们都出现在O(n)中，因为它们根据它们的表达式渐近地增长线性。

对于您发布的对数情况，可以采用相同的推理方法，因为不同基数的对数之间存在一个常数因子差异，但它们共享相同的渐近行为。

如果您有兴趣计算算法的确切性能，并且您的估计是精确而不是近似的，则当然更喜欢较低的那个。通常，所有计算复杂度比较都是通过渐近推理进行的，因此都是近似的。

- rano