计算递归关系式 T(n) = sqrt(n * T(sqrt(n)) + n)。

Question

我认为通过变量替换和归纳，这种递归的复杂度是O(n^2/3)。但我不确定。这个解决方案是否正确？

- erfan30

Answer 1

这是一个有趣的循环，但它并不解决Θ(n)。相反，似乎解决为Θ(n^2/3)。为了说明为什么这不可能是Θ(n)，让我们想象我们正在处理一个非常大的n值。那么，由于假设T(√n) ≈ √n，我们得到T(n) = (n√n + n)^1/2，即T(n)≈n^3/4。换句话说，假设T(n) = Θ(n)将在n变大时给我们不同的T(n)值。另一方面，假设T(n) = Θ(n^2/3)，则相同的计算给出T(n)≈n^3/4。

T(n) = (nT(n) + n)^1/2

= (n · n^2/3 + n)^1/2

≈ (n^4/3)^1/2

= n^2/3,

这与自身一致。

为了验证这一点，我编写了一个简短的程序，给出不同输入值的 T(n) 值并绘制结果。以下是我编写的 T(n) 版本：

double T(double n) {
  if (n <= 2) return n;
  return sqrt(n * T(sqrt(n)) + n);
}

我决定以2作为基本情况，因为反复取平方根永远不会让n降到1。我还决定使用实值参数而不是离散整数值，只是为了使数学更容易。

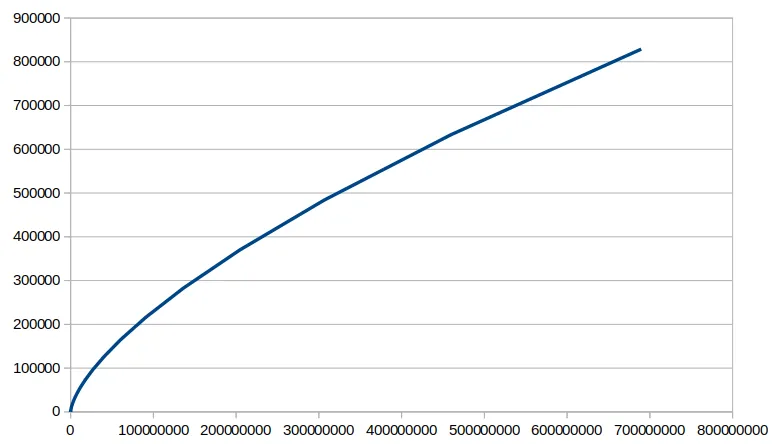
如果你绘制T(n)的值，你会得到这条曲线：

.

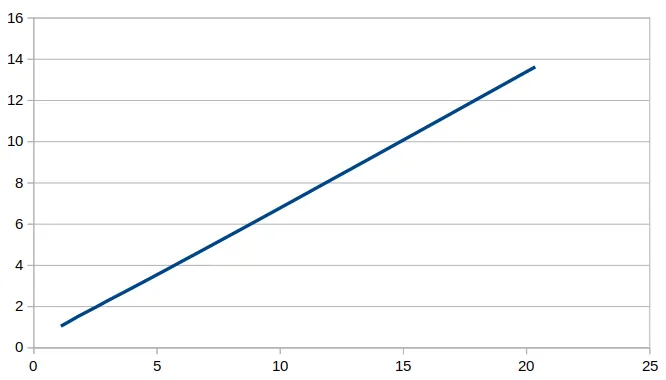
这看起来不像是线性图。为了弄清楚这是什么，我在对数/对数图上绘制了它，这个图具有很好的特性，即所有多项式函数都被转换为斜率等于指数的直线。以下是结果：

我使用了便利的邻域回归软件，并要求它确定这条线的斜率。以下是它给出的结果：

坡度：0.653170918815869 R²：0.999942627574643

这是一个非常好的拟合，斜率为0.653，非常接近2/3。因此，这是更多支持递归解为Θ(n^2/3)的经验证据。

现在只剩下数学问题需要解决了。我们将使用一系列替换来解决这个递归式。

首先，我通常不太喜欢按照递归式中所使用的方式处理指数，因此让我们对两边取对数。（在本文中，我将使用lg n表示log2 n）。

lg T(n) = lg (nT(√n) + n)^1/2

= (1/2) lg (nT(√n) + n)

= (1/2) lg(T(√n) + 1) + (1/2)lg n

≈ (1/2) lg T(√n) + (1/2) lg n

现在，让我们定义 S(n) = lg T(n)，那么我们有：

S(n) = lg T(n)

≈ (1/2) lg T(√ n) + (1/2) lg n

= (1/2) S(√ n) + (1/2) lg n

这样就容易处理多了，但是我们仍然面临着每次递归都会缩小幂次的问题。为了解决这个问题，让我们再做一个替换，这在处理这种表达式时是相当常见的。让我们定义 R(n) = S(2ⁿ)。那么我们有：

R(n) = S(2ⁿ)

≈ (1/2)S(√2ⁿ) + (1/2) lg 2ⁿ

= (1/2)S(2^n/2) + (1/2) n

= (1/2) R(n / 2) + (1/2) n

太好了！现在只需要解决R(n)。

现在有一个小问题。我们可以立即使用主定理得出R(n) = Θ(n)。但是，仅知道R(n) = Θ(n)并不能确定T(n)是什么。具体来说，假设我们只知道R(n) = Θ(n)，那么我们可以说

S(n) = S(2^{lg n}) = R(lg n) = Θ(log n)

以得到S(n) = Θ(log n)。然而，在尝试用S(n)求解T(n)时，我们卡住了。具体来说，我们知道

T(n) = 2的S(n)次方 = 2的Θ(log n)次方， 但我们不能从中得出T(n) = Θ(n)的结论。原因是Θ(log n)中隐藏的系数在这里是重要的。具体来说，如果S(n) = k lg n，则有 2的k lg n次方 = 2的lg n的k次方 = n的k次方， 因此对数的主导系数最终将确定多项式的指数。因此，在解决R时，我们需要确定线性项的确切系数，这转化为S的对数项的确切系数。 因此，让我们回到我们所知道的R(n)，即 R(n) ≈ (1/2) R(n/2) + (1/2)n。 如果我们迭代几次，我们会看到这个模式：

R(n) ≈ (1/2) R(n/2) + (1/2)n

≈ (1/2)((1/2) R(n/4) + (1/4)n) + (1/2)n

≈ (1/4)R(n/4) + (1/8)n + (1/2)n

≈ (1/4)((1/2)R(n/8) + n/8) + (1/8)n + (1/2)n

≈ (1/8)R(n/8) + (1/32)n + (1/8)n + (1/2)n.

模式是，在 k 次迭代后，我们得到：

R(n) ≈ (1/2^k)R(n/2^k) + n(1/2 + 1/8 + 1/32 + 1/128 + ... + 1/2^2k+1)。

这意味着我们应该看一下这个求和：

(1/2) + (1/8) + (1/32) + (1/128) + ...

这是

(1/2)(1 + 1/4 + 1/16 + 1/64 + ... )

它作为一个等比数列的和，解出来是

(1/2)(4/3)

= 2/3.

看！这就是我们之前说的2/3。这意味着R(n)大约为(2/3)n + c，其中c是取决于递归基的常数。因此，我们可以得出

= 2的S(2的lg n次方)次方

= 2的R(lg n)次方

≈ 2的(2/3)lg n + c次方

= 2的lg n的2/3次方 + c次方

= 2的c次方 * n的2/3次方

= Θ(n的2/3次方)

这与之前理论预测和实际观察到的值相符。

解决这个问题非常有趣，我承认答案让我感到惊讶！不过，当我从

lg T(n) = (1/2) lg (T(√n) + 1) + (1/2) lg n

转化为上面的式子时，我有点紧张，担心可能漏掉了什么。

lg T(n) ≈ (1/2) lg T(√ n) + (1/2) lg n.

可能会出现一个+1的项，实际上会在递归中引入一些我没有意识到的其他项。例如，是否会出现一个O(log log n)的项？这并不奇怪，因为我们有一个按平方根缩小的递归。但是，我进行了一些简单的数据探索，没有看到任何看起来涉及双对数的项。

希望这可以帮助您！

- templatetypedef

Answer 2

我们知道：

T(n) = sqrt(n) * sqrt(T(sqrt(n)) + 1)

因此：

T(n) < sqrt(n) * sqrt(T(sqrt(n)) + T(sqrt(n)))

1 被 T(sqrt(n)) 替换。因此，

T(n) < sqrt(2) * sqrt(n) * sqrt(T(sqrt(n))

现在，为了找到一个上界，我们需要解决以下递归关系：

G(n) = sqrt(2n) * sqrt(G(sqrt(n))

为了解决这个问题，需要进行扩展（假设 n = 2^{2^k} 并且 T(1) = 1）：

G(n) = (2n)^{1/2} * (2n)^{1/8} * (2n)^{1/32} * ... * (2n)^(1/2^k) => 
G(n) = (2n)^{1/2 + 1/8 + 1/32 + ... + 1/2^k} = 

如果我们从 1/2 + 1/8 + 1/32 + ... + 1/2^k 中取出因子1/2，我们将得到 1/2 * (1 + 1/4 + 1/8 + ... + 1/2^{k-1})。 正如我们所知道的，1 + 1/4 + 1/8 + ... + 1/2^{k-1} 是一个公比为1/4的等比数列，在无穷大时它等于 4/3。因此，G(n) = Theta(n^{2/3}) 并且 T(n) = O(n^{2/3})。

注意，因为 sqrt(n) * sqrt(T(sqrt(n)) < T(n)，我们可以像前面的情况一样表明 T(n) = Omega(n^{2/3})。这意味着 T(n) = Theta(n^{2/3})。

- OmG

---

我认为你在这里可能有一个小但重要的数学错误。具体来说，在迭代递归时，我认为你将其中一个平方根（T(sqrt(n))中的那个）因式分解了，但没有将另一个（外部sqrt(n)）因式分解。这会导致你所拥有的几何级数以1/2 + 1/8 + 1/32 + 1/128 + ...的速度衰减，其总和为2/3而不是1。我进行了一些实验，似乎n^{2/3}才是正确的答案，而不是n。 - templatetypedef

@templatetypedef 好的，感谢您的评论。 - OmG