我有一个高度为整数且宽度恒定为1的直方图。我想最大化直方图下面的矩形区域。 例如：
_
| |
| |_
| |
| |_
| |
答案是6，即使用col1和col2相乘得到。
我知道O(n^2)的暴力方法，但我想要一个O(n log n)的算法。我尝试考虑最大递增子序列的动态规划算法（O(n log n)），但是卡住了。我应该使用分治算法吗？
PS：有足够声望的人请删除divide-and-conquer标签，如果没有这样的解决方案。
mho的评论之后：我的意思是适合完全适配的最大矩形区域。（感谢j_random_hacker澄清 :)）。
while x < stack.top():
stack.pop()
stack.push(x)
stack[x]，stack[x-1]是其左侧第一个更小的元素，然后一个可以弹出stack[x]的新元素是其右侧第一个更小的元素。
你还不相信 stack[x-1] 是在 stack[x] 左侧第一个更小的元素吗？
我将通过反证法来证明。
首先，stack[x-1] < stack[x] 当然是成立的。但是假设 stack[x-1] 不是 stack[x] 左侧的第一个更小的元素。
那么第一个更小的元素 fs 在哪里呢？
If fs < stack[x-1]:
stack[x-1] will be popped out by fs,
else fs >= stack[x-1]:
fs shall be pushed into stack,
Either case will result fs lie between stack[x-1] and stack[x], which is contradicting to the fact that there is no item between stack[x-1] and stack[x].
def largestRectangleArea(A):
ans = 0
A = [-1] + A
A.append(-1)
n = len(A)
stack = [0] # store index
for i in range(n):
while A[i] < A[stack[-1]]:
h = A[stack.pop()]
area = h*(i-stack[-1]-1)
ans = max(ans, area)
stack.append(i)
return ans
(x, height[x])仍然是您可以获得的最大区域为5。 - yangmillstheorypublic int solution1(int[] height) {
int n = height.length;
if(n == 0) return 0;
int[][] dp = new int[n][n];
int max = Integer.MIN_VALUE;
for(int width = 1; width <= n; width++){
for(int l = 0; l+width-1 < n; l++){
int r = l + width - 1;
if(width == 1){
dp[l][l] = height[l];
max = Math.max(max, dp[l][l]);
} else {
dp[l][r] = Math.min(dp[l][r-1], height[r]);
max = Math.max(max, dp[l][r] * width);
}
}
}
return max;
}
public int Solution2(int[] height) {
int n = height.length;
if(n == 0) return 0;
int max = Integer.MIN_VALUE;
// dp[0] and dp[1] take turns to be the "previous" line.
int[][] dp = new int[2][n];
for(int width = 1; width <= n; width++){
for(int l = 0; l+width-1 < n; l++){
if(width == 1){
dp[width%2][l] = height[l];
} else {
dp[width%2][l] = Math.min(dp[1-width%2][l], height[l+width-1]);
}
max = Math.max(max, dp[width%2][l] * width);
}
}
return max;
}
For each bar, we must be able to find the biggest rectangle containing this bar. So the biggest one of these n rectangles is what we want.
To get the biggest rectangle for a certain bar (let's say bar[i], the (i+1)th bar), we just need to find out the biggest interval that contains this bar. What we know is that all the bars in this interval must be at least the same height with bar[i]. So if we figure out how many consecutive same-height-or-higher bars are there on the immediate left of bar[i], and how many consecutive same-height-or-higher bars are there on the immediate right of the bar[i], we will know the length of the interval, which is the width of the biggest rectangle for bar[i].
To count the number of consecutive same-height-or-higher bars on the immediate left of bar[i], we only need to find the closest bar on the left that is shorter than the bar[i], because all the bars between this bar and bar[i] will be consecutive same-height-or-higher bars.
We use a stack to dynamicly keep track of all the left bars that are shorter than a certain bar. In other words, if we iterate from the first bar to bar[i], when we just arrive at the bar[i] and haven't updated the stack, the stack should store all the bars that are no higher than bar[i-1], including bar[i-1] itself. We compare bar[i]'s height with every bar in the stack until we find one that is shorter than bar[i], which is the cloest shorter bar. If the bar[i] is higher than all the bars in the stack, it means all bars on the left of bar[i] are higher than bar[i].
We can do the same thing on the right side of the i-th bar. Then we know for bar[i] how many bars are there in the interval.
public int solution3(int[] height) {
int n = height.length;
if(n == 0) return 0;
Stack<Integer> left = new Stack<Integer>();
Stack<Integer> right = new Stack<Integer>();
int[] width = new int[n];// widths of intervals.
Arrays.fill(width, 1);// all intervals should at least be 1 unit wide.
for(int i = 0; i < n; i++){
// count # of consecutive higher bars on the left of the (i+1)th bar
while(!left.isEmpty() && height[i] <= height[left.peek()]){
// while there are bars stored in the stack, we check the bar on the top of the stack.
left.pop();
}
if(left.isEmpty()){
// all elements on the left are larger than height[i].
width[i] += i;
} else {
// bar[left.peek()] is the closest shorter bar.
width[i] += i - left.peek() - 1;
}
left.push(i);
}
for (int i = n-1; i >=0; i--) {
while(!right.isEmpty() && height[i] <= height[right.peek()]){
right.pop();
}
if(right.isEmpty()){
// all elements to the right are larger than height[i]
width[i] += n - 1 - i;
} else {
width[i] += right.peek() - i - 1;
}
right.push(i);
}
int max = Integer.MIN_VALUE;
for(int i = 0; i < n; i++){
// find the maximum value of all rectangle areas.
max = Math.max(max, width[i] * height[i]);
}
return max;
}
Python实现@IVlad的答案 O(n)解决方案：
from collections import namedtuple
Info = namedtuple('Info', 'start height')
def max_rectangle_area(histogram):
"""Find the area of the largest rectangle that fits entirely under
the histogram.
"""
stack = []
top = lambda: stack[-1]
max_area = 0
pos = 0 # current position in the histogram
for pos, height in enumerate(histogram):
start = pos # position where rectangle starts
while True:
if not stack or height > top().height:
stack.append(Info(start, height)) # push
elif stack and height < top().height:
max_area = max(max_area, top().height*(pos-top().start))
start, _ = stack.pop()
continue
break # height == top().height goes here
pos += 1
for start, height in stack:
max_area = max(max_area, height*(pos-start))
return max_area
例子：
>>> f = max_rectangle_area
>>> f([5,3,1])
6
>>> f([1,3,5])
6
>>> f([3,1,5])
5
>>> f([4,8,3,2,0])
9
>>> f([4,8,3,1,1,0])
9
复制粘贴算法描述（以防页面崩溃）：
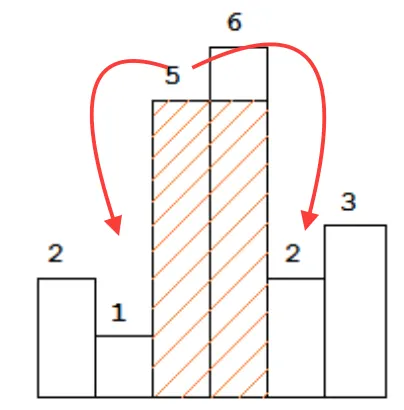
我们按照从左到右的顺序处理元素，并维护有关已开始但尚未完成的子直方图的信息堆栈。每当出现新元素时，它都会遵循以下规则。如果堆栈为空，我们通过将元素推入堆栈来打开新的子问题。否则，我们将其与堆栈顶部的元素进行比较。如果新元素更大，我们再次将其推入堆栈。如果新元素相等，则跳过它。在所有这些情况下，我们继续处理下一个新元素。如果新元素更小，则通过更新堆栈顶部元素的最大区域来完成最高的子问题。然后，我们丢弃顶部的元素，并重复该过程以保留当前新元素。这样，所有子问题都会完成，直到堆栈变为空，或其顶部元素小于或等于新元素，从而导致上述操作。如果已处理所有元素并且堆栈尚未为空，则通过更新与顶部元素相关的最大区域来完成剩余的子问题。start属性）。当堆栈弹出时，结束位置是直方图中的当前位置（pos变量），请参见height < top().height分支。 - jfs其他答案已经很好地介绍了使用两个堆栈的O(n)时间复杂度、O(n)空间复杂度的解决方案。对于这个问题，还有另一个角度提供了独立的O(n)时间复杂度、O(n)空间复杂度的解决方案，并且可能会更深入地解释为什么基于堆栈的解决方案有效。
关键思想是使用一种数据结构称为笛卡尔树。笛卡尔树是一种二叉树结构（虽然不是二叉搜索树），围绕输入数组构建而成。具体来说，笛卡尔树的根建立在数组的最小元素上，左右子树从最小值的左侧和右侧的子数组递归构建。
例如，这里有一个示例数组及其笛卡尔树：
+----------------------- 23 ------+
| |
+------------- 26 --+ +-- 79
| | |
31 --+ 53 --+ 84
| |
41 --+ 58 -------+
| |
59 +-- 93
|
97
+----+----+----+----+----+----+----+----+----+----+----+
| 31 | 41 | 59 | 26 | 53 | 58 | 97 | 93 | 23 | 84 | 79 |
+----+----+----+----+----+----+----+----+----+----+----+
笛卡尔树在这个问题中很有用的原因是，所提出的问题具有非常好的递归结构。首先看一下直方图中最低的矩形。对于最大矩形可能出现的位置，有三种情况：
它可能经过直方图中的最小值。在这种情况下，为了使其尽可能大，我们希望将其宽度设为整个数组的宽度。
它可能完全位于最小值左侧。在这种情况下，我们需要递归地处理最小值左侧的子数组以得到答案。
它可能完全位于最小值右侧。在这种情况下，我们需要递归地处理最小值右侧的子数组以得到答案。
注意，这种递归结构-找到最小值，在最小值左右的子数组中进行某些操作-与笛卡尔树的递归结构完全匹配。事实上，如果我们在开始时可以为整个数组创建一个笛卡尔树，则可以通过从根向下递归遍历笛卡尔树来解决此问题。在每个节点处，我们递归计算左右子数组中的最佳矩形，以及通过放置在最小值下方所得到的矩形，然后返回找到的最佳选项。
伪代码如下：
function largestRectangleUnder(int low, int high, Node root) {
/* Base case: If the range is empty, the biggest rectangle we
* can fit is the empty rectangle.
*/
if (low == high) return 0;
/* Assume the Cartesian tree nodes are annotated with their
* positions in the original array.
*/
return max {
(high - low) * root.value, // Widest rectangle under the minimum
largestRectangleUnder(low, root.index, root.left),
largestRectnagleUnder(root.index + 1, high, root.right)
}
}
一旦我们获得Cartesian树，此算法的时间复杂度为O(n)，因为我们恰好访问每个节点并且每个节点只需进行O(1)次操作。
事实证明，有一种简单的线性时间算法可用于构建Cartesian树。您可能会想到“自然”的构建方法是扫描数组，找到最小值，然后递归地从左右子数组构建Cartesian树。问题在于查找最小值的过程非常昂贵，这可能需要Θ(n²)的时间。
构建Cartesian树的“快速”方法是从左到右扫描数组，逐个添加一个元素。该算法基于以下关于Cartesian树的观察结果:
首先，Cartesian树遵循堆属性：每个元素都小于或等于其子元素。原因在于，Cartesian树根是整个数组中最小的值，而其子元素是它们自己子数组中的最小元素，以此类推。
其次，如果对Cartesian树进行中序遍历，则可以按它们出现的顺序返回数组的元素。要了解为什么，请注意，如果对Cartesian树进行中序遍历，则首先访问最小值左侧的所有内容，然后是最小值，最后是最小值右侧的所有内容。这些访问以相同的方式递归进行，因此每个元素最终都按顺序被访问。
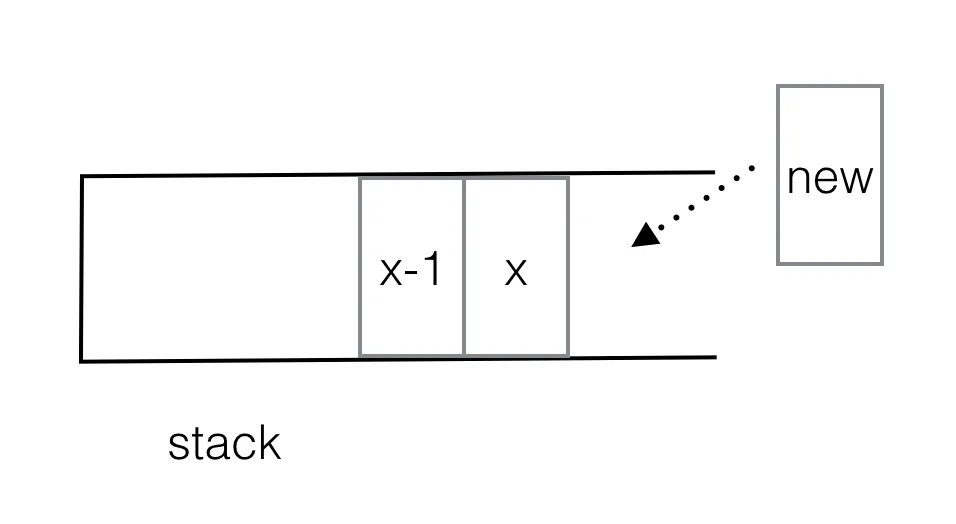
这两条规则为我们提供了有关从数组的前k个元素开始构建Cartesian树并且想要形成前k + 1个元素的Cartesian树时会发生什么的许多信息。该新元素将必须出现在Cartesian树的右脊柱上 - 即从根节点开始向右移动的部分 - 因为否则中序遍历中会有其它元素紧随其后。而且，在该右脊柱内，它必须以使其大于其上面的所有元素的方式放置，因为我们需要遵守堆属性。
实际上添加新节点到Cartesian树的方法是从树中最右侧的节点开始向上遍历，直到到达树的根节点或者找到具有更小值的节点。然后，将新值的左子节点设置为在其上方最后遍历的节点。
下面是在一个小数组上应用该算法的示例：
+---+---+---+---+
| 2 | 4 | 3 | 1 |
+---+---+---+---+
2成为根节点。
2 --+
|
4
4比2大，我们不能向上移动。追加到右侧。
+---+---+---+---+
| 2 | 4 | 3 | 1 |
+---+---+---+---+
2 ------+
|
--- 3
|
4
3小于4，爬过它。 无法继续超过2，因为它比3小。 爬过以4为根的子树将移动到新值3的左侧，现在3成为最右边的节点。
+---+---+---+---+
| 2 | 4 | 3 | 1 |
+---+---+---+---+
+---------- 1
|
2 ------+
|
--- 3
|
4
1爬过根节点2后，以2作为根的整个树被移动到1的左侧，1现在成为新的根，同时也是最右侧的值。
+---+---+---+---+
| 2 | 4 | 3 | 1 |
+---+---+---+---+
现在关键的一步——实际实现这种方法的标准方式是通过维护一个对应于右侧脊柱上节点的值的堆栈来完成的。沿着节点“向上”和跨越节点相当于弹出堆栈中的一个元素。因此，构建笛卡尔树的代码看起来像这样：
Stack s;
for (each array element x) {
pop s until it's empty or s.top > x
push x onto the stack.
do some sort of pointer rewiring based on what you just did.
}
这里的堆栈操作可能会很熟悉，因为这些操作与其他答案中显示的完全相同。实际上，你可以将那些方法看作是在隐式构建笛卡尔树以及在此过程中运行上面显示的递归算法。
我认为了解笛卡尔树的好处在于它提供了一个非常好的概念框架，可以看到为什么该算法能正确地工作。如果你知道你正在运行笛卡尔树的递归遍历，那么更容易看出你保证找到最大的矩形。此外，知道笛卡尔树的存在还可以为解决其他问题提供有用的工具。笛卡尔树出现在针对区间最小查询问题设计快速数据结构时，并用于将后缀数组转换为后缀树。
这是一些Java代码，它实现了这个思想，由@Azeem提供！
import java.util.Stack;
public class CartesianTreeMakerUtil {
private static class Node {
int val;
Node left;
Node right;
}
public static Node cartesianTreeFor(int[] nums) {
Node root = null;
Stack<Node> s = new Stack<>();
for(int curr : nums) {
Node lastJumpedOver = null;
while(!s.empty() && s.peek().val > curr) {
lastJumpedOver = s.pop();
}
Node currNode = this.new Node();
currNode.val = curr;
if(s.isEmpty()) {
root = currNode;
}
else {
s.peek().right = currNode;
}
currNode.left = lastJumpedOver;
s.push(currNode);
}
return root;
}
public static void printInOrder(Node root) {
if(root == null) return;
if(root.left != null ) {
printInOrder(root.left);
}
System.out.println(root.val);
if(root.right != null) {
printInOrder(root.right);
}
}
public static void main(String[] args) {
int[] nums = new int[args.length];
for (int i = 0; i < args.length; i++) {
nums[i] = Integer.parseInt(args[i]);
}
Node root = cartesianTreeFor(nums);
tester.printInOrder(root);
}
}
O(N) 中最简单的解决方案
long long getMaxArea(long long hist[], long long n)
{
stack<long long> s;
long long max_area = 0;
long long tp;
long long area_with_top;
long long i = 0;
while (i < n)
{
if (s.empty() || hist[s.top()] <= hist[i])
s.push(i++);
else
{
tp = s.top(); // store the top index
s.pop(); // pop the top
area_with_top = hist[tp] * (s.empty() ? i : i - s.top() - 1);
if (max_area < area_with_top)
{
max_area = area_with_top;
}
}
}
while (!s.empty())
{
tp = s.top();
s.pop();
area_with_top = hist[tp] * (s.empty() ? i : i - s.top() - 1);
if (max_area < area_with_top)
max_area = area_with_top;
}
return max_area;
}
min，那么每个值的左右极限是什么？min的最左边的值，以及同样小于当前min的第一个最右边的值。stack结构。还有一种使用分治算法的解决方案。其算法如下：
1）以最小高度为断点将数组分成两部分
2）最大面积是以下三者中的最大值： a）最小高度 * 数组大小 b）左半数组中的最大矩形 c）右半数组中的最大矩形
时间复杂度为O（nlogn）
我不理解其他条目，但我认为我知道如何以O(n)的方式执行以下操作。
A）对于每个索引，在该索引处结束的直方图内找到与索引列接触矩形顶部的最大矩形，并记住矩形开始位置。可以使用基于堆栈的算法在O(n)中完成此操作。
B）同样，对于每个索引，在该索引处开始的直方图内找到与索引列接触矩形顶部的最大矩形，并记住矩形结束位置。也可以使用与（A）相同的方法，在直方图向后扫描时以O(n)的速度完成。
C）对于每个索引，结合（A）和（B）的结果，确定该索引处的列接触矩形顶部的最大矩形。像（A）一样的O(n)。
D）由于最大矩形必须被直方图的某些列所接触，因此最大矩形是在步骤（C）中找到的最大矩形。
难点在于实现（A）和（B），我认为这就是JF Sebastian可能已经解决而不是所述一般问题。
我编写了这个代码，感觉稍微好一些：
import java.util.Stack;
class StackItem{
public int sup;
public int height;
public int sub;
public StackItem(int a, int b, int c){
sup = a;
height = b;
sub =c;
}
public int getArea(){
return (sup - sub)* height;
}
@Override
public String toString(){
return " from:"+sup+
" to:"+sub+
" height:"+height+
" Area ="+getArea();
}
}
public class MaxRectangleInHistogram {
Stack<StackItem> S;
StackItem curr;
StackItem maxRectangle;
public StackItem getMaxRectangleInHistogram(int A[], int n){
int i = 0;
S = new Stack();
S.push(new StackItem(0,0,-1));
maxRectangle = new StackItem(0,0,-1);
while(i<n){
curr = new StackItem(i,A[i],i);
if(curr.height > S.peek().height){
S.push(curr);
}else if(curr.height == S.peek().height){
S.peek().sup = i+1;
}else if(curr.height < S.peek().height){
while((S.size()>1) && (curr.height<=S.peek().height)){
curr.sub = S.peek().sub;
S.peek().sup = i;
decideMaxRectangle(S.peek());
S.pop();
}
S.push(curr);
}
i++;
}
while(S.size()>1){
S.peek().sup = i;
decideMaxRectangle(S.peek());
S.pop();
}
return maxRectangle;
}
private void decideMaxRectangle(StackItem s){
if(s.getArea() > maxRectangle.getArea() )
maxRectangle = s;
}
}
请注意：
Time Complexity: T(n) < O(2n) ~ O(n)
Space Complexity S(n) < O(n)
class Solution {
private class Node {
int val;
Node left;
Node right;
int index;
}
public Node getCartesianTreeFromArray(int [] nums) {
Node root = null;
Stack<Node> s = new Stack<>();
for(int i = 0; i < nums.length; i++) {
int curr = nums[i];
Node lastJumpedOver = null;
while(!s.empty() && s.peek().val >= curr) {
lastJumpedOver = s.pop();
}
Node currNode = this.new Node();
currNode.val = curr;
currNode.index = i;
if(s.isEmpty()) {
root = currNode;
}
else {
s.peek().right = currNode;
}
currNode.left = lastJumpedOver;
s.push(currNode);
}
return root;
}
public int largestRectangleUnder(int low, int high, Node root, int [] nums) {
/* Base case: If the range is empty, the biggest rectangle we
* can fit is the empty rectangle.
*/
if(root == null) return 0;
if (low == high) {
if(0 <= low && low <= nums.length - 1) {
return nums[low];
}
return 0;
}
/* Assume the Cartesian tree nodes are annotated with their
* positions in the original array.
*/
int leftArea = -1 , rightArea= -1;
if(root.left != null) {
leftArea = largestRectangleUnder(low, root.index - 1 , root.left, nums);
}
if(root.right != null) {
rightArea = largestRectangleUnder(root.index + 1, high,root.right, nums);
}
return Math.max((high - low + 1) * root.val,
Math.max(leftArea, rightArea));
}
public int largestRectangleArea(int[] heights) {
if(heights == null || heights.length == 0 ) {
return 0;
}
if(heights.length == 1) {
return heights[0];
}
Node root = getCartesianTreeFromArray(heights);
return largestRectangleUnder(0, heights.length - 1, root, heights);
}
}