理解主定理

Question

理解主定理

algorithmmaster-theorem

8

通用形式: T(n) = aT(n/b) + f(n)

因此，我必须比较 n^logb(a) 和 f(n)

如果 n^logba > f(n)，则为情况1，且T(n)=Θ(n^logb(a))

如果 n^logba < f(n)，则为情况2，且T(n)=Θ((n^logb(a))(logb(a)))

这样正确吗？还是我误解了什么？

那么第三种情况呢？它何时适用？

- a1204773

为什么投票关闭并对该主题进行了负评？这个主题不是离题的...更好地阅读FAQ...我的问题涵盖了软件算法类别... - a1204773

2个回答

5

我认为你误解了这个问题。如果n^logba > f(n)是情况1，且T(n)=Θ(n^logb(a))。在这里，你不需要担心f(n)的结果，你得到的是T(n)=Θ(n^logb(a))。 f(n)是T(n)的一部分，如果你得到了T(n)的结果，那么该值将包含f(n)。所以，没有必要考虑那部分。如果你还不清楚，请告诉我。

- AKS

网页内容由stack overflow 提供, 点击上面的

可以查看英文原文，
原文链接

- dharam · Accepted Answer

求解递归关系的主定理

递归关系在解决复杂问题的分治策略中经常出现。

它可以解决什么问题？

它可以解决形如 T(n) = aT(n/b) + f(n) 的递归关系。
a 应大于或等于1。这意味着问题至少被减小到一个更小的子问题。至少需要一次递归。
b 应大于1。这意味着每次递归时，问题的规模都会缩小。如果 b 不大于1，则说明我们的子问题不是更小的问题。
f(n) 对于相对较大的 n 值必须为正数。

请考虑下面的图片：

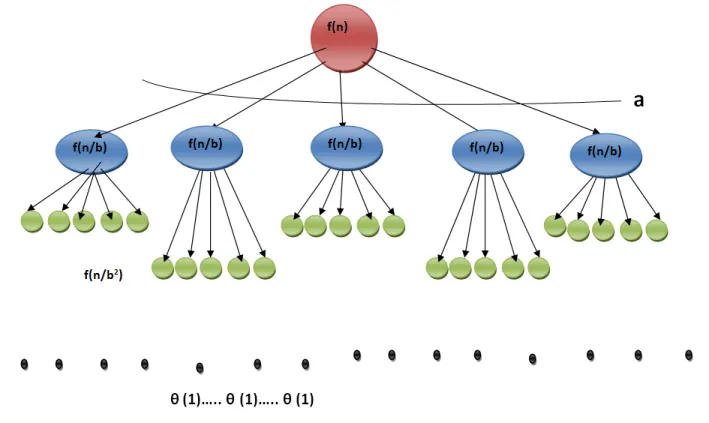
enter image description here

假设我们有一个大小为n的问题需要解决。每一步，问题可以分成a个子问题，每个子问题的大小都较小，大小减小了b倍。

简单来说，上述陈述意味着一个大小为n的问题可以被分成相对较小的a个子问题，每个子问题的大小为n/b。

此外，上图显示，当我们多次分割问题时，每个子问题都会变得非常小，可以在恒定时间内解决。

对于以下推导，请将log视为以b为底数。

假设H是树的高度，则H = logn。叶子节点的数量= a^logn。

一级所完成的总工作量：f(n)
二级所完成的总工作量：a * f(n/b)
三级所完成的总工作量：a * a * f(n/b2)
最后一级所完成的总工作量：叶子节点数 * θ(1)。这等于n^loga

主定理的三种情况

情况1：

假设每个级别操作的成本呈显著增长，到达叶子级别时，f(n)的值变得多项式地小于n^loga的值。那么整体运行时间将受到最后一级成本的严重支配。因此，T(n) = θ(n^loga)。

情况2：

假设每个级别上的操作成本大致相等。在这种情况下，f(n)大致等于n^loga。因此，总运行时间将是f(n)乘以总级数。

T(n) = θ(n^loga * logn)，其中k可以>=0。当k >= 0时，logn将是树的高度。

注意：这里的logn以k+1为底。

情况3：

假设每个级别上的操作成本都按照显著因子递减，并且到达叶级别时，f(n)的值变得多项式比n^loga大。那么整个运行时间将严重受到第一级别成本的影响。因此，T(n) = θ(f(n))。

如果你想了解更详细的阅读和练习示例，请访问我的博客文章 Master Method to Solve Recurrences。