这个朴素的计算组合代码的大O复杂度是多少？

Question

下面这个递归算法是计算组合数n选k的一种方式（效率相对较低）：

 int combinationsOf(int n, int k) {
     if (k == 0) return 1;
     if (n == 0) return 0;
     return combinationsOf(n - 1, k) + combinationsOf(n - 1, k - 1);
}

基于以下递归思路：

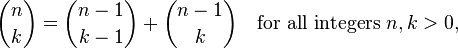
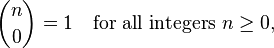
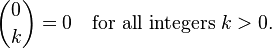
实际计算这个函数需要大量的函数调用。例如，使用这种方法计算2选2会进行以下调用：

 combinationsOf(2, 2)
   |  |
   |  +- combinationsOf(1, 2)
   |       |  |
   |       |  +- combinationsOf(0, 2)
   |       |
   |       +-- combinationsOf(1, 1)
   |             |  |
   |             |  +- combinationsOf(0, 1)
   |             |
   |             +- combinationsOf(1, 0)
   +- combinationsOf(2, 1)
        |  |
        |  +- combinationsOf(2, 0)
        |
        +- combinationsOf(1, 1)
             |  |
             |  +- combinationsOf(0, 1)
             |
             +- combinationsOf(1, 0)

有 许多 方法可以提高此函数的运行时间- 我们可以使用动态规划，使用闭式公式 nCk = n! / (k! (n - k)!）等。但是，我很好奇这个特定算法的效率有多低。

作为 n 和 k 的函数，此函数的大O时间复杂度是什么？

- templatetypedef

---

你应该返回 combinationsOf(n - 1, k - 1) + combinationsOf(n - 1, k)，不是吗？ - Blender

@Blender- 哦，糟糕！是的，已经修复了。 :-) - templatetypedef

Answer 1

让C(n,k)表示使用该方法计算binom(n,k)所需的成本，其中

C(0,_) = 1
C(_,0) = 1

作为基本情况。

循环显然是

C(n,k) = 1 + C(n-1,k-1) + C(n-1,k)

如果我们认为加法的成本为1。那么，我们可以轻松地检查出

             k
C(n,k) = 2 * ∑ binom(n,j) - 1
            j=0

通过归纳法，当 k >= n 时，代价为 2^(n+1) - 1，C(n,n-1) = 2^(n+1)- 3，C(n,1) = 2*n+1，C(n,2) = n*(n+1)+1。在此之后，我没有看到简洁的公式。

我们有一个明显的上界。

C(n,k) < 2^(n+1)

独立于k，对于k < n/2，我们可以粗略地估计。

C(n,k) <= 2*(k+1)*binom(n,k)

这个结果对于较小的k有更小的限制，因此总体而言

C(n,k) ∈ O(min{(k+1)*binom(n,min(k, n/2)), 2^n})

需要夹紧k的最小值，因为binom(n,k)在k > n/2时会减少到1。

- Daniel Fischer

---

也许我漏掉了什么，但如果k >= n，那么这个公式怎么简化为2^{n+1} - 1呢？如果k >= n，则二项式定理表明总和会减少到2^n，因此我们将得到1 + 2(2^n) = 1 + 2^{n+1}。符号如何翻转？ - templatetypedef

总和从“1”开始，而不是从“0”开始。我认为我应该更好地写成“2*∑ binom(n,j) - 1”，并让总和从0开始。 - Daniel Fischer

非常巧妙！一个问题 - 这到底是从哪里来的？我通过了归纳，但我不知道我怎么可能自己想出这个。 - templatetypedef

我刚刚制作了一个小表格（n，k <= 6），并查看了每行的差异。这样清晰明了地解决了问题。（我也查看了列之间的差异，但那些并没有那么有用。） - Daniel Fischer

Answer 2

O(2^n)

当n<k时，经过n个步骤后，通过命中n=0来停止递归。在每个递归层级中，您调用两个函数，因此这就是数字2的来源。如果n>k，则通过命中k=0来停止“右分支”中的递归，这比命中n=0少几步，但总体复杂度仍为2^n。

但真正的问题是递归本身 - 您很快就会达到堆栈限制。

- Strix

Answer 3

问题中显示的递归树与给定算法不符，它遵循 combinationsOf(n-1, k) + combinationsOf(n, k-1) 公式，而不是 combinationsOf(n-1, k) + combinationsOf(n-1, k-1)。这里显示的是正确的：

 combinationsOf(2, 2)
   |  |
   |  +- combinationsOf(1, 2)
   |      |  |
   |      |  +- combinationsOf(0, 2)
   |      |
   |      +-- combinationsOf(0, 1)
   |             
   +---- combinationsOf(1, 1)
          |  |
          |  +- combinationsOf(0, 1)
          |
          +- combinationsOf(0, 0)

给定这棵树，我们看到对于一个 (n, k) 的输入，递归树的节点数最多为 (n, n) 输入对应的递归树的节点数。
在最坏情况下分析，考虑 (n, n) 的输入。树的高度为 n，节点数为 2^n - 1。在给定的示例中，树的高度为 3，节点数为 7。
(n, n) 输入的递归调用次数为 2^n - 1，算法的最坏时间复杂度为 O(2^n)。
递归的指数复杂度使得算法不可行，即使在较小的 n, k 值下，时间成本也过高。

所有的输入都是正整数 (n, k)，并且 n, k 满足 n>=k。

- agimarco