首先,我想说的是,下面的解决方案是一种暴力方法,因此仅适用于规模较小的图形,即顶点或弧线不多的情况。
如果您有大型网络,则应参考一些更高级的算法,例如https://link.springer.com/article/10.1007/s40747-018-0079-7。
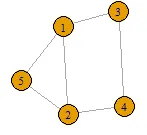
由于您有6个弧和5个顶点,因此您只需要从6个弧中删除2个弧即可找到生成树。这将产生
combn(6,2)个选项,您可以逐个删除这些边缘组合以检查是否仍然存在生成树。
Filter(
function(x) length(decompose(x)) == 1,
combn(
ecount(g),
ecount(g) - vcount(g) + 1,
FUN = function(x) delete.edges(g, E(g)[x]),
simplify = FALSE
)
)
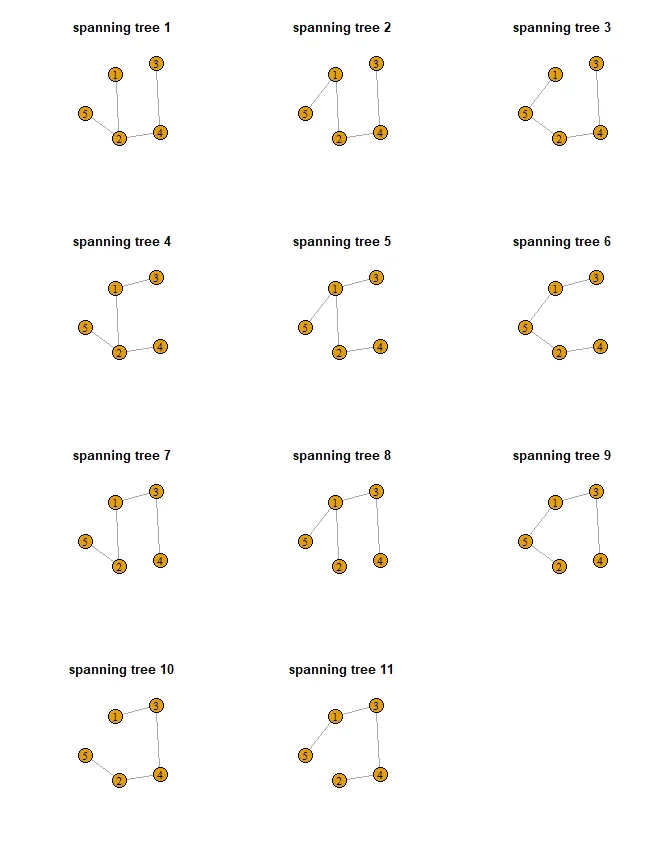
这将给出所有的11个生成树。
[[1]]
IGRAPH 9692f3d U--- 5 4 -- Erdos renyi (gnm) graph
+ attr: name (g/c), type (g/c), loops (g/l), m (g/n)
+ edges from 9692f3d:
[1] 2--4 3--4 1--5 2--5
[[2]]
IGRAPH 969368e U--- 5 4 -- Erdos renyi (gnm) graph
+ attr: name (g/c), type (g/c), loops (g/l), m (g/n)
+ edges from 969368e:
[1] 1--3 3--4 1--5 2--5
[[3]]
IGRAPH 969368e U--- 5 4 -- Erdos renyi (gnm) graph
+ attr: name (g/c), type (g/c), loops (g/l), m (g/n)
+ edges from 969368e:
[1] 1--3 2--4 1--5 2--5
[[4]]
IGRAPH 96938fa U--- 5 4 -- Erdos renyi (gnm) graph
+ attr: name (g/c), type (g/c), loops (g/l), m (g/n)
+ edges from 96938fa:
[1] 1--3 2--4 3--4 2--5
[[5]]
IGRAPH 96938fa U--- 5 4 -- Erdos renyi (gnm) graph
+ attr: name (g/c), type (g/c), loops (g/l), m (g/n)
+ edges from 96938fa:
[1] 1--3 2--4 3--4 1--5
[[6]]
IGRAPH 9693ded U--- 5 4 -- Erdos renyi (gnm) graph
+ attr: name (g/c), type (g/c), loops (g/l), m (g/n)
+ edges from 9693ded:
[1] 1--2 2--4 3--4 2--5
[[7]]
IGRAPH 969404b U--- 5 4 -- Erdos renyi (gnm) graph
+ attr: name (g/c), type (g/c), loops (g/l), m (g/n)
+ edges from 969404b:
[1] 1--2 2--4 3--4 1--5
[[8]]
IGRAPH 96942b7 U--- 5 4 -- Erdos renyi (gnm) graph
+ attr: name (g/c), type (g/c), loops (g/l), m (g/n)
+ edges from 96942b7:
[1] 1--2 1--3 3--4 2--5
[[9]]
IGRAPH 9694527 U--- 5 4 -- Erdos renyi (gnm) graph
+ attr: name (g/c), type (g/c), loops (g/l), m (g/n)
+ edges from 9694527:
[1] 1--2 1--3 3--4 1--5
[[10]]
IGRAPH 9694527 U--- 5 4 -- Erdos renyi (gnm) graph
+ attr: name (g/c), type (g/c), loops (g/l), m (g/n)
+ edges from 9694527:
[1] 1--2 1--3 2--4 2--5
[[11]]
IGRAPH 9694797 U--- 5 4 -- Erdos renyi (gnm) graph
+ attr: name (g/c), type (g/c), loops (g/l), m (g/n)
+ edges from 9694797:
[1] 1--2 1--3 2--4 1--5
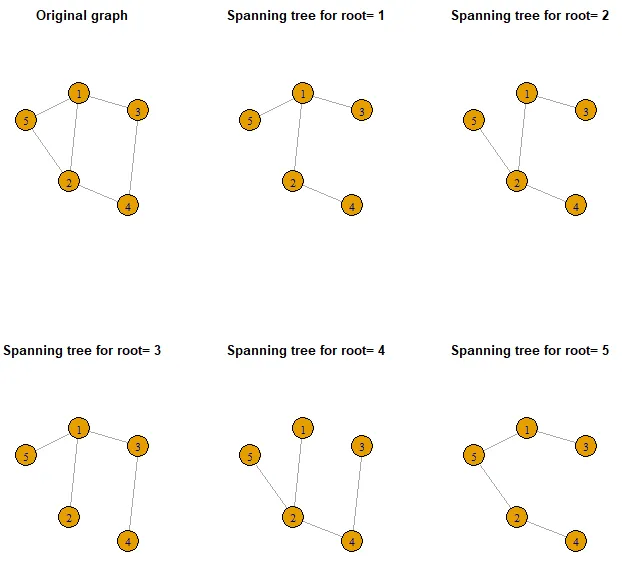
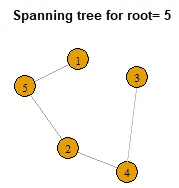
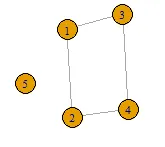
n = 5,所以最终得到5棵树。你有5个顶点,拉普拉斯矩阵的维度为5 x 5,并且有5个根节点用于广度优先搜索。 - Maurits Evers