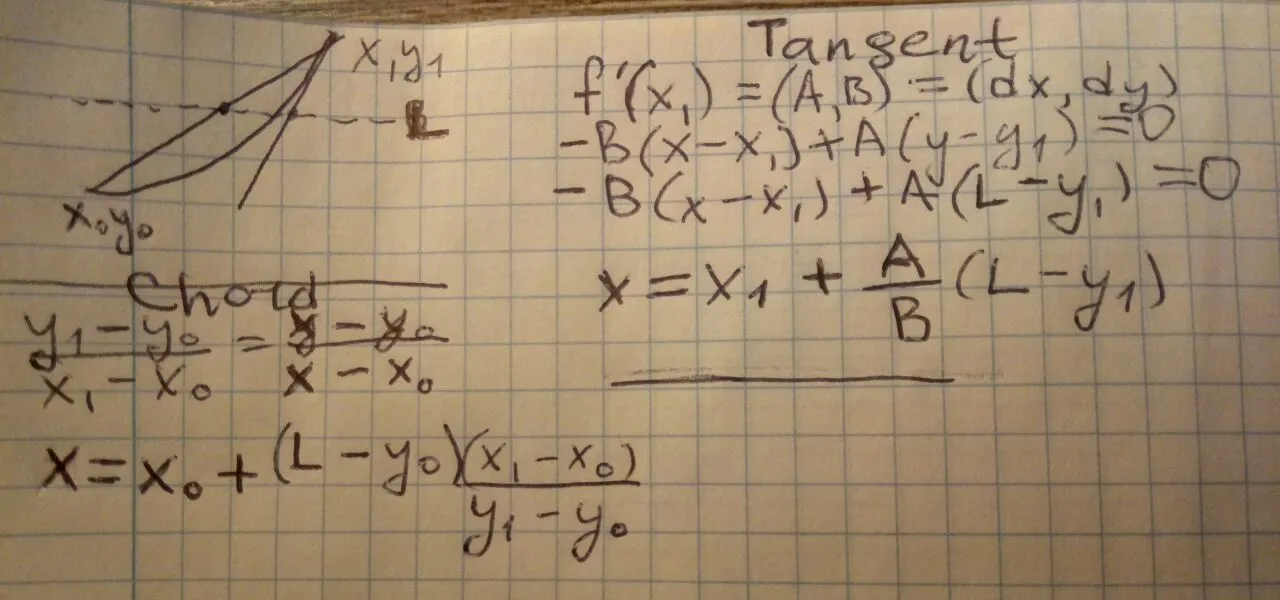我可以为解决您的任务提供四种方法。第一种基于
二分查找。第二种基于
牛顿迭代法。第三种基于
移位n次方根算法。第四种是我称之为弦切法,由我在
此处插入图片中描述。
许多答案中已经实现了二分查找。我在这里介绍自己对它及其实现的看法。
作为替代,我还实现了优化二分查找方法(标记为
Opt)。该方法从范围
[hi / 2, hi)开始,其中
hi等于
2^(num_bit_length / k),如果我们计算k次方根。
牛顿法是新方法,我看其他答案中没有实现。它通常被认为比二分查找更快,尽管我的代码计时结果并未显示加速。因此,这里提供这种方法只是作为参考/兴趣。
移位法比优化的二分查找方法快30-50%,如果在C ++中实现,应该会更快,因为C ++具有快速的64位算术,部分用于此方法。
弦切线法:
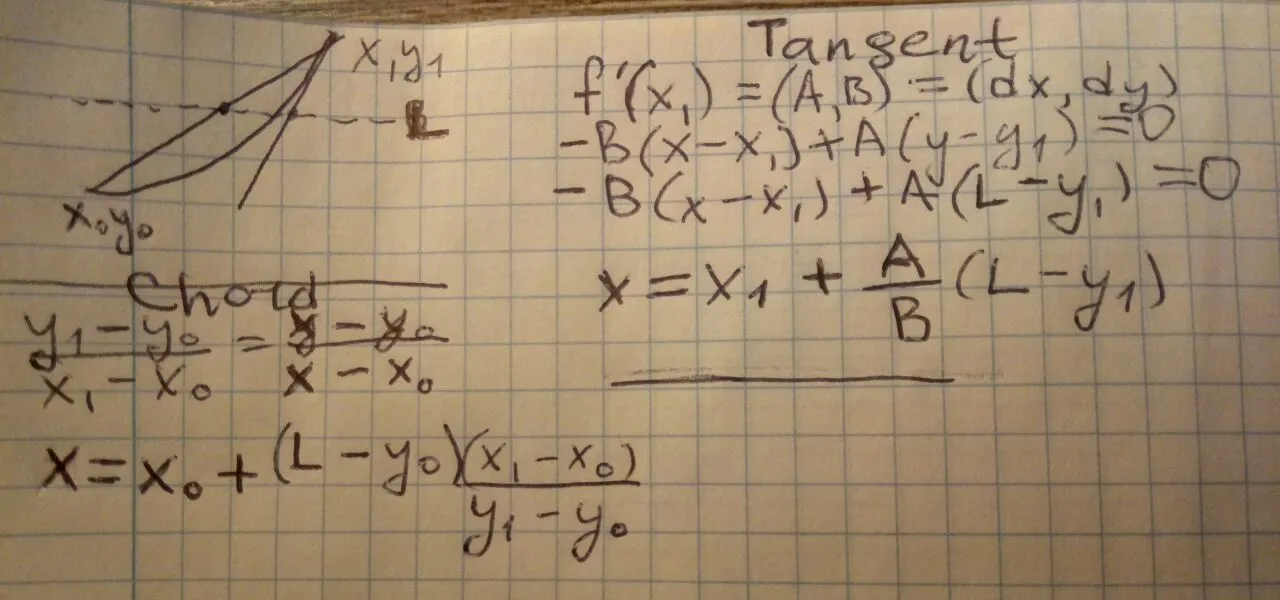
弦-切线法是由我发明的
(在纸上)(见上图),它受到牛顿法的启发并进行了改进。基本上,我画出一条
弦和一条
切线,并找到与水平线
y=n相交的点,这两个交点形成了根解
(x0,n)的下限和上限近似值,其中
n=x0 ^ k。这种方法被证明是最快的,而其他所有方法都需要超过2000次迭代,而这种方法只需要8次迭代,对于8192位数的情况。因此,这种方法比以前(按速度计算)的位移方法快
200-300倍。
例如,我生成了一个真正巨大的8192位随机整数。并测量使用这两种方法找到立方根的时间。
在
test() 函数中,您可以看到我将
k = 3 作为根的幂(立方根)传递,您可以传递任何幂而不是 3。
在线尝试!
def binary_search(begin, end, f, *, niter = [0]):
while begin < end:
niter[0] += 1
mid = (begin + end) >> 1
if f(mid):
begin = mid + 1
else:
end = mid
return begin
def binary_search_kth_root(n, k, *, verbose = False):
niter = [0]
res = binary_search(0, n + 1, lambda root: root ** k < n, niter = niter)
if verbose:
print('Binary Search iterations:', niter[0])
return res
def binary_search_opt_kth_root(n, k, *, verbose = False):
niter = [0]
hi = 1 << (n.bit_length() // k - 1)
while hi ** k <= n:
niter[0] += 1
hi <<= 1
res = binary_search(hi >> 1, hi, lambda root: root ** k < n, niter = niter)
if verbose:
print('Binary Search Opt iterations:', niter[0])
return res
def newton_kth_root(n, k, *, verbose = False):
f = lambda x: x ** k - n
df = lambda x: k * x ** (k - 1)
x, px, niter = n, 2 * n, [0]
while abs(px - x) > 1:
niter[0] += 1
px = x
x -= f(x) // df(x)
if verbose:
print('Newton Method iterations:', niter[0])
mini, minv = None, None
for i in range(-2, 3):
v = abs(f(x + i))
if minv is None or v < minv:
mini, minv = i, v
return x + mini
def shifting_kth_root(n, k, *, verbose = False):
B_bits = 64
r, y = 0, 0
B = 1 << B_bits
Bk_bits = B_bits * k
Bk_mask = (1 << Bk_bits) - 1
niter = [0]
for i in range((n.bit_length() + Bk_bits - 1) // Bk_bits - 1, -1, -1):
alpha = (n >> (i * Bk_bits)) & Bk_mask
B_y = y << B_bits
Bk_yk = (y ** k) << Bk_bits
Bk_r_alpha = (r << Bk_bits) + alpha
Bk_yk_Bk_r_alpha = Bk_yk + Bk_r_alpha
beta = binary_search(1, B, lambda beta: (B_y + beta) ** k <= Bk_yk_Bk_r_alpha, niter = niter) - 1
y, r = B_y + beta, Bk_r_alpha - ((B_y + beta) ** k - Bk_yk)
if verbose:
print('Shifting Method iterations:', niter[0])
return y
def chord_tangent_kth_root(n, k, *, verbose = False):
niter = [0]
hi = 1 << (n.bit_length() // k - 1)
while hi ** k <= n:
niter[0] += 1
hi <<= 1
f = lambda x: x ** k
df = lambda x: k * x ** (k - 1)
x_begin, x_end = hi >> 1, hi
y_begin, y_end = f(x_begin), f(x_end)
for icycle in range(1 << 30):
if x_end - x_begin <= 1:
break
niter[0] += 1
if 0:
x_mid = (x_begin + x_end) >> 1
y_mid = f(x_mid)
if y_mid > n:
x_end, y_end = x_mid, y_mid
else:
x_begin, y_begin = x_mid, y_mid
x_n = x_begin + (n - y_begin) * (x_end - x_begin) // (y_end - y_begin)
y_n = f(x_n)
tangent_x = x_n + (n - y_n) // df(x_n) + 1
chord_x = x_n + (n - y_n) * (x_end - x_n) // (y_end - y_n)
assert chord_x <= tangent_x, (chord_x, tangent_x)
x_begin, x_end = chord_x, tangent_x
y_begin, y_end = f(x_begin), f(x_end)
assert y_begin <= n, (chord_x, y_begin, n, n - y_begin)
assert y_end > n, (icycle, tangent_x - binary_search_kth_root(n, k), y_end, n, y_end - n)
if verbose:
print('Chord Tangent Method iterations:', niter[0])
return x_begin
def test():
import random, timeit
nruns = 3
bits = 8192
n = random.randrange(1 << (bits - 1), 1 << bits)
a = binary_search_kth_root(n, 3, verbose = True)
b = binary_search_opt_kth_root(n, 3, verbose = True)
c = newton_kth_root(n, 3, verbose = True)
d = shifting_kth_root(n, 3, verbose = True)
e = chord_tangent_kth_root(n, 3, verbose = True)
assert abs(a - b) <= 0 and abs(a - c) <= 1 and abs(a - d) <= 1 and abs(a - e) <= 1, (a - b, a - c, a - d, a - e)
print()
print('Binary Search timing:', round(timeit.timeit(lambda: binary_search_kth_root(n, 3), number = nruns) / nruns, 3), 'sec')
print('Binary Search Opt timing:', round(timeit.timeit(lambda: binary_search_opt_kth_root(n, 3), number = nruns) / nruns, 3), 'sec')
print('Newton Method timing:', round(timeit.timeit(lambda: newton_kth_root(n, 3), number = nruns) / nruns, 3), 'sec')
print('Shifting Method timing:', round(timeit.timeit(lambda: shifting_kth_root(n, 3), number = nruns) / nruns, 3), 'sec')
print('Chord Tangent Method timing:', round(timeit.timeit(lambda: chord_tangent_kth_root(n, 3), number = nruns) / nruns, 3), 'sec')
if __name__ == '__main__':
test()
输出:
Binary Search iterations: 8192
Binary Search Opt iterations: 2732
Newton Method iterations: 9348
Shifting Method iterations: 2752
Chord Tangent Method iterations: 8
Binary Search timing: 0.506 sec
Binary Search Opt timing: 0.05 sec
Newton Method timing: 2.09 sec
Shifting Method timing: 0.03 sec
Chord Tangent Method timing: 0.001 sec