嘈杂正弦时间序列中的实时峰值检测

Question

我一直在尝试实时检测正弦时间序列数据中的峰值，但到目前为止没有成功。我似乎找不到一个实时算法，可以以合理的准确度检测正弦信号中的峰值。要么无法检测到峰值，要么会检测到沿着正弦波的无数个点作为峰值。

对于类似正弦波的输入信号，并且可能包含一些随机噪声，有什么好的实时算法呢？

---

作为一个简单的测试案例，考虑一个静止的正弦波，它始终具有相同的频率和振幅。（确切的频率和振幅并不重要；我任意选择了60 Hz的频率，+/-1单位的振幅，以8 KS/s的采样率。）以下MATLAB代码将生成这样一个正弦信号：

dt = 1/8000;
t  = (0:dt:(1-dt)/4)';
x  = sin(2*pi*60*t);

使用Jean-Paul开发和发布的算法, 我要么检测不到峰值(左图), 要么检测到无数个"峰"(右图):

我已经尝试了各种可能的三个参数组合，按照Jean-Paul给出的"经验法则"进行尝试，但是到目前为止，我还没有得到我期望的结果。

---

我找到了一种替代算法，由Eli Billauer开发和发布，该算法能够给我想要的结果，例如：

{{尽管}}Eli Billauer的算法要简单得多，并且确实能够可靠地产生我想要的结果，但它不适用于实时应用。

---

作为我想应用这种算法的另一个信号的例子，考虑Eli Billauer为他自己的算法提供的测试案例：

t = 0:0.001:10;
x = 0.3*sin(t) + sin(1.3*t) + 0.9*sin(4.2*t) + 0.02*randn(1, 10001);

这是一种不太常见（不太均匀/规则）的信号，具有变化的频率和振幅，但仍然通常呈正弦波形。当绘制时，峰值很明显，但很难用算法识别。

---

什么是一个好的实时算法，可以正确地识别正弦输入信号中的峰值？当涉及到信号处理时，我并不是一个专家，因此获取一些考虑正弦输入的经验法则将会很有帮助。或者，也许我需要修改Jean-Paul算法本身，以便在正弦信号上正常工作。如果是这种情况，需要进行哪些修改，如何进行这些修改呢？

- Cody Gray

---

你的信号是纯正弦波还是包含其他噪声（例如Eli Billauer的情况）？ - Jean-Paul

@Jean-Paul 我对两种情况都很感兴趣... 实际上，我想在几个不同的应用程序中使用它。 - Cody Gray

问题不够清晰。它缺乏研究，而且是在寻求算法，而不是具体的问题。 - JoeCool-Avismón

Answer 1

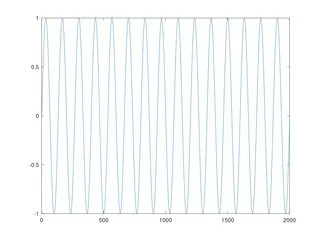
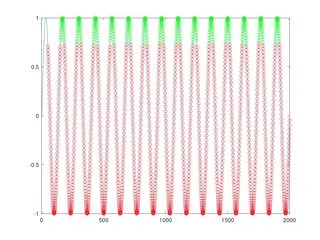
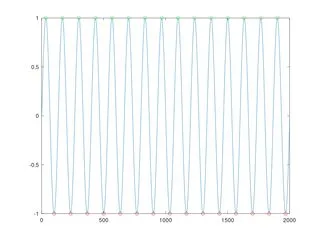
案例1：无噪声的正弦波

如果你的正弦波没有任何噪声，你可以使用非常经典的信号处理技术：取第一阶导数并检测其是否等于零。

例如：

function signal = derivesignal( d )

% Identify signal
signal = zeros(size(d));
for i=2:length(d)
    if d(i-1) > 0 && d(i) <= 0
        signal(i) = +1;     % peak detected
    elseif d(i-1) < 0 && d(i) >= 0
        signal(i) = -1;     % trough detected
    end
end

end

使用您提供的示例数据:

% Generate data
dt = 1/8000;
t  = (0:dt:(1-dt)/4)';
y  = sin(2*pi*60*t);

% Add some trends
y(1:1000) = y(1:1000) + 0.001*(1:1000)';
y(1001:2000) = y(1001:2000) - 0.002*(1:1000)';

% Approximate first derivative (delta y / delta x)
d = [0; diff(y)];

% Identify signal
signal = derivesignal(d);

% Plot result
figure(1); clf; set(gcf,'Position',[0 0 677 600])
subplot(4,1,1); hold on;
title('Data');
plot(t,y);
subplot(4,1,2); hold on;
title('First derivative');
area(d);
ylim([-0.05, 0.05]);
subplot(4,1,3); hold on;
title('Signal (-1 for trough, +1 for peak)');
plot(t,signal); ylim([-1.5 1.5]);
subplot(4,1,4); hold on;
title('Signals marked on data');
markers = abs(signal) > 0;
plot(t,y); scatter(t(markers),y(markers),30,'or','MarkerFaceColor','red');

这将产生以下结果：

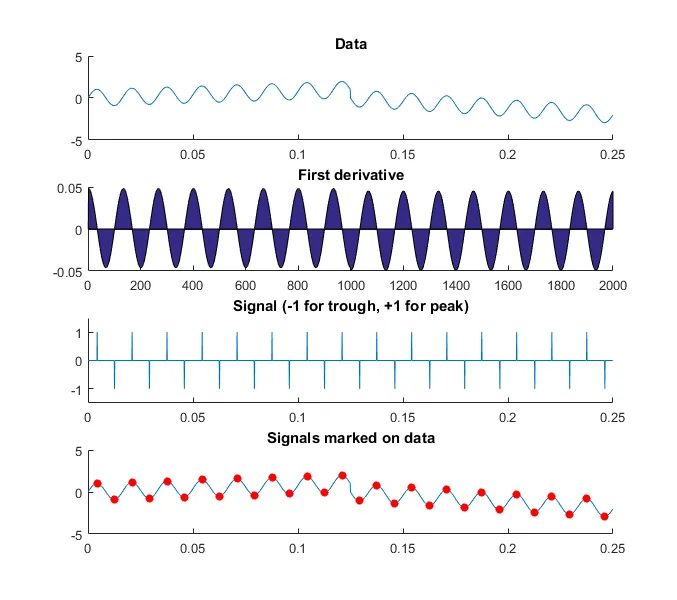
对于任何类型的正弦波，这种方法都非常有效，唯一的要求是输入信号不包含噪声。

---

情况2：带噪声的正弦波

一旦输入信号包含噪声，导数法就会失效。例如：

% Generate data
dt = 1/8000;
t  = (0:dt:(1-dt)/4)';
y  = sin(2*pi*60*t);

% Add some trends
y(1:1000) = y(1:1000) + 0.001*(1:1000)';
y(1001:2000) = y(1001:2000) - 0.002*(1:1000)';

% Add some noise
y = y + 0.2.*randn(2000,1);

下面的结果是由于“一阶差分放大了噪音”：

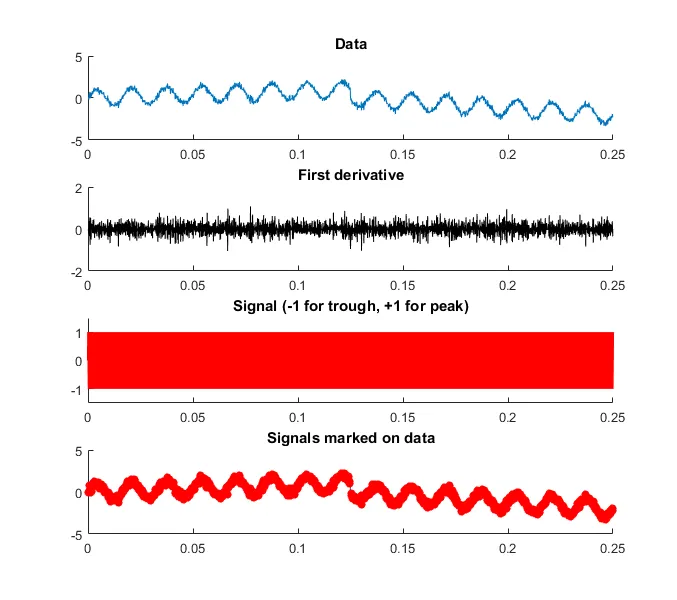
处理噪声的方法有很多种，最常用的方法是应用移动平均滤波器。移动平均滤波器的一个缺点是它们适应新信息的速度较慢，以至于信号可能会在出现后才被识别（移动平均滤波器具有滞后性）。

另一个非常典型的方法是使用Fourier分析来识别输入数据中的所有频率，忽略所有低振幅和高频率正弦波，并使用剩余的正弦波作为滤波器。剩余的正弦波将被（大部分）从噪声中清除，然后可以再次使用一阶差分来确定峰值和谷值（或对于单个正弦波，您知道峰值和谷值发生在相位的1/4和3/4π）。我建议您阅读任何一个信号处理理论书籍，以了解更多关于这种技术的信息。Matlab还有一些教育资料。

如果您想在硬件中使用此算法，我建议您也看看WFLC（加权傅里叶线性组合器）或使用例如1个振荡器或PLL（锁相环）来估计噪声波的相位，而不必进行完整的快速傅里叶变换。您可以在维基百科上找到数字锁相环的Matlab算法。

我会在这里建议稍微复杂一些的方法，以实时识别峰值和谷值：使用移动的最小二乘拟合将正弦波函数拟合到您的数据中，并使用Fourier分析的初始估计。

下面是我的函数：

function [result, peaks, troughs] = fitsine(y, t, eps)

% Fast fourier-transform
f = fft(y);
l = length(y);
p2 = abs(f/l);
p1 = p2(1:ceil(l/2+1));
p1(2:end-1) = 2*p1(2:end-1);
freq = (1/mean(diff(t)))*(0:ceil(l/2))/l;

% Find maximum amplitude and frequency
maxPeak = p1 == max(p1(2:end)); % disregard 0 frequency!
maxAmplitude = p1(maxPeak);     % find maximum amplitude
maxFrequency = freq(maxPeak);   % find maximum frequency

% Initialize guesses
p = [];
p(1) = mean(y);         % vertical shift
p(2) = maxAmplitude;    % amplitude estimate
p(3) = maxFrequency;    % phase estimate
p(4) = 0;               % phase shift (no guess)
p(5) = 0;               % trend (no guess)

% Create model
f = @(p) p(1) + p(2)*sin( p(3)*2*pi*t+p(4) ) + p(5)*t;
ferror = @(p) sum((f(p) - y).^2);
% Nonlinear least squares
% If you have the Optimization toolbox, use [lsqcurvefit] instead!
options = optimset('MaxFunEvals',50000,'MaxIter',50000,'TolFun',1e-25);
[param,fval,exitflag,output] = fminsearch(ferror,p,options);

% Calculate result
result = f(param);

% Find peaks
peaks = abs(sin(param(3)*2*pi*t+param(4)) - 1) < eps;

% Find troughs
troughs = abs(sin(param(3)*2*pi*t+param(4)) + 1) < eps;

end

如您所见，我首先对数据执行傅里叶变换，以找到振幅和频率的初始估计值。然后使用模型a + b sin(ct + d) + et将正弦波拟合到数据上。 拟合值代表一个正弦波，我知道+1和-1分别是峰值和谷值。 因此，我可以将这些值识别为信号。

对于具有（缓慢变化）趋势和一般（白色）噪声的正弦波，这种方法非常有效：

% Generate data
dt = 1/8000;
t  = (0:dt:(1-dt)/4)';
y  = sin(2*pi*60*t);

% Add some trends
y(1:1000) = y(1:1000) + 0.001*(1:1000)';
y(1001:2000) = y(1001:2000) - 0.002*(1:1000)';

% Add some noise
y = y + 0.2.*randn(2000,1);

% Loop through data (moving window) and fit sine wave
window = 250;   % How many data points to consider
interval = 10;  % How often to estimate
result = nan(size(y));
signal = zeros(size(y));
for i = window+1:interval:length(y)
    data = y(i-window:i);   % Get data window
    period = t(i-window:i); % Get time window
    [output, peaks, troughs] = fitsine(data,period,0.01);
    
    result(i-interval:i) = output(end-interval:end);
    signal(i-interval:i) = peaks(end-interval:end) - troughs(end-interval:end);
end

% Plot result
figure(1); clf; set(gcf,'Position',[0 0 677 600])
subplot(4,1,1); hold on;
title('Data');
plot(t,y); xlim([0 max(t)]); ylim([-4 4]);
subplot(4,1,2); hold on;
title('Model fit');
plot(t,result,'-k'); xlim([0 max(t)]); ylim([-4 4]);
subplot(4,1,3); hold on;
title('Signal (-1 for trough, +1 for peak)');
plot(t,signal,'r','LineWidth',2); ylim([-1.5 1.5]);
subplot(4,1,4); hold on;
title('Signals marked on data');
markers = abs(signal) > 0;
plot(t,y,'-','Color',[0.1 0.1 0.1]);
scatter(t(markers),result(markers),30,'or','MarkerFaceColor','red');
xlim([0 max(t)]); ylim([-4 4]);

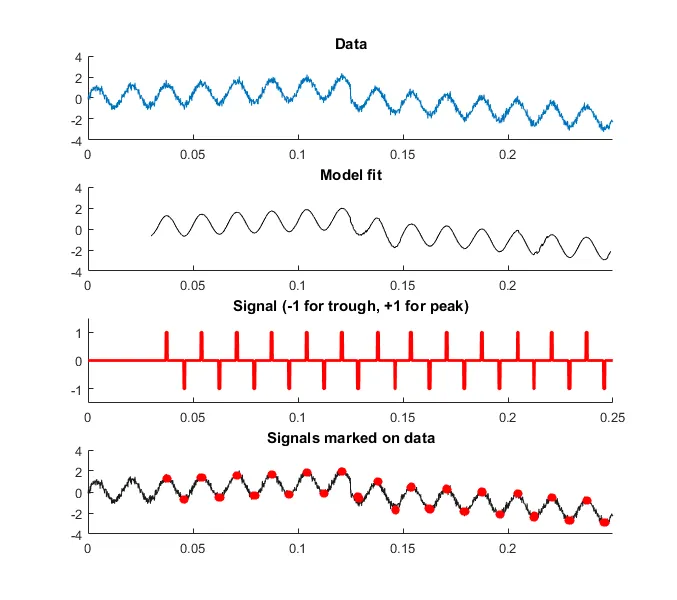
这种方法的主要优点是：

• 您可以获得实际数据模型，因此您可以在未来发生信号之前预测信号！（例如，固定模型并通过输入未来时间段来计算结果）
• 您不需要每个时间段都估计模型（请参见代码中的参数interval）

缺点是您需要选择一个回溯window，但您将使用任何用于实时检测的方法都会遇到此问题。

视频演示

Data是输入数据，Model fit是拟合到数据的正弦波（请参见代码），Signal表示峰值和谷值，Signals marked on data给出了算法的准确性印象。 注意：观察模型适应图中趋势的方式！

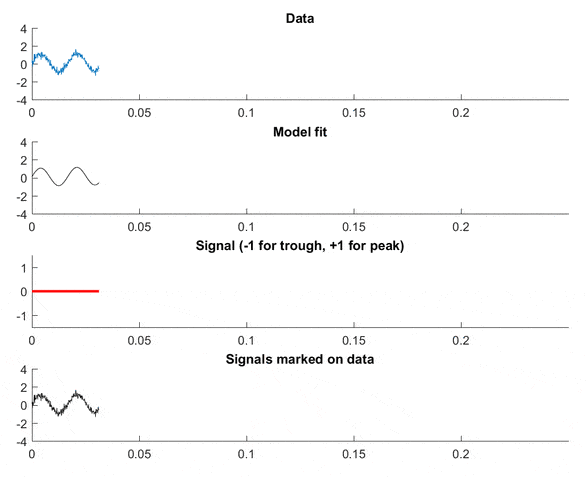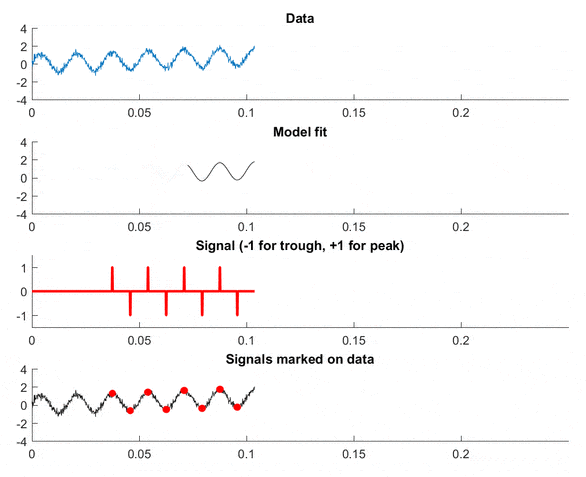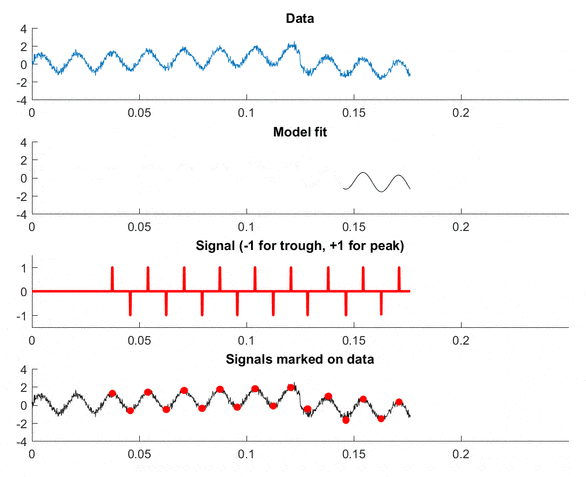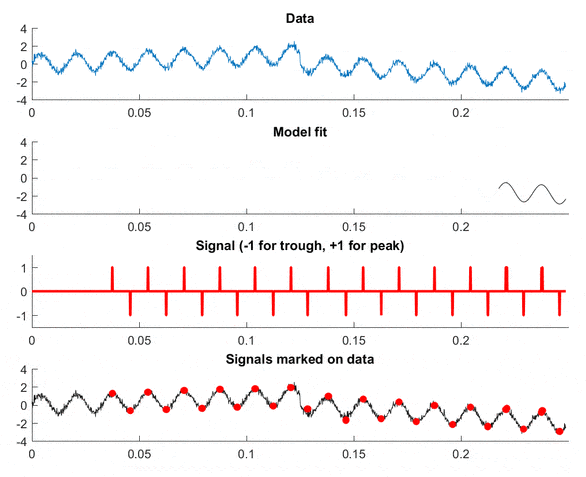
这应该能帮助您入门。还有很多关于信号检测理论的优秀书籍（只需谷歌这个词），它们将深入探讨这些类型的技术。祝好运！

- Jean-Paul

Answer 2

考虑使用findpeaks，它速度快，这对于实时性可能很重要。您应该过滤高频噪声以提高准确性。在这里，我使用移动窗口平滑数据。

t = 0:0.001:10;
x = 0.3*sin(t) + sin(1.3*t) + 0.9*sin(4.2*t) + 0.02*randn(1, 10001);
[~,iPeak0] = findpeaks(movmean(x,100),'MinPeakProminence',0.5);

你可以计时这个进程（0.0015秒）。

f0 = @() findpeaks(movmean(x,100),'MinPeakProminence',0.5)
disp(timeit(f0,2))

相比之下，处理斜率只快了一点点（0.00013秒），但findpeaks有许多有用的选项，例如峰值之间的最小间隔等。

iPeaks1 = derivePeaks(x);
f1 = @() derivePeaks(x)
disp(timeit(f1,1))

derivePeaks 是什么：

function iPeak1 = derivePeaks(x)
xSmooth = movmean(x,100);
goingUp = find(diff(movmean(xSmooth,100)) > 0);
iPeak1 = unique(goingUp([1,find(diff(goingUp) > 100),end]));
iPeak1(iPeak1 == 1 | iPeak1 == length(iPeak1)) = [];
end

- Yuval Harpaz