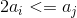贪心算法的正确性

Question

在非递减（正）整数序列中，当时，可以从该序列中删除两个元素。最多可以从此序列中删除多少对元素？

因此，我想到了以下解决方案：

• 将给定序列分为两部分（第一部分和第二部分）。
• 为它们中的每一个分配迭代器 - 分别为it_first := 0和it_second := 0，count := 0
• 当it_second != second.length时
  • 如果2 * first[it_first] <= second[it_second]
    • count++，it_first++，it_second++
  • 否则
    • it_second++
• count就是答案

例子:

count := 0

[1,5,8,10,12,13,15,24] --> first := [1,5,8,10], second := [12,13,15,24]

1. 2 * 1 ?< 12 --> true, count++, it_first++ and it_second++

2. 2 * 5 ?< 13 --> true, count++, it_first++ and it_second++

3. 2 * 8 ?< 15 --> false, it_second++

4. 8 ?<24 --> true, count ++it_second reach the last element - END.

5. count == 3

线性复杂度（最坏情况下没有要删除的元素。n/2个元素与n/2个元素进行比较）。 所以我的缺失部分是算法的“正确性”-我已经读了关于贪心算法证明的文章-但大多数都是树，我找不到类比。任何帮助将不胜感激。谢谢！

编辑：

通过正确性，我指的是： *它可以正常工作 *它无法更快地完成（在logn或常数中） 我想放置一些图形，但由于声望点数＜10-我不能。 （我指的是一开始的一个latex）

- lemoid

---

你的方法并不能覆盖所有情况。比如 [1, 2, 4, 9]，[4, 9] 也可以是这样的一对。或者像你的例子中，[12, 24] 也可以是这样的一对。 - Harsh Gupta

不要紧。我们询问最多可以移除多少对。 - lemoid

我在询问如何证明算法的正确性。我的意思是：它不能更好地完成（在常数时间或logn中），并且总是找到正确的解决方案。如果我没有表达清楚，那么请见谅。 - lemoid

@DragosRizescu - 我指的是我的贪心算法给出的解决方案。 - lemoid

我的第一次尝试将会是反证法。 - greybeard

Answer 1

1. 正确性：

   • 假设最多可以删除的数对数量为k。声明：存在一个最佳解，其中所有数对的第一个元素是数组中k个最小元素。 证明：我将展示如何将任何解转换为包含前k个元素作为所有数对的第一元素的解。

     1. 假设我们有两个数对(a, b)，(c, d)，使得a <= b <= c <= d，2 * a <= b和2 * c <= d。在这种情况下，数对(a, c)和(b, d)也是有效的。现在我们有a <= c <= b <= d。因此，我们总是可以以这样的方式转换出数对，即任何数对的第一个元素都不大于任何数对的第二个元素。

     2. 当我们具备了这个特性后，我们可以简单地用数组中最小的第一个元素替换所有数对的第一个元素中最小的元素，用数组中第二小的第一个元素替换所有数对的第一个元素中第二小的元素，以此类推，而不会使任何数对无效。

   • 现在我们知道了存在一个包含k个最小元素的最佳解。显然，通过选取每个符合条件的最小未使用元素(使其变大只能减少下一个元素的答案)我们不能使答案更糟糕。因此，该解是正确的。

   • 关于数组长度为奇数的情况的说明：中间元素放在哪里都没有关系：放在第一半中是没用的(第二半中没有足够的元素)。如果我们将它放在第二半中，也是没用的(假设我们把它拿走了。这意味着第二半区间中有“空余”空间。因此，我们可以将某些元素向左移动一个位置，并摆脱它)。

2. 时间复杂度的最优性：这个算法的时间复杂度为O(n)。在最坏的情况下，我们无法在读取整个输入之前找到答案，并且读取已经需要O(n)时间。因此，这个算法是最优的。

- kraskevich

---

非常好。希望你喜欢那个。谢谢！ - lemoid

好的，我想我可以停止输入我的回复了 :) - Jeremy West

实际上，我们可以提出一个更强的断言：如果存在长度为k的有效答案，则取前k个值并将它们与最后k个值配对的答案也是有效的。然而，使用这个更强的断言似乎并不比运行所提出的算法更容易。 - Gassa

@Gassa 那正是我打算采用的方法。实际上，我认为这使证明更加清晰。但并不清楚它是否使算法更简单。 - Jeremy West

@JeremyWest 我也是 :) - Gassa

2. 的重要性在于产生正确结果的算法是 终止 的。 - greybeard

Answer 2

假设您的方法。索引从0开始。

通常表示：

• end_1 = floor(N/2) 第一部分的边界（包括在内）。

迭代时表示：

• i 是第一部分中的索引，j 是第二部分中的索引，
• 到目前为止的最优解 sol(i,j)（使用前面的算法），
• 剩余需要最优配对的对数，在点 (i,j) 后面，即从 (i+1,j+1) 开始的 rem(i,j)（可以使用后面的算法计算），
• 最终的最优解可以用任何一点的函数表示为 sol(i,j) + rem(i,j)。

Observation #1：当从前面开始进行算法时，使用范围为[0,i]的所有点，而[end_1+1,j]范围内的一些点未被使用（我们跳过了不够大的a(j)）。当从后面开始进行算法时，[i+1,end_1]中的一些点未被使用，并且使用了所有[j+1,N]点（我们跳过了不够小的a(i)）。

Observation #2：因为rem(i,j) = rem(i,j+1) + M，其中M可以是0或1，这取决于我们是否可以将a(j)与[i+1,end_1]范围内的某个未使用的元素配对。所以rem(i,j) >= rem(i,j+1)。 论证（反证法）：假设2*a(i) <= a(j)，并且不将a(i)和a(j)配对可以得到至少与配对后一样好的最终解。根据算法，我们接下来会尝试将a(i)和a(j+1)配对。由于：

• rem(i,j) >= rem(i,j+1)（见上文），
• sol(i,j+1) = sol(i,j)（因为我们没有将a(i)和a(j)配对），

我们得到sol(i,j) + rem(i,j) >= sol(i,j+1) + rem(i,j+1)，这与假设相矛盾。

- plesiv