以下是一个
O(n) 的解决方案,还可以为每个段指定可选的权重。
我们通过它与 X 轴的角度(a)和权重(w)来模拟每个段。此时,段的方向并不重要,任何值模 180° 都可以。思路是循环每个段,并跟踪到目前为止计算出的平均方向;并使用更接近平均自身的方向模 180 来调整此平均值。
伪代码(所有角度以度为单位):
aa = 0
ww = 0
for a, w in segments:
// Compute delta between angles in range [-180°..+180°[
da = a - aa
if da < -180:
da += 360
if da >= 180:
da -= 360
// Optional direction swap, delta in [-90°..+90°[
if da < -90:
da += 180
if da >= 90:
da -= 180
// The following formula also make sure aa = a mod 180
// when ww = 0 (first iteration).
aa += da * w / (w + ww)
ww += w
// Clamp result to [0°..+360°[
if aa >= 360:
aa -= 360
if aa < 0:
aa += 360
// Clamp final result aa to [0..+180°[ (optional step)
if aa > 180:
aa -= 180
我没有证明结果与迭代顺序无关,但是根据算法的第一眼印象,它应该是无关的。
关于算法与输入迭代顺序的依赖性
对于规范的输入数据,无论迭代顺序如何,该算法都非常稳定。
然而,一旦输入数据没有明确的主方向,该算法的结果将强烈依赖于迭代顺序,以难以预测的混沌模式出现。
数值模拟表明,对于标准差小于20°(中位数左右)的随机方向,该算法似乎总是稳定的。当标准差大于20°时,数值不稳定性开始出现,结果强烈依赖于迭代顺序(在20°到30°之间,差异可能足够小可以忽略,超过30°后差异变得很大)。
我没有精确计算混沌/稳定标准差截止值,因此将这个20°值作为初始猜测。一个精确的数学解决方案留给读者作为练习。
以下是数值模拟的结果(对于每个标准差从0到45°,在给定标准差的各种随机数据上运行1000次算法,并测量10次运行之间的平均差异)。
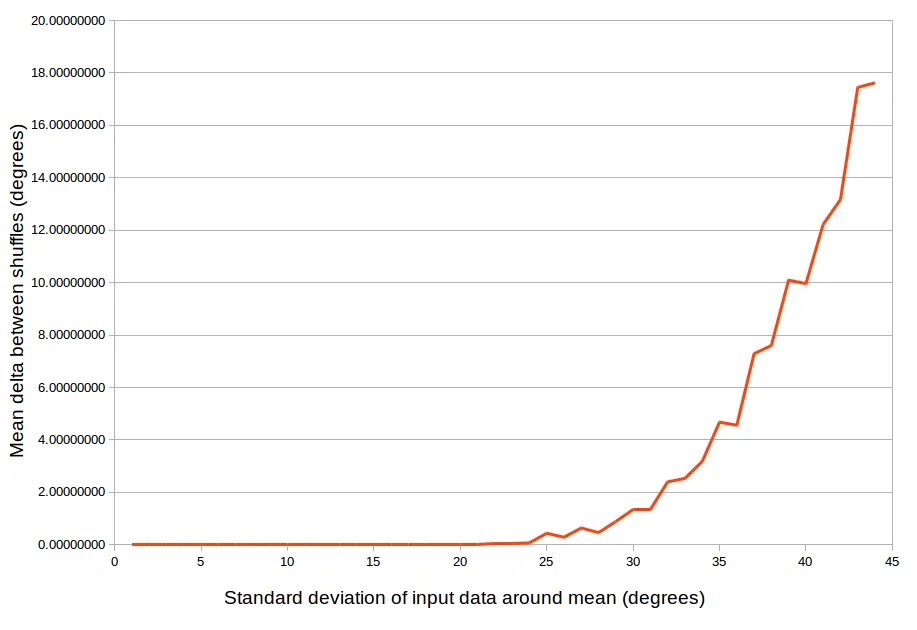
因此,为了获得最佳结果,如果您的输入数据不能保证具有小的标准偏差,则最好按稳定的关键字排序输入数据(首先是更大的权重,或者根据您的输入选择任何其他关键字)。
