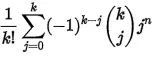将集合分区，使笛卡尔积满足约束条件

Question

我正在阅读这个问题，它描述了以下问题陈述：

给定两个整数：N和K。Lun狗对满足以下条件的字符串感兴趣：

- 字符串恰好有N个字符，每个字符都是'A'或'B'。 - 字符串s恰好有K个对(i,j) (0 <= i < j <= N-1)，使得s[i]='A'且s[j]='B'。

如果存在满足条件的字符串，则找到并返回任何一个这样的字符串。否则，返回一个空字符串

我想到这个问题等价于：

确定是否存在任何2分区0...N-1，其中笛卡尔积包含恰好K个元组(i,j)，其中i其中，元组元素表示将字符串索引分配给字符A和B。

---

这会产生非常朴素（但正确）的实现：

• 确定集合0...N-1的所有2部分划分
• 对于每个这样的划分，生成子集的笛卡尔积
• 对于每个笛卡尔积，计算元组(i, j)的数量，其中i < j
• 选择任何此计数为K的2部分划分

以下是JS的实现：

const test = ([l, r]) =>
  cart(l, r).reduce((p, [li, ri]) => p + (li < ri ? 1 : 0), 0) === k

const indices = _.range(0, n)
const results = partitions(indices).filter(test)

您可以在这里的原始问题上下文中测试结果。一些n = 13，k = 29的示例输出：

"aababbbbbbbbb", "babaaabbbbbbb", "baabababbbbbb", "abbaababbbbbb", ...

---

仅仅第一步的复杂度就是将集合划分的方法数：这是非常困难的第二类斯特林数 S(n, k)，其中k = 2：

例如，对于n=13，结果为4095，这并不理想。

显然，如果我们只需要一个满足要求的单个划分（这就是原问题所要求的），并且进行所有计算时都懒惰地进行，通常情况下我们不会进入最坏情况。但是总体而言，这种方法似乎仍然非常浪费，因为我们计算的大多数分区从未满足具有i＜j的笛卡尔积中的k元组的属性。

我的问题是是否有一些进一步的抽象或同构可以被识别出来以使其更加高效。例如，是否可能构造一个2-分区的子集，以便笛卡尔积上的条件在构造时得到满足？

- Asad Saeeduddin

---

只是一个非常一般的想法：在这些字符串上找到一些“算术中性”的操作。例如，对于您的13和29以及字符串1和4的示例：通过将第二个a更改为b，可以通过将位置5和7从b更改为a来进行补偿。如果您可以在所有等效字符串上找到（部分）顺序，并通过这些转换以系统化的方式遍历它，那么您只需要找到最小的字符串，然后从那里开始工作，而无需执行所有“浪费”的步骤。 - Peter Leupold

@PeterLeupold 这是一个非常好的想法。最初我希望能够发现所有可接受的字符串只是彼此旋转，但不幸的是关系更加复杂（如果确实存在）而且我无法识别任何东西。 - Asad Saeeduddin

我假设您可以通过将一些B向左移动并通过将其他B向右移动来补偿，只要它们不相互跳过，就可以将具有特定数量A和B的解转换为具有相同数量A和B的每个解。 - m69 ''snarky and unwelcoming''

@m69 这可能暗示了关于索引总和的某种不变量（也许是模求和？）。 - Asad Saeeduddin

移动哪些B向左或向右似乎并不重要？在任何情况下，将两个B相反方向移动1步会导致B“交叉”，结果字符串与之前的相同。 - Asad Saeeduddin

Answer 1

(这是一种通过算法构建所有解决方案的方法; 您可能正在寻找更数学化的方法。)

在此答案中，我提供了一种查找字典顺序最小解决方案的方法。这告诉您可以用多少个B构造一个解决方案。如果您将该方法倒过来，并从左侧添加A到一个由所有B组成的字符串中，则可以找到可以用多少个B构造解决方案的最大数量。

要在此范围内构造特定数量B的所有解决方案，可以再次使用递归方法，但是除了仅向末尾添加B并使用N-1递归一次之外，您还需要添加B，然后BA，然后BAA ... 并使用将产生有效解决方案的所有情况进行递归。再次考虑N = 13和K = 29的示例，其中B的最小数量为3，最大数量为10; 您可以像这样构造所有4个B的解决方案：

N=13 (number of digits)  
K=29 (number of pairs)  
B= 4 (number of B's)  

(13,29,4) =

(12,20,3) + "B"  
(11,21,3) + "BA"  
(10,22,3) + "BAA"  

此时，您已经知道您已经到达了不会产生解决方案的情况的末尾，因为(9/2)² < 23。所以在每个级别上，您都要使用以下递归：

N = N - length of added string  
K = K - number of A's still to be added  
B = B - 1  

当递归层数达到B为1或N-1时，您可以不进行进一步递归即可构建字符串。

实际上，您所做的是从最右边开始使用B，然后逐个将它们向左移动，同时通过将其他B向右移动来进行补偿，直到达到B尽可能靠左的位置。请参见此代码片段的输出：

function ABstring(N, K, B, str) {
    if ((N - B) * B < K) return;
    str = str || "";
    if (B <= 1 || B >= N - 1) {
        for (var i = N - 1; i >= 0; i--)
            str = (B == 1 && i == K || B == N - 1 && N - 1 - i != K || B == N ? "B" : "A") + str;
        document.write(str + "<br>");
    } else {
        var prefix = "B";
        --B;
        while (--N) {
            if (K - (N - B) >= 0 && B <= N)
                ABstring(N, K - (N - B), B, prefix + str);
            prefix += "A";
        }
    }
}
ABstring(13, 29, 4);

如果您对B的所有值从3到10运行此代码，则可以获得（N，K）=（13,29）的所有194个解决方案。而不是首先计算B的最小和最大数量，您可以将此算法应用于B从0到N的所有值（并在不再获得解决方案时停止）。

---

这是(N,K,B) = (16,24,4)的模式：

- m69 ''snarky and unwelcoming''

Answer 2

让P为一个函数，对于给定的AB字符串返回好的对数(i, j)，s[i] = 'A'，s[j] = 'B'。

首先考虑长度为N且B's数量固定的字符串，比如说b。包含(N-b)个A's的字符串。将这组字符串称为S_b。在S_b上最小的P值为0，所有的B's都在左边（将这个字符串称为O）。在S_b上最大的P值为b*(N-b)，所有的B's都在右边。这是一个简单的检查方法，用于确认在S_b中不存在具有所需属性的s。

考虑交换相邻的BA -> AB操作。该操作将P更改为+1。仅使用该操作，从字符串O开始，可以构造具有b个B's的每个字符串。这给我们带来了一个结论：如果b*(N-b) >= K，则在S_b中存在所需属性的s。 O中最右边的B可以移动到字符串的末尾，即N-b个位置。由于不可能交换两个B's，因此位于最右边的B左侧的B可以像最右边的B一样移动，...B's（m_i）可以进行的移动次数为0 <= m_1 <= m_2 <= ... <= m_b <= N-b。

因此，找到所有长度为N的AB字符串s，其中b个B's且P(s)=K等价于在最多b个部分中找到整数K的所有分区，其中每个部分都是<= N-b。要找到所有字符串，需要检查所有满足b*(N-b) >= K的b。

- Ante