logo标签列表

在N维空间中，计算距离3个点最近的等距点。

geometrycomputational-geometry
3
我正在尝试在任意维度中编写Ritter的包围球算法，但我卡在了创建一个球的部分，这个球的边缘上有3个给定点，或者换句话说，由N维空间中的3个点定义的球。

该球的中心将是从（定义）3个点到最小距离等距点。
我知道如何在2D中解决它（由3个点定义的三角形的外心），并且我已经看到了一些3D向量计算，但我不知道N-D的最佳方法是什么，甚至是否可能。
（如果我走错方向，我也会感激任何关于ND中最小包围球计算的建议。）
1
这似乎更像是一个数学问题，而不是一个编码/编程问题。这可能在Mathematica上更好。 - Matt
该链接并未提及由三个点确定的球体，而是包含一个球体和一个不在其内部的点的球体。新球体的中心位于从旧中心到外部点的直线上，即该点与球体上对极点的中点处。 - user1196549
问题的标题与内容不同。我认为你需要找到一个等距离点，同时最小化距离。请尝试编辑问题，更清楚地表达你真正想做什么。 - agentp
@george 你是对的。抱歉。 - ErroneousFatality
@YvesDaoust，请问您有证据证明这将是最小边界球中心吗？ - ErroneousFatality
显示剩余3条评论
2个回答
3
所以如果我理解正确：
所求点 p 是三个半径相同的超球体在你的点 p0，p1，p2 上的交点，半径 r 是所有可能解的最小值。在n维空间中，任意点被定义为（x1，x2，x3，...xn） 因此解决以下方程：
|p-p0|=r
|p-p1|=r
|p-p2|=r

其中p，r是未知量，p0，p1，p2是已知量。这导致了3*n个方程和n+1个未知量。因此，获取所有非零的r解并选择最小值。为了正确计算，请从每个球体中选择一些非平凡方程(0=r)来形成n+1个方程和n+1个未知量的系统，并解决它。

[注]

为了简化处理，您可以按照以下形式编写方程：

(p.xi-p0.xi)^2=r^2

在找到解（忽略负半径）之后，只使用 sqrt(r^2)。

还有一种更简单的方法：

您可以计算点 p0,p1,p2 所在平面，然后在该平面上查找这些点的 u,v 坐标。接着，在 (u,v) 坐标系中解决问题，最后将找到的解从 (u,v) 转换为 n-D 空间。

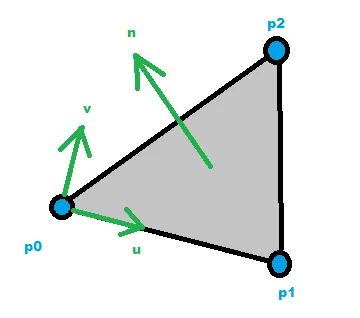
平面u，v坐标

n=(p1-p0)x(p2-p0); // x is cross product
u=(p1-p0); u/=|u|;
v=u x n; v/=|v|; // x is cross product

如果我的记忆没有出错，那么将 n-D -> u,v 进行转换的方法如下：

P0=(0,0);
P1=(|p1-p0|,0);
P2=(dot(p2-p0,u),dot(p2-p0,v));

其中P0,P1,P2 是平面上 p0,p1,p2 在 n-D 空间中对应的 2D 点在坐标系（u,v）中的投影。

反向转换如下所示:

p=(P.u*u)+(P.v*v);
哇，谢谢。这帮了我很多！我会尝试实现它！ - ErroneousFatality
1
网页内容由stack overflow 提供, 点击上面的
可以查看英文原文，
原文链接