我在阅读关于寻找最小生成树（对于加权图）和判断一个图是否存在哈密顿路径（依赖于哈密顿回路的存在）的算法时一脸懵逼。那么哈密顿路径和生成树之间有什么区别呢？它们都覆盖了图中所有的顶点。虽然我们可以使用高效的算法来寻找生成树（也许是最小生成树），但为什么我们不能寻找哈密顿回路的算法呢？我们可以不断地添加和删除边缘，直到形成一个环路，并且或许能够找到一个哈密顿回路吗？
5个回答
11
这两个问题有很大的不同。把最小生成树看作是连接地点的问题，您只需要支付一次建造道路的费用，但可以无限次使用它。通过 Kruskal 算法等方式，很容易得出允许您从任何地方到达任何其他地方的最便宜的道路配置。
另一方面，Hamiltonian Cycle 旨在最小化实际旅行距离，即每次移动都算入其中。（它还要求您不要重复访问某个地方，但这只是一个细节问题。）这个问题在本质上是非局部的，也就是说，您不能仅通过局部探索下一步的选项来确定您正在做正确的事情。相比之下，贪心的最小生成树算法保证在每一步选择要添加到树中的正确下一条边。
顺便说一句，“我们不能为 HP 找到有效的算法”是没有人说过的。可能只是我们还没有找到而已 :-)
- Kerrek SB
5
这并不是真的，因为有克里斯托菲德算法可以解决旅行商问题，并保证结果在最优解的3/2以内。哈密顿回路问题是旅行商问题的一种（廉价）近似方法。也许使用空间填充曲线会更容易些。 - Micromega
根据Wikipedia的说法，Christofides算法仅适用于欧几里得加权图。当然，有许多特殊情况下可以高效地完成TSP或HP。 - Kerrek SB
Kerrek：您是指它必须满足三角不等式吗？这里有一个链接http://www.scribd.com/doc/19417995/Euclidean-vs-nonEuclidean-Geometry。但我想不出一个真实世界的应用？您介意告诉我更多吗？您是否检查三角不等式？ - Micromega
是的，三角不等式意味着您的图形在欧几里得空间中等距存在。从中获得了一些局部信息，因为您知道A->B->C始终至少需要与A->C一样长的时间，在一般加权图中您并不知道这一点。例如，如果A->B和B->C的成本为1，但A->C的成本为10，则通过将AC替换为ABC来改进，但在欧几里得假设下，您永远不需要测试该做法。 - Kerrek SB
顺便说一下，这与微分几何意义上的“非欧几何”无关。后者意义上的几何学在本地总是满足三角不等式；只是不需要在本地是平坦的。 - Kerrek SB
6
这两个问题都需要连接所有的顶点。
对于最小生成树，你不关心将顶点 a 连接到哪个顶点，因此可以只将其连接到最近的顶点。由于只连接尚未连接的顶点，因此会得到一棵树，这就是你的算法。
然而，对于哈密顿路径，你确实关心将顶点 a 连接到哪个顶点（比如说 b），因为你不能再使用 b 了（否则它就不再是路径了）。因此，为了确定应该将 a 连接到哪个顶点，你必须尝试所有可能性并观察发生了什么。也就是说，目前还没有人找到有效的方法，当然这并不意味着不存在这样的方法。
- Matty
3
在哈密顿路径中，除源点和汇点外，所有顶点的度数都为2。但是在最小生成树（或者如果您需要的话，最小生成森林）中不一定是这样。
- nj-ath
2
汉密尔顿路径和特别是最小汉密尔顿循环对解决旅行商问题即寻找最短旅程非常有用。一种快速的解决方案看起来像希尔伯特曲线，一种特殊类型的空间填充曲线，也用于减少空间复杂度和有效地寻址。最小生成树类似于以最小成本连接（即旅行）所有顶点，而无论其顺序或交叉如何。 它可用于解决诸如查找道路、找到水渠、查找互联网电缆之类的问题。
- Micromega
0
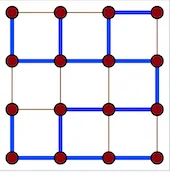
s到t的路径，也可能不是。图片中的生成树不是一条路径。
正如上面有人提到的，路径中的度数都是1或2。在上面的树中，你可以看到一些度数为3的顶点。
如果你对为什么没有已知的多项式时间算法来解决HAMPATH问题感兴趣，我推荐看一下Tim Roughgarden的书籍，第4部分。他称之为"MST vs. TSP: An Algorithmic Mystery"。
标准答案是HAMPATH是一个NP完全问题。这并不意味着没有多项式时间的算法，但这是最现实的情况。已知的这类问题的算法对于某些实例来说可能是相当合理的，只是不是多项式时间。
- irudyak
网页内容由stack overflow 提供, 点击上面的可以查看英文原文，
原文链接
原文链接