我有一个由邻接表表示的图,他的MST用parent数组表示。
我的问题是我需要从图中删除一条边并更新parent数组。
我已经成功处理了以下情况:
1.该边不存在; 2.该边在图中但不在MST中(MST不变); 3.该边是两个节点之间唯一的路径(在这种情况下,我返回null,因为图不连通)。
当边在MST中且在图中形成了一个环时,我该怎么办?我需要在O(n+m)复杂度下完成此操作。
我用红色书写边的成本。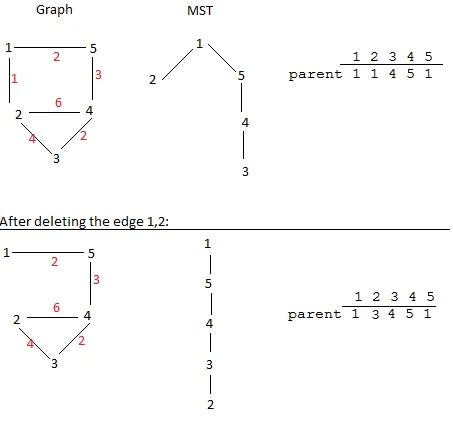
我的问题是我需要从图中删除一条边并更新parent数组。
我已经成功处理了以下情况:
1.该边不存在; 2.该边在图中但不在MST中(MST不变); 3.该边是两个节点之间唯一的路径(在这种情况下,我返回null,因为图不连通)。
当边在MST中且在图中形成了一个环时,我该怎么办?我需要在O(n+m)复杂度下完成此操作。
我用红色书写边的成本。

O(E)的。在寻找原始MST时,将边缘与MST中的属性标记为:e.mst = 1或0。删除MST边缘后,沿着从每个顶点开始的MST向外搜索,将每个顶点标记为拆分MST的“左半部分”或“右半部分”的一部分。每一侧需要O(E)。然后,对于所有边缘(u, v),如果u和v属于不同的MST半部分,则保留最小的这样的边缘并将其添加到MST中。 - brittohalloran