让我向您介绍一个有趣的数据结构,称为Wavelet Tree:
您可以通过查看整数的位串表示并递归地对其进行二分来构建它:
首先将整数分成具有最高有效位(MSB)0和具有MSB 1的两个子集。但是,您应该在位向量中以原始顺序存储MSBs。然后,对于这些整数的每个子集,您忽略MSB并递归地重复此构造以获取下一个最显著位。
如果您一直重复到最低有效位,您将得到以下树形结构(请注意,索引仅用于说明,您应该只存储位向量):
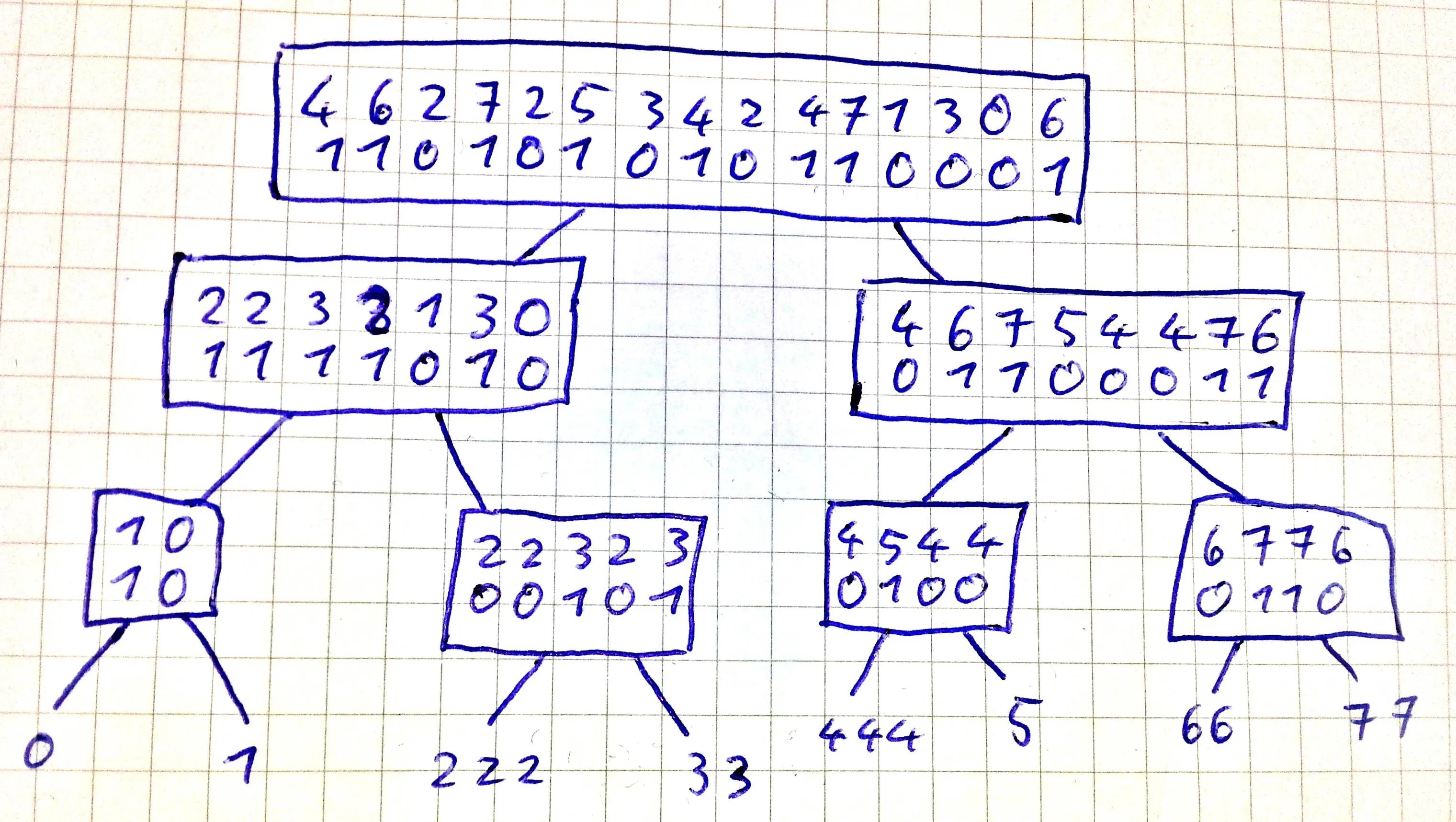
你可以轻松地看到,构建这个数据结构需要O(n log N)的时间,其中n是整数的数量,N是它们的最大值。
Wavelet树具有良好的特性,它们同时代表了原始序列和排序后的序列:
- 如果读取顶部的位向量,则可以获得输入序列的MSB。要重构条目的下一个位,可以在根节点的左子节点(如果MSB为0)或右子节点(如果MSB为1)中交替查找。对于以下位数,您可以继续递归。
- 如果从左到右读取叶节点,则可以得到排序后的序列。
要有效地使用Wavelet树,您需要对位向量执行两个基本操作:
- rank1(k)告诉你在位向量中第k个位置之前有多少个1,rank0同样适用于0
- select1(k)告诉你位向量中第k个1的索引,select0同样适用于0
请注意,有些位向量表示方法只需要额外存储o(n)(小o)比特即可在O(1)时间内实现这些操作
您可以按照以下方式利用它们:
现在,如何使用此实现 区间中位数查询?您需要进行的最重要的觉悟是,找到大小为k的范围的中位数等同于选择第k/2个元素。
该算法的基本思想类似于快速选择(Quickselect):将元素范围一分为二,并仅递归到包含所寻找元素的范围。
假设我们想找到从第二个2(包括)开始到1(不包括)结束的范围的中位数。
这些是7个元素,因此中位数在该范围内排名为4(第四小的元素)。
现在,在根比特向量的开头和结尾使用rank0/1调用,我们可以在根节点的子节点中找到相应的范围:
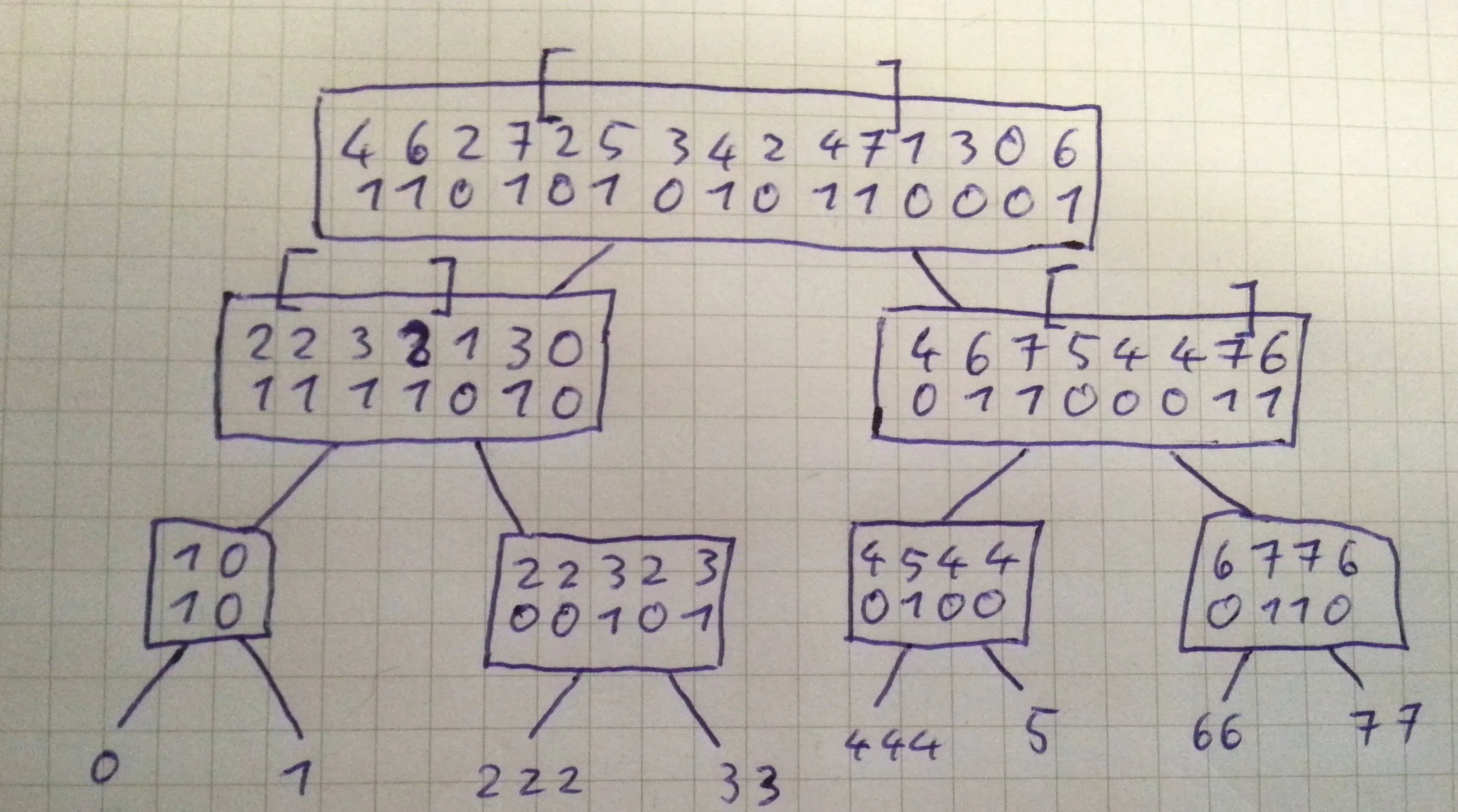
正如您所看到的,左范围(仅包含较小的元素)仅有3个元素,因此排名为4的元素必须包含在根节点的右子节点中。现在我们可以在右子节点中递归搜索排名为
4-3=1的元素。通过递归下降波束树直到达到叶子,您可以仅使用每个Wavelet树级别的两个排名操作(即O(1)时间)来识别中位数,因此整个范围中位数查询需要O(log N)时间,其中N是您输入序列中的最大数字。
如果您想查看这些Wavelet树的实际实现,请查看
Succinct Data Structures Library (SDSL),该库实现了上述位向量和不同的WT变体。

