在尝试了一些想法后,我提出了另一个解决方案,比我之前的答案更准确,可能更快,如果正确执行的话。然而,这相当复杂,需要相当多的数学,虽然不是非常复杂的数学。此外,这还在进行中:我仍在研究一些领域。尽管如此,从我所尝试的来看,它已经产生了非常好的结果。
问题
定义和目标
在本答案中,“p [n]”指第n个点的位置,“v [n]”指其速度,“a [n]”指其加速度,“j [n]”指其急加速度(加速度的导数)。第n个点的速度仅取决于其位置和上一个点的位置。同样对于加速度和急加速度,但是分别使用点的速度和加速度。
我们有起点和终点,分别为
p[0]和
p[n],它们都带有关联速度
v[0]和
v[n]。目标是在它们之间放置
n-1个点,其中
n是任意的,使得在X、Y和Z轴上,这些点(以及
p[n])的加速度和极限值分别低于一些限制,分别为加速度的
aMaxX、
aMaxY和
aMaxZ,以及抖动的
jMaxX、
jMaxY和
jMaxZ的绝对值。
我们想要找到所有
i∈[1; n-1]的
p[i]的值。因为
p[i] = p[i-1] + v[i],所以这等同于找到
v[i]。同样的推理,有
v[i] = v[i-1] + a[i]和
a[i] = a[i-1] + j[i],这也等同于找到
a[i]或
j[i]。
a[0]和a[n+1]被假定为零。
观察和简化
由于问题的限制与维度无关,我们可以分别解决每个维度的问题,只要在每种情况下获得的点数相同。因此,我只会使用aMax和jMax来解决问题的一维版本,而不考虑轴。
* [WIP] * 确定要先解决的最坏情况,然后解决其他情况,知道点数。
这两个给定点的实际位置并不重要,重要的是它们之间的相对距离,我们可以将其定义为 P = p[n] - p[0]。同时,让我们定义区间为R = [1; n]和R* = [1; n+1]。
由于问题的离散性质,我们可以得到以下等式。请注意,∑{i∈R}(x[i])是所有i∈R的x[i]的总和。
Ⓐ ∑{i∈R}(v[i]) = P
Ⓑ ∑{i∈R}(a[i]) = v[n] - v[0]
Ⓧ ∑{i∈R*}(j[i]) = 0
Ⓧ源于假设a[0] = a[n+1] = 0。
通过Ⓐ和v[i] = v[i-1] + a[i], i∈R,我们可以推断:
Ⓒ ∑{i∈R}((n+1-i)*a[i]) = P - n*v[0]
通过同样的逻辑,从 Ⓑ、Ⓒ 和
a[i] = a[i-1] + j[i], i∈R,我们可以推断出:
Ⓨ ∑{i∈R}((n+1-i)*j[i]) = v[n] - v[0]
Ⓩ ∑{i∈R}(T[n+1-i]*j[i]) = P - n*v[0]
在此,
T[n]是第n个三角形数,由
T[n] = n*(n+1)/2定义。
方程式 Ⓧ、Ⓨ和Ⓩ是接下来部分的相关方程式。
方法:
为了将
n最小化,我们可以从一个较小的值(1、2?)开始寻找解决方案。然后,如果
max{i∈R}(abs(a[i])) > aMax或
max{i∈R}(abs(j[i])) > jMax,我们可以递增
n并重复这个过程。
* [WIP] * 查找
n的下限,以避免从较小的
n值进行不必要的计算。或者估算正确的
n值,并通过测试解决方案来确定它。
寻找解决方案需要找到所有
i∈R*的
j[i]的值。我尚未找到
j[i]的最佳形式,但定义
j*[i]、
r[i]和
s[i],使得
j[i] = j*[i] + r[i]v[0] + s[i]v[n]效果很好。
*[WIP]* 寻找更好的j[i]形式
通过这样做,我们将n-1个未知数(j[i], i∈R, 注意j[n+1] = -∑{i∈R}(j[i]))转化为3(n-1)个更易于找到的未知数。现在,我们可以从Ⓧ、Ⓨ和Ⓩ中推断出一些东西。
∑{i∈R*}(r[i]) = 0
∑{i∈R*}(s[i]) = 0
∑{i∈R}((n+1-i)*r[i]) = -1
∑{i∈R}((n+1-i)*s[i]) = 1
∑{i∈R}(T(n+1-i)*r[i]) = -n
∑{i∈R}(T(n+1-i)*s[i]) = 0
作为提醒,这里有Ⓧ、Ⓨ和Ⓩ。
Ⓧ ∑{i∈R*}(j[i]) + j[n+1] = 0
Ⓨ ∑{i∈R}((n+1-i)*j[i]) = v[n] - v[0]
Ⓩ ∑{i∈R}(T[n+1-i]*j[i]) = P - n*v[0]
现在的目标是找到足够的特殊情况来帮助我们确定这些未知数。
特殊情况
v[0] = v[n] = 0
通过尝试不同的加速度值,我发现将j[i], i∈R*全部作为抛物线的一部分可以极大地减少加速度和加加速度。虽然这不是最佳拟合,但我还没有找到更好的方法。
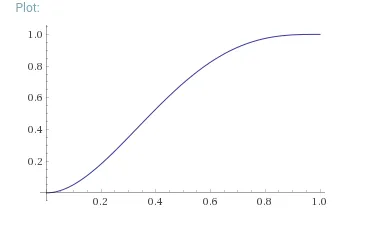
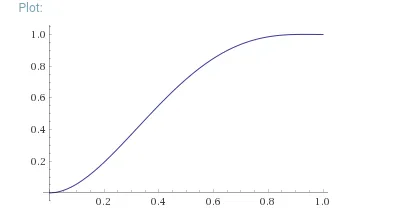
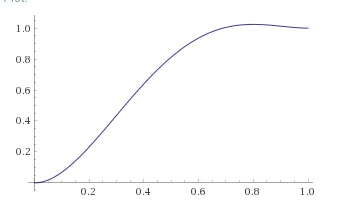
把加速度值看作抛物线的直觉是,如果位置的值要遵循一个多项式,那么它的次数必须至少为5,可以是5。如果你考虑速度值遵循一个4次多项式的情况,这会更容易理解。设置了v[0]和v[n]的约束条件,以及a[0] = a[n+1] = 0,并且它在[0; n]上的积分必须等于P,这个多项式必须至少有4次。这适用于连续和离散的情况。最后,似乎选择最小的次数可以使加速度更平稳,并且更容易计算。
这是一个连续案例的示例,其中位置用紫色表示,速度用蓝色表示,加速度用黄色表示,而加加速度则用红色表示。
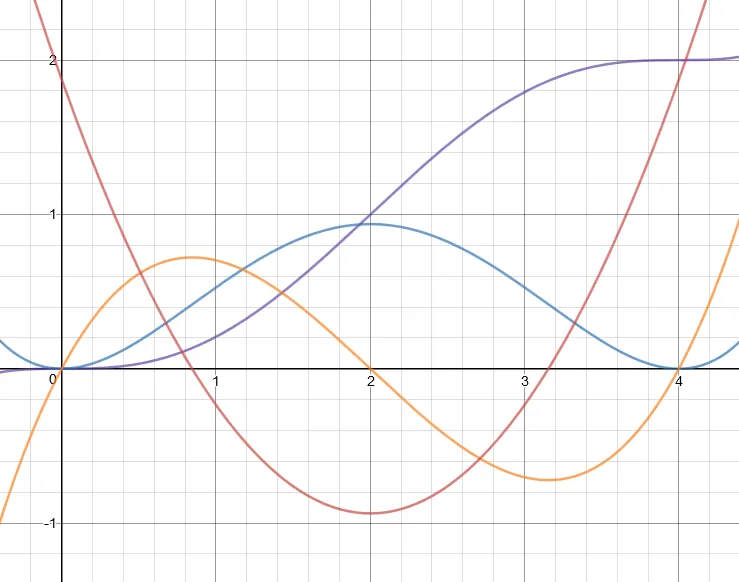
如果您想尝试一下,以下是如何根据
n,
p[0],
p[n],
v[0]和
v[n](其他的只是导数)来定义位置曲线。
a = (-3(v[n]+v[0]) + 6(p[n]-p[0])) / n^5
b = (n(7v[n]+8v[0]) - 15(p[n]-p[0])) / n^4
c = (-n(4v[n]+6v[0]) + 10(p[n]-p[0])) / n^3
p[x] = ax^5 + bx^4 + cx^3 + v[0]x + p[0]
如果
v[0] = v[n] = 0,那么
j[i] = j*[i], i∈R*。这意味着
j*[i]的值遵循二次多项式。因此,我们想要找到
α、
β和
γ,使得Ⓟ成立。
Ⓟ j*[i] = αi^2 + βi + γ, i∈R*
从 Ⓧ、Ⓨ 和 Ⓩ 中,按照以下方程式。
α*∑{i∈R*}(i^2) + β*∑{i∈R*}(i) + c*∑{i∈R*}(1) = 0
α*∑{i∈R}((n+1-i)*i^2) + β*∑{i∈R}((n+1-i)*i) + c*∑{i∈R}(n+1-i) = 0
α*∑{i∈R}(T(n+1-i)*i^2) + β*∑{i∈R}(T(n+1-i)*i) + c*∑{i∈R}(T(n+1-i)) = P
解决这个系统可以得到
α、
β 和
γ,它们可以与 Ⓟ 一起用于计算
j*[i], i∈R*。请注意,
j*[i] = j*[n+2-i],因此只需要完成计算的上半部分。
如果
v[0] = v[n] = 1/n,那么
j[i] = 0, i∈R*。这意味着 Ⓠ 成立。
Ⓠ r[i] + s[i] = -n*j[i], i∈R*
v[0] = 0, j[i∈L] = J, j[h] = 0, j[i∈U] = -J
L和U分别是R*的下半部分和上半部分,如果n+1为奇数,则h为中间值。换句话说:
if n is odd:
L = [1
U = [(n+3)/2
if n is even:
L = [1
h = n/2+1
U = [n/2+2
这种特殊情况对应于在最小化
abs(j[i]), i∈R*的同时,
p[0]和
p[n]之间的最大总加速度。 在这里,Ⓩ给出了以下方程式。
∑{i∈R}(T[n+1-i]*j[i]) = P
∑{i∈L}(T[n+1-i])*j[1] + ∑{i∈U}(T[n+1-i])*j[n+1] = P
j[1] = P / [ ∑{i∈L}(T[n+1-i]) - ∑{i∈U}(T[n+1-i]) ]
这给出了j[1],因此对于每个j[i],i∈R*都是如此。然后我们可以使用Ⓨ计算v[n]。
将各个部分组合在一起
每个特殊情况都为某些v[0],v[n]和P的值提供了一个形式为
αj*[i] + βr[i] + γs[i] = δ的关系。
通过处理三种特殊情况(假设它们不相似,即它们不会给出相同的关系),我们得到了一个包含三个方程的系统,一旦解决,就可以为所有i∈R*的j*[i],r[i]和s[i]的值提供解决方案。
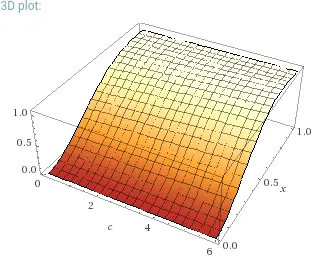
作为结果,我们可以针对每个
n的值计算
j[i]的值,这取决于
v[0],
v[n]和
P。它们可以预先计算,这意味着对于任何
n的值进行测试都可以非常快速地完成。因此,只要我们预先计算了到足够大的
n值的值,我们就可以非常快速地找到轨迹所需的最少点数的良好估计,以及最佳轨迹的良好近似。
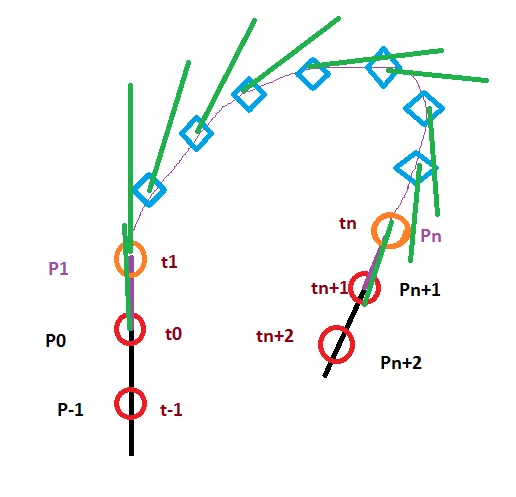

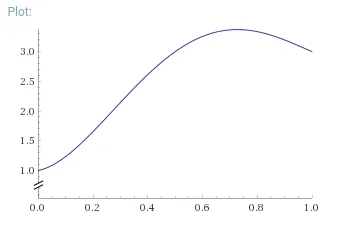
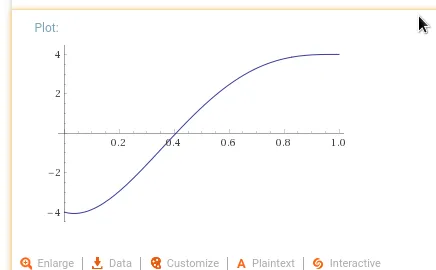

Pn? - meowgoesthedog