我很难确定欧几里得算法的时间复杂度。这个伪代码如下：
function gcd(a, b)
while b ≠ 0
t := b
b := a mod b
a := t
return a
看起来这取决于a和b。我认为时间复杂度为O(a%b)。这正确吗？有更好的写法吗？
欧几里得算法的时间复杂度
119
- Donald T
2
11个回答
87
分析欧几里得算法时间复杂度的一个技巧是观察两次迭代之间发生了什么：
a', b' := a % b, b % (a % b)
现在a和b都会减少，而不是只有其中一个，这使得分析更容易。您可以将其分为以下情况：
- 极小的A：
2a <= b - 极小的B：
2b <= a - 较小的A：
2a > b但a < b - 较小的B：
2b > a但b < a - 相等：
a == b
现在我们将展示每种情况如何使总和a+b减少至少四分之一：
- 极小的A：由于
2a <= b且b % (a % b) < a，因此b至少减少一半，所以a+b至少减少25% - 极小的B：由于
2b <= a且a % b < b，因此a至少减少一半，所以a+b至少减少25% - 较小的A：
b将变为b-a，小于b/2，使a+b至少减少25%。 - 较小的B：
a将变为a-b，小于a/2，使a+b至少减少25%。 - 相等：
a+b降至0，显然会将a+b至少减少25%。
因此，通过案例分析，每个双步都会将a+b至少减少25%。在a+b强制降至1之前，最多可以发生这种情况的次数是有限的。直到我们达到0的总步数（S）必须满足(4/3)^S <= A+B。现在就开始计算：
(4/3)^S <= A+B
S <= lg[4/3](A+B)
S is O(lg[4/3](A+B))
S is O(lg(A+B))
S is O(lg(A*B)) //because A*B asymptotically greater than A+B
S is O(lg(A)+lg(B))
//Input size N is lg(A) + lg(B)
S is O(N)
因此，迭代次数与输入数字的位数成线性关系。对于适合放入CPU寄存器中的数字，可以合理地将迭代模拟为花费恒定时间，并假装gcd的总运行时间是线性的。
当然，如果您处理的是大整数，则必须考虑每次迭代中的模数运算不具有恒定的成本。粗略地说，总渐进运行时间将是n^2乘以一个多对数因子。类似于n^2 lg(n) 2^O(log* n)之类的东西。可以通过使用二进制GCD算法来避免多对数因子。
- Craig Gidney
9
你能解释一下为什么 "b % (a % b) < a" 吗？ - Michael Heidelberg
4
x % y 的值不能大于 x，必须小于 y。因此，a % b 最大只能是 a，这强制 b % (a%b) 的值低于不超过 a 的某个值，因此总体上要比 a 小。 - Craig Gidney@Cheersandhth.-Alf，您认为术语上的轻微差异就是“严重错误”吗？当然我使用了计算机科学的术语；这是一个计算机科学问题。无论如何，我澄清了答案，说“数字的数量”。 - Craig Gidney
@CraigGidney：感谢您修复了那个问题。现在我认识到了许多由纯学者撰写的维基百科文章中存在的沟通问题。请考虑这一点：谈论数字位数的主要原因，而不仅仅是像我在评论中所做的那样写成O(log(min(a,b)))，是为了使非数学专业人士更容易理解。如果没有这方面的考虑，只需写“log”等即可。因此，数字位数的目的是帮助那些有挑战性的人。当您将这个概念命名为“大小”，并在其他地方定义它，并且不在最后谈论“log”时，您会使事情变得更加模糊，而不是有所帮助。 - Cheers and hth. - Alf
@Robur_131 33% 的减少意味着至少减少了25%。有什么问题吗？ - Craig Gidney
显示剩余4条评论
32
分析算法的适当方法是确定其最坏情况。欧几里得GCD的最坏情况发生在涉及斐波那契对的情况下，其中 i > 0，
例如，让我们选择被除数为55，除数为34（请记住我们仍在处理斐波那契数）。
正如您所看到的，这个操作花费了8次迭代（或递归调用）。
让我们尝试更大的Fibonacci数字，即121393和75025。同样，我们也可以注意到它需要24次迭代（或递归调用）。
您还可以注意到每次迭代产生一个斐波那契数。那就是为什么有这么多操作。实际上，我们不能只用斐波那契数获得类似的结果。
因此，时间复杂度将由小Oh（上限）表示。这次，下限直观上是Omega（1）：比如500除以2的情况。
让我们解决递归关系：
然后我们可以说，欧几里得GCD最多可以进行log(xy)次操作。
void EGCD(fib[i], fib[i - 1])。例如，让我们选择被除数为55，除数为34（请记住我们仍在处理斐波那契数）。
正如您所看到的，这个操作花费了8次迭代（或递归调用）。
让我们尝试更大的Fibonacci数字，即121393和75025。同样，我们也可以注意到它需要24次迭代（或递归调用）。
您还可以注意到每次迭代产生一个斐波那契数。那就是为什么有这么多操作。实际上，我们不能只用斐波那契数获得类似的结果。
因此，时间复杂度将由小Oh（上限）表示。这次，下限直观上是Omega（1）：比如500除以2的情况。
让我们解决递归关系：
然后我们可以说，欧几里得GCD最多可以进行log(xy)次操作。
- Mohamed Ennahdi El Idrissi
3
3我认为这份分析是错误的，因为基础取决于输入。 - HopefullyHelpful
你能证明依赖基表示了一个问题吗？ - Mohamed Ennahdi El Idrissi
1基数显然是黄金比例。为什么？因为计算nod(13,8)与nod(8,5)需要正好多一步。对于固定的x，如果y<x，则最坏情况下的性能为x=fib(n+1)，y=fib(n)。这里y取决于x，所以我们只需考虑x。 - Stepan
19
在维基百科文章上有很好的介绍。
它甚至还提供了值对复杂性的漂亮图表。
它不是O(a%b)。
众所周知（请参见文章），它所需的步骤数永远不会超过较小数字的位数的五倍。因此，步骤的最大数量随着数字位数的增加而增长(ln b)。每个步骤的成本也随着数字位数的增加而增长，因此其复杂度受到O(ln^2 b)的限制，其中b是较小的数字。这是一个上限，实际时间通常更短。
- JoshD
5
@IVlad：数字位数。我已经澄清了答案，谢谢。 - JoshD
对于 OP 的算法，实际上是类似于 O(n^2 log^2n) 的东西，使用（大整数）除法而非减法。 - Alexandre C.
@Alexandre C.：记住
n = ln b。大数取模的常规复杂度是多少？它是 O(log n log^2 log n) 吗？ - JoshD@JoshD：大概就是这样，我想我错过了一个log n项，在这种情况下，使用除法的算法的最终复杂度为O（n ^ 2 log ^ 2 n log n）。 - Alexandre C.
@JoshD：我漏掉了一些东西：对于大整数的除法余数，典型的复杂度是O(n log^2 n log n)或O(n log^2n)或类似的（我不记得确切的数字），但肯定至少与位数成线性关系。 - Alexandre C.
16
- IVlad
1
4对于步骤的数量来说，这是正确的，但它并没有考虑到每个步骤本身的复杂性，这与数字的位数成比例增长（ln n）。 - JoshD
9
这里有一个对欧几里得算法运行复杂度的直观理解。正式证明在各种文本中都有涵盖，例如《算法导论》和《计算机程序设计艺术》第2卷。
首先考虑一下如果我们试图求两个斐波那契数F(k+1)和F(k)的最大公约数gcd。您可能很快就会发现欧几里得算法迭代到F(k)和F(k-1)。也就是说，每次迭代我们在斐波那契数列中向下移动一个数字。由于斐波那契数是O(Phi ^ k)，其中Phi是黄金比例，因此我们可以看出GCD的运行时间为O(log n)，其中n = max(a, b)，log的底数为Phi。接下来，我们可以通过观察到斐波那契数始终产生保持足够大的余数的配对，并且在每次迭代中从未变为零，直到到达系列开始，来证明这将是最坏情况。
我们可以使n = max(a, b)的O(log n)边界更加紧密。假设b >= a，因此我们可以将边界写为O(log b)。首先，观察到GCD(ka, kb) = GCD(a, b)。由于k的最大值是gcd(a,c)，因此我们可以将b替换为b / gcd(a,b)，从而导致更紧密的运行时间边界为O(log b / gcd(a,b))。
首先考虑一下如果我们试图求两个斐波那契数F(k+1)和F(k)的最大公约数gcd。您可能很快就会发现欧几里得算法迭代到F(k)和F(k-1)。也就是说，每次迭代我们在斐波那契数列中向下移动一个数字。由于斐波那契数是O(Phi ^ k)，其中Phi是黄金比例，因此我们可以看出GCD的运行时间为O(log n)，其中n = max(a, b)，log的底数为Phi。接下来，我们可以通过观察到斐波那契数始终产生保持足够大的余数的配对，并且在每次迭代中从未变为零，直到到达系列开始，来证明这将是最坏情况。
我们可以使n = max(a, b)的O(log n)边界更加紧密。假设b >= a，因此我们可以将边界写为O(log b)。首先，观察到GCD(ka, kb) = GCD(a, b)。由于k的最大值是gcd(a,c)，因此我们可以将b替换为b / gcd(a,b)，从而导致更紧密的运行时间边界为O(log b / gcd(a,b))。
- Shital Shah
1
你能否给出一个正式的证明，证明斐波那契数列产生欧几里得算法的最坏情况？ - Akash
6
以下是《C语言数据结构与算法分析》（第二版，2.4.4）一书中的分析：
欧几里得算法通过不断计算余数直到达到0来工作，最后一个非零余数就是答案。
以下是代码：
unsigned int Gcd(unsigned int M, unsigned int N)
{
unsigned int Rem;
while (N > 0) {
Rem = M % N;
M = N;
N = Rem;
}
Return M;
}
这里有一个我们将要使用的定理：
如果 M > N，那么 M mod N < M/2。
证明：
有两种情况。如果N <= M/2，则由于余数小于N，此情况下定理成立。另一种情况是N > M/2。但是，N除M有余数 M - N < M/2，证明了该定理。
因此，我们可以得出以下推论：
Variables M N Rem
initial M N M%N
1 iteration N M%N N%(M%N)
2 iterations M%N N%(M%N) (M%N)%(N%(M%N)) < (M%N)/2
所以，经过两次迭代后，余数最多是原始值的一半。这表明迭代次数至多为
2logN = O(logN)。请注意，该算法计算Gcd（M，N），假设M>= N。（如果N> M，则循环的第一次迭代会交换它们。）
- cd-00
5
当n和m都是连续的斐波那契数时，最坏情况将会出现。
gcd(Fn,Fn−1)=gcd(Fn−1,Fn−2)=⋯=gcd(F1,F0)=1，第n个斐波那契数是1.618^n，其中1.618是黄金比例。
因此，要找到gcd(n,m)，递归调用的次数将为Θ(logn)。
- Arnav Attri
4
欧几里得算法的最坏情况是每步余数都取最大值，即斐波那契数列的两个连续项。
当a和b的位数分别为n和m时，假设n >= m，则该算法使用O(m)次除法。
请注意，复杂度总是以输入的“大小”为单位给出，本例中为数字的位数。
- Alexandre C.
2
加布里埃尔·拉默定理限制了步数的数量为log(1/sqrt(5)*(a+1/2))-2，其中对数的底数为(1+sqrt(5))/2。这是算法最坏情况下的情形，并且当输入为连续的斐波那契数时发生。
稍微宽松一点的界限是：Koblitz暗示了以(sqrt(2))为底数的log a。
出于加密目的，我们通常考虑算法的位复杂度，考虑到位数大约由k=loga给出。
以下是欧几里得算法的位复杂度的详细分析：
尽管在大多数参考文献中，欧几里得算法的位复杂度为O(loga)^3，但存在一个更紧密的界限，即O(loga)^2。
考虑; r0=a, r1=b, r0=q1.r1+r2 . . . ,ri-1=qi.ri+ri+1, . . . ,rm-2=qm-1.rm-1+rm rm-1=qm.rm
观察到：a=r0>=b=r1>r2>r3...>rm-1>rm>0 ..........(1)
而rm是a和b的最大公约数。
通过Koblitz书中的一个声明可以证明：ri+1<(ri-1)/2 .................(2)
再次在Koblitz中，将k位正整数除以l位正整数所需的位操作数（假设k>=l）为：(k-l+1).l ...................(3)
由(1)和(2)可知，除法的次数为O(loga)，因此根据(3)，总复杂度为O(loga)^3。
现在可以通过Koblitz的一条备注将其减少到O(loga)^2。
考虑ki= logri +1
由(1)和(2)我们有：ki+1<=ki for i=0,1,...,m-2,m-1 and ki+2<=(ki)-1 for i=0,1,...,m-2
并且由(3)，m个除法的总成本受限于：SUM [(ki-1)-((ki)-1))]*ki for i=0,1,2,..,m
重新排列这个式子：SUM [(ki-1)-((ki)-1))]*ki<=4*k0^2
因此，欧几里得算法的位复杂度为O(loga)^2。
稍微宽松一点的界限是：Koblitz暗示了以(sqrt(2))为底数的log a。
出于加密目的，我们通常考虑算法的位复杂度，考虑到位数大约由k=loga给出。
以下是欧几里得算法的位复杂度的详细分析：
尽管在大多数参考文献中，欧几里得算法的位复杂度为O(loga)^3，但存在一个更紧密的界限，即O(loga)^2。
考虑; r0=a, r1=b, r0=q1.r1+r2 . . . ,ri-1=qi.ri+ri+1, . . . ,rm-2=qm-1.rm-1+rm rm-1=qm.rm
观察到：a=r0>=b=r1>r2>r3...>rm-1>rm>0 ..........(1)
而rm是a和b的最大公约数。
通过Koblitz书中的一个声明可以证明：ri+1<(ri-1)/2 .................(2)
再次在Koblitz中，将k位正整数除以l位正整数所需的位操作数（假设k>=l）为：(k-l+1).l ...................(3)
由(1)和(2)可知，除法的次数为O(loga)，因此根据(3)，总复杂度为O(loga)^3。
现在可以通过Koblitz的一条备注将其减少到O(loga)^2。
考虑ki= logri +1
由(1)和(2)我们有：ki+1<=ki for i=0,1,...,m-2,m-1 and ki+2<=(ki)-1 for i=0,1,...,m-2
并且由(3)，m个除法的总成本受限于：SUM [(ki-1)-((ki)-1))]*ki for i=0,1,2,..,m
重新排列这个式子：SUM [(ki-1)-((ki)-1))]*ki<=4*k0^2
因此，欧几里得算法的位复杂度为O(loga)^2。
- esra
1
对于迭代算法，我们有以下内容：
根据Dr. Jauhar Ali的工作（最后一张幻灯片），上述循环是对数的。
int iterativeEGCD(long long n, long long m) {
long long a;
int numberOfIterations = 0;
while ( n != 0 ) {
a = m;
m = n;
n = a % n;
numberOfIterations ++;
}
printf("\nIterative GCD iterated %d times.", numberOfIterations);
return m;
}
使用斐波那契对，iterativeEGCD()和iterativeEGCDForWorstCase()之间没有区别，其中后者如下所示：
int iterativeEGCDForWorstCase(long long n, long long m) {
long long a;
int numberOfIterations = 0;
while ( n != 0 ) {
a = m;
m = n;
n = a - n;
numberOfIterations ++;
}
printf("\nIterative GCD iterated %d times.", numberOfIterations);
return m;
}
是的，使用斐波那契数对，n = a % n 和 n = a - n 是完全相同的。
我们还知道，在先前回答同一问题时，有一个主导的递减因子：factor = m / (n % m)。
因此，为了将欧几里得算法的迭代版本形成一个定义良好的形式，我们可以将其描绘成一个像这样的“模拟器”：
void iterativeGCDSimulator(long long x, long long y) {
long long i;
double factor = x / (double)(x % y);
int numberOfIterations = 0;
for ( i = x * y ; i >= 1 ; i = i / factor) {
numberOfIterations ++;
}
printf("\nIterative GCD Simulator iterated %d times.", numberOfIterations);
}
根据Dr. Jauhar Ali的工作（最后一张幻灯片），上述循环是对数的。
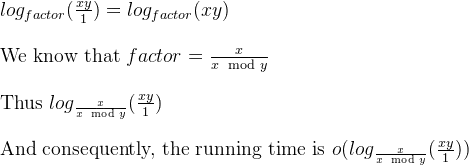
是的，小Oh因为模拟器告诉了迭代次数最多。当在欧几里得GCD上探测非斐波那契对时，所需的迭代次数比斐波那契对要少。
- Mohamed Ennahdi El Idrissi
1
由于本研究采用C语言进行，精度问题可能会导致错误/不精确的值。这就是为什么使用“long long”更适合名为“factor”的浮点变量。
所使用的编译器是MinGW 2.95。 - Mohamed Ennahdi El Idrissi
网页内容由stack overflow 提供, 点击上面的可以查看英文原文，
原文链接
原文链接
a%b不成比例。最坏情况是当a和b是相邻的斐波那契数时。 - Jerry Coffin