寻找一个二进制数中2的次幂位置上为1的索引

Question

假设我有一个数x，它是2的幂次方，也就是说x = 2^i (i为整数)。 那么x的二进制表示中只有一个'1'。我需要找到那个'1'的下标。 例如，x = 16 (十进制) x = 10000 (二进制) 这里的下标应该是4。通过位运算在O(1)时间内是否能找到下标呢？

- Shadekur Rahman

---

log_2(x)（5个字符） - amit

“仅使用位运算，能否在O(1)时间内找到索引？” 如果您假设整数中有固定数量的位，则朴素方法（通过除以2进行迭代）是常数时间。否则，由于输出为“log(n)”，并且您需要“log(log(n))”位来编写此数字 - 不，它无法在常数时间内完成。也许您的意思是亚对数时间？ - amit

在一个64位IEEE浮点数中找到一个整数的以2为底的对数 - 随便选一个链接。 - Andrew Morton

@FilipeGonçalves 如果你可以使用O(1)表查找完成它，那么你也可以使用O(1)算术运算完成它，因为显然你有O(1)位，所以甚至没有一个“n”需要担心。 - harold

哈希表或查找表，你说它很可能是O(1)操作。但实现起来很困难。 - Shadekur Rahman

Answer 1

以下是关于在@Juan Lopez和@njuffa提供的O(1)代码中使用de Bruijn序列逻辑的解释（顺便说一句，这些都是很好的答案，你应该考虑点赞）。

de Bruijn序列

给定字母表K和长度n，de Bruijn序列是一个由来自K的字符组成的序列，在其中包含了所有长度为n的排列（没有特定的顺序）[1]。例如，给定字母表{a，b}和n= 3，以下是{a，b}长度为3的所有排列（带重复）的列表：

 [aaa, aab, aba, abb, baa, bab, bba, bbb]

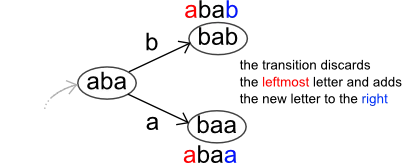
为了创建关联的de Bruijn序列，我们构建一个最小的字符串，其中包含所有这些排列而没有重复，其中一种这样的字符串是：babbbaaa。

"B(2, 3)" 表示我们的字母表 K = {a, b} 和 n = 3 的 de Bruijn 序列是 "babbbaaa"，其中 2 是 K 的大小，也表示为 k。序列的大小由 kⁿ 给出，在上面的例子中，kⁿ = 2³ = 8。 如何构建这样的字符串？一种方法是构建一个有向图，其中每个节点表示一个排列，并对字母表中的每个字母有一个出边，从一个节点到另一个节点的转换将边缘字母添加到下一个节点的右侧并删除其最左边的字母。构建完图后，在其上抓取 Hamiltonian path 上的边以构建序列。

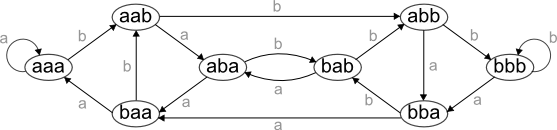
前面示例的图表如下：

然后，取一个哈密顿路径（即访问每个顶点恰好一次的路径）：

从节点 aaa 开始，沿着每条边走，我们最终得到:

(aaa) -> b -> a -> b -> b -> b -> a -> a -> a (aaa) = babbbaaa

我们可以从节点bbb开始，这样得到的序列将是“aaababbb”。

现在讲解了de Bruijn序列，让我们使用它来找到一个整数的前导零的数量。

de Bruijn算法[2]

为了找出一个整数值的前导零的数量，在该算法中的第一步是从右到左隔离第一个位，例如，给定848（1101010000₂）：

              isolate rightmost bit     
1101010000 ---------------------------> 0000010000

一种方法是使用x&（~x + 1），您可以在 Hacker's Delight book（第2章第2-1节）中找到有关此表达式如何工作的更多信息。

问题说明输入是2的幂次方，因此从一开始就隔离了最右边的位，因此不需要做任何努力。

一旦位被隔离（因此将其转换为2的幂次方），第二步就是使用哈希表方法以及其哈希函数将过滤后的输入映射到其相应的前导0的数量，例如，将哈希函数h（x）应用于0000010000₂应返回包含值4的表中的索引。

该算法提出使用完美哈希函数，强调以下属性：

• 哈希表应该很小
• 哈希函数应该易于计算
• 哈希函数不应产生冲突，即如果 x ≠ y，则 h(x) ≠ h(y)

为了实现这一点，我们可以使用 de Bruijn 序列，其中二进制元素的字母表为 K = {0, 1}，如果我们要解决 64 位整数的问题，则 n = 6（对于 64 位整数，有 64 种可能的二的幂值，需要 6 个位来计数所有这些值）。B(2, 6) = 64，因此我们需要找到一个长度为 64 的 de Bruijn 序列，其中包括长度为 6 的二进制数字的所有排列（000000₂，000001₂，...，111111₂）。

使用像上面描述的方法实现的程序，您可以生成满足 64 位整数要求的 de Bruijn 序列：

0000011111101101110101011110010110011010010011100010100011000010₂ = 7EDD5E59A4E28C2₁₆

该算法的建议哈希函数为：

h(x) = (x * deBruijn) >> (k^n - n)

其中x是2的幂。对于64位中所有可能的2的幂，h(x)返回相应的二进制排列，我们需要将每个排列与填充表格所需的前导零数关联起来。例如，如果x是16 = 10000₂，它有4个前导零，我们有：

h(16) = (16 * 0x7EDD5E59A4E28C2) >> 58
      = 9141566557743385632 >> 58
      = 31 (011111b)

因此，在我们的表格中，索引为31的位置存储了4。另一个例子，让我们处理256 = 100000000₂，它有8个前导零：

h(256) = (256 * 0x7EDD5E59A4E28C2) >> 58
       = 17137856407927308800 (due to overflow) >> 58
       = 59 (111011b)

在索引59处，我们存储8。我们重复这个过程直到填满表格的每一个2的幂次方。手动生成表格很麻烦，你应该使用一个程序像这里找到的那样来完成这个任务。

最后，我们将得到以下表格：

int table[] = {
      63,  0, 58,  1, 59, 47, 53,  2, 
      60, 39, 48, 27, 54, 33, 42,  3,
      61, 51, 37, 40, 49, 18, 28, 20,
      55, 30, 34, 11, 43, 14, 22,  4,
      62, 57, 46, 52, 38, 26, 32, 41,
      50, 36, 17, 19, 29, 10, 13, 21,
      56, 45, 25, 31, 35, 16,  9, 12,
      44, 24, 15,  8, 23,  7,  6,  5
};

计算所需值的代码：

// Assumes that x is a power of two
int numLeadingZeroes(uint64_t x) { 
    return table[(x * 0x7EDD5E59A4E28C2ull) >> 58];
}

如何保证由于碰撞而导致错过2的幂次方索引的情况不会发生？

哈希函数基本上获取每个2的幂次方包含在de Bruijn序列中的每个6位排列，乘以x 基本上只是向左移位（将一个数乘以2的幂次方等同于左移该数字），然后应用右移58，逐个隔离6位组，对于两个不同的x值不会出现碰撞（这个问题的期望哈希函数的第三个属性）由于de Bruijn序列。

---

参考资料：

[1] 德布鲁因序列 - http://datagenetics.com/blog/october22013/index.html

[2] 使用德布鲁因序列在计算机字中索引1 - http://supertech.csail.mit.edu/papers/debruijn.pdf

[3] 魔术位扫描 - http://elemarjr.net/2011/01/09/the-magic-bitscan/

- higuaro

---

在我看来，这是最佳答案。我觉得特别有趣的是，参考文献[3]是我的一个朋友写的，他受到启发写了这篇文章，因为我们正在编写一个国际象棋引擎，而我使用德布鲁因序列编写了这段代码来实现LSB。 :) - Juan Lopes

@JuanLopes 谢谢！是的，我在他的文章中看到了对 @juanlopes 的提及，说 7EDD5E59A4E28C2 是你最喜欢的数字 XD，非常棒的文章，尽管由于我的葡萄牙语水平不佳和一些谷歌翻译问题，阅读起来有点困难。 - higuaro

Answer 2

这取决于您的定义。首先，假设有n位，因为如果我们假设有恒定数量的位，则我们可能会用它们做的所有事情都需要恒定时间，因此我们无法进行比较。

首先，让我们尽可能广泛地看待“按位运算”-它们操作位，但不一定是逐点的，并且此外，我们将计算操作次数，而不包括操作本身的复杂性。

M.L. Fredman和D.E. Willard表明，存在一种O（1）操作算法来计算lambda（x）（x的以2为底的对数的底部，因此是最高设置位的索引）。它包含相当多的乘法，因此称其为按位有些滑稽。

另一方面，有一个明显的O（log n）操作算法，不使用任何乘法，只需进行二进制搜索即可找到它。但可以做得更好，Gerth Brodal表明，它可以在O（log log n）个操作中完成（其中没有乘法）。

我提到的所有算法都在《计算机程序设计艺术》4A，按位技巧和技术中。

这些算法都不能真正符合在常量时间内找到1的要求，显然你无法做到这一点。其他答案也不符合要求，尽管它们声称可以。它们很酷，但它们是针对特定的常量位数设计的，因此任何简单算法也将是O（1）（显然，因为没有n依赖）。在评论中，OP说了一些暗示他实际上想要的东西，但从技术上讲，这并没有回答问题。

- harold

---

标准的位运算随着固定字大小（即线性单词数）中的任意位数线性扩展，如加法、减法等也是如此。但是对于具有固定字大小的任意n位的乘法，更像是O（nlogn）。即使这样做，使用快速FFT等方法来避免O(n ^ 2)也相当混乱。因此，对于任意n，你提到的解决方案，它使用了O（log log n）位运算而没有使用乘法，似乎是可行的。你能简要概述或提示这种方法是如何工作的吗？并且它是否真正适用于比字大小更大的位数？ - user2566092

@user2566092，这并不重要，对于这个问题来说，它也是无限宽度的位运算计数。如果你回到RAM机器上，那么所有这些都无关紧要，找到那个1最快的方法就是线性扫描。 - harold

基本上，它通过丢弃一些2的幂来计算结果的高位数（这类似于对lambda(x)进行二进制搜索），然后滥用字的宽度以并行计算其余部分（由于第一步，字比正在处理的值宽得多，因此它可以在字中多次拟合以进行并行工作）。 - harold

@גלעד ברקן 不，它的常数因子比那个高得多。 - harold

@גלעד ברקן，这只是意味着它在渐近意义下具有良好的可扩展性，它并不保证确切的操作次数。 - harold

Answer 3

问题的规格对我来说不是完全清楚。例如，哪些操作被视为“位运算”，输入中有多少个位？许多处理器可以通过固有的“计算前导零”或“查找第一位”的指令来直接提供所需的结果。

下面展示了如何基于De Bruijn序列在32位整数中找到位位置。

#include <stdio.h>
#include <stdlib.h>
#include <stdint.h>

/* find position of 1-bit in a = 2^n, 0 <= n <= 31 */
int bit_pos (uint32_t a)
{
    static int tab[32] =  {  0,  1,  2,  6,  3, 11,  7, 16,  
                             4, 14, 12, 21,  8, 23, 17, 26, 
                            31,  5, 10, 15, 13, 20, 22, 25, 
                            30,  9, 19, 24, 29, 18, 28, 27};

    // return tab [0x04653adf * a >> 27];
    return tab [(a + (a <<  1) + (a <<  2) + (a <<  3) + (a <<  4) + (a <<  6) + 
                     (a <<  7) + (a <<  9) + (a << 11) + (a << 12) + (a << 13) +
                     (a << 16) + (a << 18) + (a << 21) + (a << 22) + (a << 26)) 
                >> 27];
}

int main (void)
{
    uint32_t nbr;
    int pos = 0;
    while (pos < 32) {
        nbr = 1U << pos;
        if (bit_pos (nbr) != pos) {
            printf ("!!!! error:  nbr=%08x  bit_pos=%d  pos=%d\n",
                    nbr, bit_pos(nbr), pos);
            EXIT_FAILURE;
        }
        pos++;
    }
    return EXIT_SUCCESS;
}

- njuffa

---

感谢njuffa的努力。实际上，20位对于我的情况已经足够了。但是它是否显示了所有2^i的位置，直到i = 20？对于某些2^i，则会显示为0。 - Shadekur Rahman

@ShadekurRahman 如果20位足够了，那你为什么还要问理论结果呢？直接选择现实生活中最快的解决方案（即bitscan内在函数）就好了。 - harold

@ShadekurRahman 不确定你的意思。我的答案提供了一个测试框架，用于测试 bit_pos() 在 i=0,..31 时的 2**i。我使用两个不同的编译器编译了代码，并且测试通过。你在哪个值上看到 bit_pos() 返回了错误的结果？ - njuffa

Answer 4

如果您允许单次内存访问，您可以在 O(1) 时间复杂度内完成此操作：

#include <iostream>
using namespace std;

int indexes[] = {
    63, 0, 58, 1, 59, 47, 53, 2,
    60, 39, 48, 27, 54, 33, 42, 3,
    61, 51, 37, 40, 49, 18, 28, 20,
    55, 30, 34, 11, 43, 14, 22, 4,
    62, 57, 46, 52, 38, 26, 32, 41,
    50, 36, 17, 19, 29, 10, 13, 21,
    56, 45, 25, 31, 35, 16, 9, 12,
    44, 24, 15, 8, 23, 7, 6, 5
};

int main() {
    unsigned long long n;
    while(cin >> n) {
        cout << indexes[((n & (~n + 1)) * 0x07EDD5E59A4E28C2ull) >> 58] << endl;
    }
}

- Juan Lopes

---

它非常快。你能告诉我背后的基本逻辑是什么吗？ - Shadekur Rahman

不需要 n & (~n + 1)，因为问题已经保证只有一个位被设置。 - harold

@ShadekurRahman，我发表了一个答案，试图解释这个神奇算法背后的逻辑。 - higuaro

Answer 5

答案是......是的！

仅出于娱乐目的，因为您在其中一个答案下面评论说 i 最多到 20 就足够了。

（这里的乘法只有 0 或 1 的情况）

#include <iostream>
using namespace std;

int f(int n){
 return 
   0 | !(n ^ 1048576) * 20
     | !(n ^ 524288) * 19
     | !(n ^ 262144) * 18
     | !(n ^ 131072) * 17
     | !(n ^ 65536) * 16
     | !(n ^ 32768) * 15
     | !(n ^ 16384) * 14
     | !(n ^ 8192) * 13
     | !(n ^ 4096) * 12
     | !(n ^ 2048) * 11
     | !(n ^ 1024) * 10
     | !(n ^ 512) * 9
     | !(n ^ 256) * 8
     | !(n ^ 128) * 7
     | !(n ^ 64) * 6
     | !(n ^ 32) * 5
     | !(n ^ 16) * 4
     | !(n ^ 8) * 3
     | !(n ^ 4) * 2
     | !(n ^ 2);
}

int main() {
  for (int i=1; i<1048577; i <<= 1){
    cout << f(i) << " "; // 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20
  }
}

- גלעד ברקן