我看到很多问题告诉你如何解决这个问题,但没有一个真正解释了发生了什么,除了“浮点舍入误差很糟糕”。所以让我来试一下。首先,让我指出,
这个答案中没有任何特定于Java的内容。舍入误差是固定精度表示数字所固有的问题,因此在C等语言中也会出现相同的问题。
十进制数据类型中的舍入误差
作为一个简化的例子,想象一下我们有一种计算机,它本地使用无符号的十进制数据类型,让我们称其为float6d。数据类型的长度为6位数字:4位用于尾数,2位用于指数。例如,数字3.142可以表示为
3.142 x 10^0
这将被存储为6位数字
503142
前两位是指数加50,后四位是尾数。这种数据类型可以表示从0.001 x 10^-50到9.999 x 10^+49之间的任何数字。
实际上,那并不是真的。如果你想要表示3.141592?或者3.1412034?或者3.141488906?很遗憾,这种数据类型不能存储超过四位精度的数字,所以编译器必须将具有更多数字的任何内容舍入以适应数据类型的限制。如果你写
float6d x = 3.141592;
float6d y = 3.1412034;
float6d z = 3.141488906;
然后编译器将这三个值转换为相同的内部表示形式,即
3.142 x 10^0(记住,它存储为
503142),因此
x == y == z成立。
关键在于,有一整个实数范围映射到相同的底层数字序列(或在实际计算机中为位)。具体而言,任何满足3.1415 <= x <= 3.1425(假设使用“半偶数”舍入)的x都会被转换为表示为503142以在内存中存储。
每次程序将浮点数值存储在内存中时,都会进行此舍入。第一次发生的时间是当您在源代码中写入常量时,就像我上面使用x、y和z一样。每当执行增加数据类型所能表示的精度位数的算术运算时,它都会再次发生。这两种效果之一称为舍入误差。这可能会以几种不同的方式发生:
Addition and subtraction: if one of the values you're adding has a different exponent from the other, you will wind up with extra digits of precision, and if there are enough of them, the least significant ones will need to be dropped. For example, 2.718 and 121.0 are both values that can be exactly represented in the float6d data type. But if you try to add them together:
1.210 x 10^2
+ 0.02718 x 10^2
1.23718 x 10^2
which gets rounded off to 1.237 x 10^2, or 123.7, dropping two digits of precision.
Multiplication: the number of digits in the result is approximately the sum of the number of digits in the two operands. This will produce some amount of roundoff error, if your operands already have many significant digits. For example, 121 x 2.718 gives you
1.210 x 10^2
x 0.02718 x 10^2
3.28878 x 10^2
which gets rounded off to 3.289 x 10^2, or 328.9, again dropping two digits of precision.
However, it's useful to keep in mind that, if your operands are "nice" numbers, without many significant digits, the floating-point format can probably represent the result exactly, so you don't have to deal with roundoff error. For example, 2.3 x 140 gives
1.40 x 10^2
x 0.23 x 10^2
3.22 x 10^2
which has no roundoff problems.
Division: this is where things get messy. Division will pretty much always result in some amount of roundoff error unless the number you're dividing by happens to be a power of the base (in which case the division is just a digit shift, or bit shift in binary). As an example, take two very simple numbers, 3 and 7, divide them, and you get
3. x 10^0
/ 7. x 10^0
----------------------------
0.428571428571... x 10^0
The closest value to this number which can be represented as a float6d is 4.286 x 10^-1, or 0.4286, which distinctly differs from the exact result.
作为下一节中我们将看到的,由四舍五入引入的误差随着每次操作而增加。因此,如果您使用的是“好”数字(如您的示例),通常最好尽可能晚地进行除法运算,因为这些运算最有可能在程序中引入舍入误差。
舍入误差分析
一般来说,如果您不能假设您的数字是“好”的,则舍入误差可能是正的或负的,并且很难根据操作预测它将朝哪个方向发展。它取决于涉及的具体值。看一下这个以
float6d数据类型为例的
2.718 z的舍入误差随着
z变化的图表:
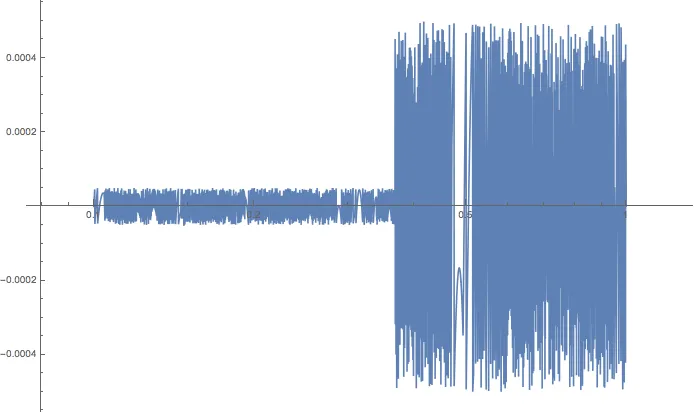
实际上,当您使用数据类型的全精度值时,将舍入误差视为随机误差通常更容易。从图中可以看出,您可能能够猜测误差的大小取决于操作结果的数量级。在这种特定情况下,当
z 的数量级为 10
-1 时,
2.718 z 也是数量级为 10
-1 的数字,因此它将成为形式为
0.XXXX 的数字。最大舍入误差然后是精度的最后一位数字的一半;在这种情况下,我指的是 0.0001 的“精度的最后一位数字”,因此舍入误差在 -0.00005 和 +0.00005 之间变化。在
2.718 z 跳到下一个数量级(即 1/2.718 = 0.3679)的点上,您可以看到舍入误差也会跳一个数量级。
你可以使用众所周知的
误差分析技术 来分析某个大小的随机(或不可预测)误差如何影响你的结果。具体而言,对于乘法或除法,你的结果中的“平均”相对误差可以通过将每个操作数的相对误差
平方 - 即将它们平方、相加并取平方根来近似计算。使用我们的
float6d 数据类型,相对误差在 0.0005(例如 0.101)和 0.00005(例如 0.995)之间变化。
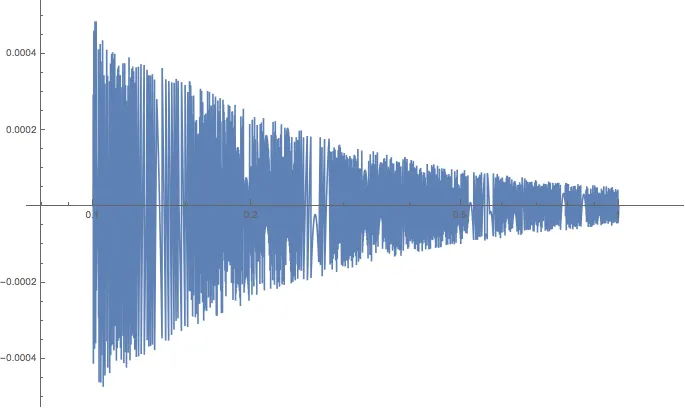
让我们将0.0001作为值x和y的相对误差的粗略平均值。则x * y或x / y的相对误差由以下公式给出:
sqrt(0.0001^2 + 0.0001^2) = 0.0001414
这个因子比每个单独值的相对误差大sqrt(2)倍。
当涉及到多个操作时,您可以为每个浮点运算应用此公式多次。例如,对于z / (x * y),x * y的相对误差平均为0.0001414(在此十进制示例中),然后z / (x * y)的相对误差为
sqrt(0.0001^2 + 0.0001414^2) = 0.0001732
注意,平均相对误差随每次操作增加而增加,具体地说,它随你执行的乘除运算数量的平方根增长。
同样地,在
z / x * y 中,
z / x 的平均相对误差为 0.0001414,
z / x * y 的相对误差为。
sqrt(0.0001414^2 + 0.0001^2) = 0.0001732
所以,在这种情况下是一样的。这意味着
对于任意值,平均而言,两个表达式引入的误差大约相同。(理论上是这样。我见过这些操作在实践中表现非常不同,但那是另一回事。)
详细信息
您可能对问题中提出的具体计算感到好奇,而不仅仅是一个平均值。为了进行分析,让我们转到二进制算术的真实世界。在大多数系统和语言中,浮点数使用IEEE标准754进行表示。对于64位数字,格式指定52位专用于尾数,11位专用于指数,1位专用于符号。换句话说,当以2为底写成浮点数时,其形式为:
1.1100000000000000000000000000000000000000000000000000 x 2^00000000010
52 bits 11 bits
前导的1没有明确存储,它构成了第53位。此外,您应该注意,用于表示指数的11位实际上是真实指数加1023。例如,这个特定的值是7,即1.75 x 22。尾数是二进制下的1.75,或者1.11,指数是1023 + 2 = 1025,二进制下为10000000001,因此存储在内存中的内容为
01000000000111100000000000000000000000000000000000000000000000000
^ ^
exponent mantissa
但这并不重要。
你的例子还涉及450。
1.1100001000000000000000000000000000000000000000000000 x 2^00000001000
和60,
1.1110000000000000000000000000000000000000000000000000 x 2^00000000101
你可以使用
此转换器或互联网上的其他许多转换器来尝试这些值。
当您计算第一个表达式
450/(7*60)时,处理器首先进行乘法运算,得到420。
1.1010010000000000000000000000000000000000000000000000 x 2^00000001000
然后它将450除以420,得到15/14。
1.0001001001001001001001001001001001001001001001001001001001001001001001...
在二进制下。现在,Java语言规范指出:
不精确的结果必须舍入为最接近无穷精确结果的可表示值;如果两个最接近的可表示值同样接近,则选择其最低有效位为零的值。这是IEEE 754标准的默认舍入模式,称为四舍五入至最近。
在64位IEEE 754格式中,15/14的最近可表示值为
1.0001001001001001001001001001001001001001001001001001 x 2^00000000000
这段文字涉及编程相关内容。第一段文字中的数字
1.0714285714285714 在十进制下约等于 1.0714285714285714,更准确地说,这是最不精确的十进制值,可以唯一确定该特定二进制表示法。另一方面,如果首先计算 450 / 7,则结果为 64.2857142857...,或用二进制表示为:
1000000.01001001001001001001001001001001001001001001001001001001001001001...
最接近的可表示值为
1.0000000100100100100100100100100100100100100100100101 x 2^00000000110
这是64.28571428571429180465... 注意到二进制尾数的最后一位(与精确值相比)由于舍入误差而发生了变化。将其除以60即可得到
1.000100100100100100100100100100100100100100100100100110011001100110011...
看一下结尾:模式不同了!重复的是0011,而不是另一种情况下的001。最接近可表示的值为
1.0001001001001001001001001001001001001001001001001010 x 2^00000000000
这与最后两位的其他运算顺序不同:它们是10而不是01。十进制等效值为1.0714285714285716。
如果您查看确切的二进制值,应该可以清楚地看到导致此差异的特定舍入:
1.0001001001001001001001001001001001001001001001001001001001001001001001...
1.0001001001001001001001001001001001001001001001001001100110011001100110...
^ last bit of mantissa
在这种情况下,前面的结果数值上为15/14恰好是最准确的表示。这是一个将除法留到最后的好处的例子。但是,只要你处理的值没有使用数据类型的完整精度,这个规则才能保持有效。一旦你开始使用不精确(四舍五入)的值,通过先进行乘法运算就不能再保护自己免受进一步的舍入误差的影响了。


450.00d / (420d)(在计算7d * 60的第一步中没有精度损失)。第二行首先计算450.00d / 7d并存储结果,由于计算机存储浮点数的方式,这一步会有少量精度损失,然后将该结果除以 60。您可以在此处了解浮点数的工作原理:http://floating-point-gui.de/formats/fp/ - Nils O