根据Oli Charlesworth的说法,你可以构建一个DFA,用于判断基数为b的数能否被某个除数d整除,其中DFA中的状态表示除法的余数。
对于您的情况(基数为2 - 二进制数,除数d= 310):
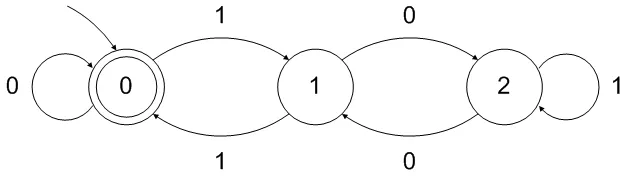
请注意,上面的DFA接受空字符串作为可被3整除的“数字”。这很容易通过在前面添加一个中间状态来修复:
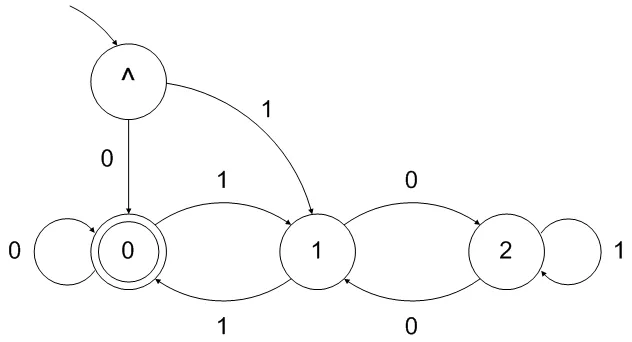
将其转换为理论正则表达式可以使用常规过程完成。
一旦你得到了DFA,就可以在支持递归正则表达式的实现中轻松地将其转换为实际的正则表达式。这在(基数b= 10,d = 710)的情况下在CodeGolf.SE的这个问题中有所展示。
让我引用Lowjacker答案中的正则表达式, 它采用了Ruby正则表达式风格:
(?!$)(?>(|(?<B>4\g<A>|5\g<B>|6\g<C>|[07]\g<D>|[18]\g<E>|[29]\g<F>|3\g<G>))(|(?<C>[18]\g<A>|[29]\g<B>|3\g<C>|4\g<D>|5\g<E>|6\g<F>|[07]\g<G>))(|(?<D>5\g<A>|6\g<B>|[07]\g<C>|[18]\g<D>|[29]\g<E>|3\g<F>|4\g<G>))(|(?<E>[29]\g<A>|3\g<B>|4\g<C>|5\g<D>|6\g<E>|[07]\g<F>|[18]\g<G>))(|(?<F>6\g<A>|[07]\g<B>|[18]\g<C>|[29]\g<D>|3\g<E>|4\g<F>|5\g<G>))(|(?<G>3\g<A>|4\g<B>|5\g<C>|6\g<D>|[07]\g<E>|[18]\g<F>|[29]\g<G>)))(?<A>$|[07]\g<A>|[18]\g<B>|[29]\g<C>|3\g<D>|4\g<E>|5\g<F>|6\g<G>)
分解一下,你可以看到它是如何构建的。使用 原子 分组(或 非回溯 分组,或行为类似于 占有性)来确保仅匹配空字符串选项。这是模拟 Perl 中的 (?DEFINE) 的技巧。然后,组 A 到 G 对应于将该数字除以 7 的余数为 0 到 6 的部分。
(?!$)
(?>
(|(?<B>4 \g<A>|5 \g<B>|6 \g<C>|[07]\g<D>|[18]\g<E>|[29]\g<F>|3 \g<G>))
(|(?<C>[18]\g<A>|[29]\g<B>|3 \g<C>|4 \g<D>|5 \g<E>|6 \g<F>|[07]\g<G>))
(|(?<D>5 \g<A>|6 \g<B>|[07]\g<C>|[18]\g<D>|[29]\g<E>|3 \g<F>|4 \g<G>))
(|(?<E>[29]\g<A>|3 \g<B>|4 \g<C>|5 \g<D>|6 \g<E>|[07]\g<F>|[18]\g<G>))
(|(?<F>6 \g<A>|[07]\g<B>|[18]\g<C>|[29]\g<D>|3 \g<E>|4 \g<F>|5 \g<G>))
(|(?<G>3 \g<A>|4 \g<B>|5 \g<C>|6 \g<D>|[07]\g<E>|[18]\g<F>|[29]\g<G>))
)
(?<A>$| [07]\g<A>|[18]\g<B>|[29]\g<C>|3 \g<D>|4 \g<E>|5 \g<F>|6 \g<G>)


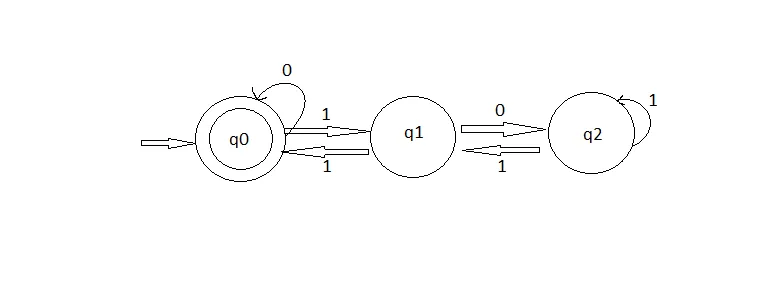 注意:边缘
注意:边缘