给定四个正整数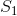 ,
, 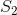 ,
, 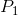 和
和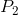 ,是否有一种快速找到任意两个整数
,是否有一种快速找到任意两个整数 和
和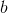 的方法,使得:
的方法,使得:
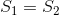 和
和 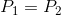 时,使用二次方程式可以得到一个闭合形式的
时,使用二次方程式可以得到一个闭合形式的 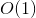 解决方案。我们只需找到
解决方案。我们只需找到 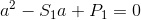 的根,就能得到一个适当的
的根,就能得到一个适当的  。
。
当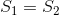 时,我知道如何通过注意到曲线
时,我知道如何通过注意到曲线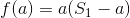 是凸的,所以我们可以二分搜索适当的
是凸的,所以我们可以二分搜索适当的 ,从而在
,从而在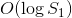 中解决它。
中解决它。
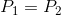 时,可以通过对
时,可以通过对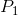 进行因式分解,并查找在范围内求和的一对因子来解决
进行因式分解,并查找在范围内求和的一对因子来解决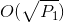 。请注意保留HTML标记。
。请注意保留HTML标记。
然而,当两个都是范围时,我想不出任何可以高效解决此问题的算法。有一些可能的启发式方法,比如固定其中一个(遍历较小的范围等),或者在两个整数之和为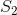 时可以制造的最大可能乘积小于
时可以制造的最大可能乘积小于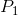 时立即报告不存在任何一对等。
时立即报告不存在任何一对等。
很遗憾,我还没有想出任何比迭代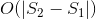 或
或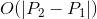 (可能带有一些额外的小因子)更快的通用解决方案。是否有一种好的算法或一些花哨的数学方法可以提供更快的解决方案?
(可能带有一些额外的小因子)更快的通用解决方案。是否有一种好的算法或一些花哨的数学方法可以提供更快的解决方案?
另外,是否有一种方法可以证明迭代会迅速终止?(在处理一些边缘情况等之后。)我不关心有效对数的数量;找到任何一对即可。如果允许的总和范围足够大,则迭代乘积并尝试找到相应的总和似乎很快就能找到解决方案。这是否可能有某种证明呢?
我非常感谢任何帮助!
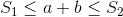
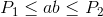
S1、S2、P1和P2的范围有限制吗?例如,如果它们都是严格正数,那么解决起来应该比一般情况更容易,因为例如a和b都不能大于或等于S2或P2。因此,搜索范围限制为1..min(S2, P2)。 - twalbergmax(S1 - b, P1/b) <= a <= min(S2 - b, P2/b)。也许描述这个不等式可以帮助找到 O(1) 的解决方案。 - darksky