logo标签列表

从给定的数字中，确定三个接近的数字，使它们的乘积等于原始数字。

algorithmmathlanguage-agnosticnumbers
26

我有一个数字n，我想找到三个数，它们的乘积是n，但彼此之间尽可能接近。也就是说，如果n = 12，那么我希望得到3、2、2作为结果，而不是6、1、2。

另一种思考方式是，如果n是一个长方体的体积，那么我想找到边长，使得长方体尽可能地像一个立方体（即，长度尽可能相似）。这些数字必须是整数。

我知道这个问题不太可能有完美的解决方案，我很乐意使用大多数情况下能给出好答案的方法，但我不知道该如何设计这个算法。有什么建议吗？

3
三个数字之间的距离有什么衡量标准？ - Phonon
6
如果n在1到50之间，为什么不预先计算结果呢？ - Nick Johnson
2
你需要清楚地定义“尽可能接近”的含义。提出一个方程，然后选择你最喜欢的优化方法。 - job
2
编写一个函数，它可以说明解决方案的好坏，并使用n的质因数分解进行暴力破解。对于这样小的n，这不应该是一个问题。 - akappa
2
@user207442：最小的反例是24，你的解决方案是（2,2,6），但（2,3,4）更好。对于120，你得到（2,6,10），而（4,5,6）更好。尽可能选择彼此接近的数字通常不会有公共因数，除非它们相等 :-) - Steve Jessop
显示剩余11条评论
5个回答
12

这是我的第一个算法草稿，假设n相对较小：

  • 计算n的质因数。
  • 挑选出最大的三个质因数并将它们分配给f1，f2，f3。如果小于三个因子，则分配1。
  • 按递减顺序循环剩余的因子，将它们乘入当前最小的分区。

编辑

让我们以n=60为例。

它的质因数是5 3 2 2。

设置f1=5，f2=3和f3=2。

剩下的2被乘到f3中，因为它是最小的。

我们最终得到5 * 4 * 3 = 60。

编辑

请注意，此算法将不会找到最优解，参见btilly的评论：

考虑17550 = 2 * 3 * 3 * 3 * 5 * 5 * 13。您的算法会给出15、30、39，而最佳答案是25、26、27。

编辑

好的，这是我的第二个算法草稿，带有稍微更好的启发式：

  • 将列表L设置为n的质因数。
  • 将r设置为n的立方根。
  • 创建三个因子的集合F，最初设置为1。
  • 按降序迭代质因数：
    • 尝试将当前因子L[i]与每个因子按降序相乘。
      • 如果结果小于r，则执行乘法并继续下一个质因数。
      • 否则，尝试下一个F。如果超出F，则乘以最小的。

对于17550的情况，这将起作用：

n=17550
L=13,5,5,3,3,3,2
r=25.98

F = { 1, 1, 1 }

迭代1：

  • 如果F[0] * 13小于r，则将F设置为{13,1,1}。

迭代2：

  • F[0] * 5 = 65大于r。
  • 如果F[1] * 5小于r，则将F设置为{13,5,1}。

迭代3：

  • F[0] * 5 = 65大于r。
  • 如果F[1] * 5小于r，则将F设置为{13,25,1}。

迭代4：

  • F[0] * 3 = 39大于r。
  • F[1] * 3 = 75大于r。
  • 如果F[2] * 3小于r，则将F设置为{13,25,3}。

迭代5：

  • F[0] * 3 = 39大于r。
  • F[1] * 3 = 75大于r。
  • 如果F[2] * 3小于r，则将F设置为{13,25,9}。

迭代6：

  • F[0] * 3 = 39大于r。
  • F[1] * 3 = 75大于r。
  • F[2] * 3 = 27大于r，但它是我们能得到的最小的F。将F设置为{13,25,27}。

迭代7：

  • F[0] * 2 = 26大于r，但它是我们能得到的最小的F。将F设置为{26,25,27}。
我喜欢这个，尽管我不认为这总能给出最好的答案。从质因数分解开始是一个很好的开始方式。 - Justin
@Anders - 这非常好。我正在尝试找到一种它无法处理的情况，但只要我按递减顺序“循环剩余因子”，这并不那么容易。 - Justin
3
考虑 17550 = 2 * 3 * 3 * 3 * 5 * 5 * 13。你的算法会给出15、30和39，而正确答案是25、26和27。请修改算法以得到正确答案。 - btilly
1
@Anders，你的算法对于数字68、318、1098会得出什么结果？如果我编码正确，我得到的是{1, 4, 17}、{1, 6, 53}和{2, 9, 61}，但我认为{2, 2, 17}、{2, 3, 53}和{3, 6, 61}更好。 - Mr.Wizard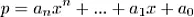
1
@Anders：对于你的第一次尝试算法，我给出+1的评价。它简单、快速且能够提供最优或接近最优的结果。 - ypercubeᵀᴹ
显示剩余10条评论
3
这里提供了一种纯数学方法，不需要排序，也不需要使用质因数，返回最优解。
背景：
1. 对于一个多项式
enter image description here 其根的和与积分别为
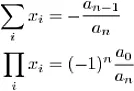enter image description here 其中 x_i 是根。
2. 回想一下优化理论中的另一个基本结果：
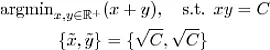enter image description here 即，给定两个变量，它们的乘积为常数时，当这两个变量相等时，它们的和是最小的。波浪线变量表示最优值。
由此可以得出一个推论，如果两个乘积为常数的变量之和最小，则这两个变量相等。
重新定义原问题：
现在，你的问题可以重新定义为多项式求根问题。我们将构造一个满足条件的多项式，其根将是答案。如果你需要 k 个最优数，你将需要一个 k 次多项式。在这种情况下，我们可以用一个三次方程来描述它。 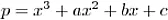enter image description here 我们知道：
1. c 是输入数的相反数（假设为正数）。 2. a 是负整数（因为因子都是正数）。 3. b 是整数（根据两个根之和），且为正数。 4. 多项式 p 的根必须是实数（并且是正数，但已经解决了这个问题）。
为了解决这个问题，我们只需要在上述条件下最大化 a。现在唯一不明确的部分是第四个条件，我们可以使用多项式的判别式轻松实现它。
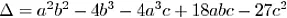对于一个三次多项式 p，其判别式为 enter image description here 如果 ∆>0，则 p 具有实且不同的根，如果 ∆=0，则 p 具有实且重复的根（其中两个或全部三个）。因此，约束条件 4 现在变成了 ∆>=0。这现在很简单，易于编程。

Mathematica解决方案

这是一个在Mathematica中实现的解决方案。

以下是对其他答案/评论中使用的一些数字进行测试的结果。

enter image description here

左侧列是列表，右侧列中的相应行给出了最佳解决方案。

注意：

我刚刚注意到OP从未提到需要三个数字是整数，尽管每个人（包括我自己）都假设它们是整数（可能是因为他的第一个例子）。重新阅读问题，并根据立方体示例，似乎OP并没有固定在整数上。

这是一个重要的问题，将决定要追求哪类算法，并需要定义。如果它们不需要是整数，则可以提供几种基于多项式的解决方案之一，其中之一是我的解决方案（放松整数约束后）。如果它们应该是整数，则可能使用分支和界限/分支和割平面的方法更合适。

以下内容是在假定OP意味着三个数字是整数的情况下编写的。

我目前实现的方式在某些情况下可以给出非整数解。

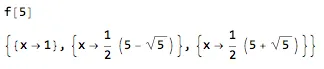
enter image description here

这会导致x的非整数解，因为我只最大化了a，实际上，b也需要最小化（不仅如此，还因为我没有对x_i是整数施加约束。可以使用“整数根定理”，它涉及到找到质因数，但会使事情变得更加复杂）。

Mathematica代码文本

Clear[poly, disc, f]
poly = x^3 + a x^2 + b x + c;
disc = Discriminant[poly, x];
f[n_Integer] := 
 Module[{p, \[CapitalDelta] = disc /. c -> -n}, 
  p = poly /. 
     Maximize[{a, \[CapitalDelta] >= 0, 
        b > 0 && a < 0 && {a, b} \[Element] Integers}, {a, b}][[
      2]] /. c -> -n;
  Solve[p == 0]
  ]
我并不完全相信这是 O(1)。你能否尝试使用 c=2*3*5*7*...*997 或 c=2*3*5*7*...*999983 来测试一下，告诉我们它的执行速度如何？ - ypercubeᵀᴹ
1
@ypercube：它不必是0<b<c或-c<a<0；例如，考虑n=2。三个最优数是1,1,2，其中a=-4，b=5，c=2。代码的中心部分就是这样：最大化a，使得a为负整数，b为正整数且判别式∆为非负数。一旦找到a和b，则将其代入原多项式并找到其根。 - user616736
Yoda，当您发布Mathematica代码的图片时，请至少在“输入图像描述”框中包含代码本身。 - Mr.Wizard
@ypercube：问题是NP难的，所以我认为不可能找到一个简单的多项式解决方案，适用于每个“n”。 - user616736
@Mr. Wizard：完成了。我发现如果您在“输入图像描述”框中输入，它不起作用，因为mma括号会干扰。 - user616736
显示剩余3条评论
2

可能有一种聪明的方法来找到最紧密的三元组，就像Anders Lindahl正在追求的那样，但我将专注于更基本的方法。

如果我生成所有三元组，然后可以按照自己的需求进行过滤，所以我将从那里开始。我知道生成这些的最好方法是使用递归：

f[n_, 1] := {{n}}

f[n_, k_] := Join @@
    Table[
      {q, ##} & @@@ Select[f[n/q, k - 1], #[[1]] >= q &],
      {q, #[[2 ;; ⌈ Length@#/k ⌉ ]] & @ Divisors @ n}
    ]

这个函数f有两个整数参数，一个是要分解的数字n，另一个是需要生成的因子数量k。

代码段#[[2 ;; ⌈ Length@#/k ⌉ ]] & @ Divisors @ n使用Divisors生成n的所有因数（包括1）的列表，然后从第二个开始（去掉1），到除以k所得因数数量向上取整的位置。

例如，对于{n = 240, k = 3}，输出结果为{2, 3, 4, 5, 6, 8}

Table命令在迭代列表时累积结果，并将每个元素分配给q。

Select[f[n/q, k - 1], #[[1]] >= q &]是Table的主体。它递归调用f，然后从结果中选择以>= q开头的所有列表。

{q, ##} & @@@（也在主体中）然后在这些选定的列表的每个循环中“前置”q。

最后，Join @@合并由Table的每个循环产生的这些选定列表的列表。

结果是将n的所有整数因子分成k部分，按字典顺序排列。例如：

In[]:= f[240, 3]

Out[]= {{2, 2, 60}, {2, 3, 40}, {2, 4, 30}, {2, 5, 24}, {2, 6, 20},
        {2, 8, 15}, {2, 10, 12}, {3, 4, 20}, {3, 5, 16}, {3, 8, 10},
        {4, 4, 15}, {4, 5, 12}, {4, 6, 10}, {5, 6, 8}}

使用上述函数/算法的输出，可以根据需要测试三元组的质量。
请注意，由于排序，输出中的最后一个三元组是具有最大最小因子的三元组。这通常是结果中最 "立方体" 的，但偶尔不是。
如果必须找到真正的最优解，那么从列表的右侧开始测试是有意义的，如果没有快速找到更好的结果，则放弃搜索，因为随着向左移动，结果的质量会降低。
很明显，这种方法依赖于快速的Divisors函数，但我认为这要么是一个标准库函数，要么您可以在StackOverflow上找到一个好的实现。有了这个功能，它应该非常快。上面的代码在我的机器上找到1到10,000的所有三元组，在1.26秒内完成。
W +1 你的方法是一种非常非常高效的方法来计算除数的三元组。但是你仍然需要决定哪个三元组最接近立方体。如果我们将你的方法与我提出的最短空间对角线标准结合起来，那么我们将能够迅速完整地解决这个挑战，你觉得呢？ - DavidC
@David 我也希望如此。顺便问一下，为什么对角线要优于最大因数与最小因数之比呢？ - Mr.Wizard
（终于）我的偏好更多是情感上的而非理性上的。从经验上来看，它们往往会给出相同的解决方案。 - DavidC
1

不要重复造轮子，应该将其视为一个众所周知的NP完全问题的变体。

  • 计算n的质因数。
  • 计算这些因数的对数
  • 该问题可以转化为将这些对数分成三个尽可能接近的和。
  • 这个问题被称为装箱问题的一个变体，也被称为多处理器调度

考虑到多处理器调度问题是NP完全问题，很难找到一种不搜索整个问题空间并找到最优解的算法。

但我想已经有几种算法处理了装箱或多处理器调度，并以有效的方式找到了接近最优解。

另一个相关的问题（泛化）是作业车间调度。请参阅维基百科的描述，其中包含许多已知算法的链接。

维基百科所描述的（常用的LPT算法（最长处理时间）正是Anders Lindahl最先提出的。

你打算如何处理质因数的对数？ - DavidC
1
你是在说这个问题是NP完全的吗？我给你提供了一个Bin Packing问题的实例。同时，我也允许你调用我的oracle立方体积最小化器，它可以在多项式时间内解决任何一个立方体积最小化问题的实例。那么你如何在多项式时间内解决这个Bin Packing问题呢？ - Rob Neuhaus
1

编辑 这里有一个更简洁的解释，使用了更高效的代码，KSetPartitions 大大简化了事情。Mr.W 的一些建议也起到了作用。总体逻辑保持不变。

假设 n 至少有 3 个质因数，

  1. 找到 n 的质因数的三元组 KSetPartitions 列表。
  2. 将每个子集中的每个元素（质因数）相乘，以产生 n 的三个约数的所有可能组合（当它们相乘时，它们产生 n）。您可以将约数视为正交平行六面体的长度、宽度和高度。
  3. 最接近立方体的平行六面体将具有最短的空间对角线。对于每种情况，求出三个约数的平方和并选择最小值。

以下是在Mathematica中的代码：

Needs["Combinatorica`"]
g[n_] := Module[{factors = Join @@ ConstantArray @@@ FactorInteger[n]},
  Sort[Union[Sort /@ Apply[Times, Union[Sort /@ 
      KSetPartitions[factors, 3]], {2}]] 
      /. {a_Integer, b_Integer, c_Integer} :>  
           {Total[Power[{a, b, c}, 2]], {a, b, c}}][[1, 2]]]

它可以处理相当大的数字，但随着 n 的因子数量增加，速度会显著减慢。下面的示例显示了240、2400、... 24000000的计时情况。 原则上，这可以通过考虑除数中一个质因数出现多次的情况来加快速度。但目前我还不具备相关技术知识。

In[28]:= g[240]

Out[28]= {5, 6, 8}

In[27]:= t = Table[Timing[g[24*10^n]][[1]], {n, 6}]

Out[27]= {0.001868, 0.012734, 0.102968, 1.02469, 10.4816, 105.444}
@Mr. W 非常感谢您的帮助。我对这种方法的逻辑感到异常乐观，尽管它有点贪心。听到您提出的效率改进措施将会很有趣。您总是能做到最好的。 - DavidC
David，你太好了。我会尽快发布解决方案，但我有些事情要忙。首先，我想看看Anders Lindahl是否对我的问题/批评有回应，因为我认为他的方法可能是最快的，如果能正确地运行（或已经运行），而我只是编码错误。 - Mr.Wizard
与此同时，让我提出一些我认为可以在您的代码中改进的事情（我会稍后考虑方法）。(1) Flatten[FactorInteger[n] /. {a_Integer, b_Integer} :> Table[a, {b}]] 应该被替换为 Join @@ ConstantArray @@@ FactorInteger@n (2) 我认为 Sqrt 是多余的 (3) 最好一次将所有数字平方，因为 Power 是 Listable 并且使用 Total 相加比使用规则 {a_, b_, c_} :> ... 处理每个三元组更快 (4) SortBy 应该比您正在使用的装饰和排序方法更快 - Mr.Wizard
(5) 你的装饰和排序速度很慢，因为你正在使用自定义排序函数；将每个子列表中的“排序”元素放在第一位，并使用默认的Sort。 (6) 生成所有集合分区非常低效。好了，我想这应该足够攻击你的代码了。 :o) - Mr.Wizard
这有很大的改进。KSetPartitions 仍然不是最优的，因为它会出现重复（这些重复被 Union 去除）。这并没有更快，但代码更加简洁: g2[n_] := Module[{factors = Join @@ ConstantArray @@@ FactorInteger[n]}, SortBy[ Union[ Sort /@ Apply[Times, Union[Sort /@ KSetPartitions[factors, 3]], {2}]], Total[#^2] & ][[1]] ] - Mr.Wizard
显示剩余6条评论
网页内容由stack overflow 提供, 点击上面的
可以查看英文原文，
原文链接